Well-known algorithms Flashcards
(15 cards)
What is the BUILD-MAX-HEAP run-time?
O(n)
- n-element heap has height O(log(n))
- At most [n/2^(h+1)] nodes of any height h
- Max-Heapify on a node of height h - O(h)
Thus, the run-time is bounded by.. (image)

What does MAX-HEAPIFY and what is its run-time?
Run-time: O(logn)
MAX-HEAP-INSERT, HEAP-EXTRACT-MAX
O(logn)
What is HEAP-INCREASE-KEY and what’s its run-time?
O(logn)
Describe the implementation of BFS(G,s) and analyze its run-time.
Run-time:
- Init - O(V)
- loop over all vertices, dealing with every edge only once - O(V + E)
In total: O(V+E)
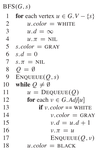
Depth-First-Search implementation and run-time
- Run-time: O(V+E)*
- We traverse each vertex once and each edge at most once*

- What is a topological sort?*
- When it can’t be implemented?*
- How is it implemented?*
What’s its run-time?
- It is a linear ordering of a graph such that if G contains an edge (u,v) then u appears before v in the ordering.*
- Can’t be implemented if there are cycles in G.*
- Run-time: O(V+E) (just as BFS)*
- What are the properties of a tree G=(V,E)?*
- (there are 5)*
Tree is a connected,acylic,undirected graph
- Any two vertices in G are connected*
- G is connected, but if any edge is removed from E, the resulting graph is disconnected*
- G is connected, and |E| = |V|-1*
- G is acylic, and |E| = |V|-1*
- G is acyclic, but if any edge is added to E, the resulting graph contains a cycle.*
What is a rooted tree?
- A rooted tree is a tree in which one of the vertices is distinguished from the others - the root.*
- We often call a vertex in a rooted tree a node.*
- Consider a node x in a rooted tree T with root r:*
- A node y on the unique path from r to x is called an ancestor.
- y = ancestor(x) <==> x=descendat(y)
- For every node x, x=ancestor(x)=ancestor(y)
- y is a proper ancestor if, y = ancestor(x) and y!=x
- x is a proper descendant if, x = descendant (y) and x!=y
- The subtree rooted at x is the tree induced by descendants of x, rooted at x.
- If the last edge on the simple path from the root r of a tree T to a node x is (y,x) then y is the parent of x, and x is a child of y.
- The root is the only node with no parent.
- Node with no children is a leaf
- Node that has children is an internal node
- two node, same parent - siblings
- Degree(x) = node x’s number of children
- depth(x) = length of Prx, where r is the root.
- Level - all nodes at the same depth.
- Height(x)- longest path from x to some leaf
- Height(T) - height of its root/largest depth
What is an ordered-tree?
It is a rooted tree in which the children of each node are distinguished.
Describe Bucket-Sort’s main points.
- Depends on property of the input, therefore stand on an average run-time of O(n).*
- Property:*
- Having n elements in the input, the input is evently distributed between the intervals [0,1/n), [1/n,2/n),… , [(n-1)/n, 1)
It does that by shifting each element to the set which fits it, then sorting each set using insertion set and eventually combining them all.
The main idea is that insertion sort take O(ni^2) but because the elements are evenly distributed, O(n1^2 + n2^2 + … + nn^2) = O(n).
Describe Radix Sort’s main points
- Given n d-digits numbers, in which each digit can take up to k possible values, Radix sorts the least significant digit first, in a stable manner, until it reaches the most significant.*
- Because we know that each “column” is bloced by k, we can sort each column in O(n+k)*
- given n d-digit numbers in which each digit can take on up to k possible values, Radix-Sort correctly sorts these numbers in O(d(n+k)) time if the stable sort it uses take O(n+k)*
- given n b-bit numbers and any positive interger r<=b, Radix-Sort correctly sorts these numbers in O((b/r)(n+2^r)) time if the stable sort it uses takes O(n+k) time for inputs in the range 0 to k.*
Describe Counting-Sort’s algorithm and run-time
Counting sort is based on a preknowledge about the input - the n given numbers are bounded by some integer k.
This inforamtion enables sorting in O(n+k)
Describe priority queue
A priority queue is a data structure for maintaining a set of S elements, each with an associated value called a key. A max-priority queue supports the following operations:
- Insert(S,x)
- Maximum(S) - return max element
- Extract-Max(S) - extract max element
- Increase-Key(S)
Describe Disjoint-Set and its operations
A disjoint-set data structure maintains a collection S = {S1, S2 , … , Sk} of disjoint dynamic sets. we identify each set by a representative.
Assume S is composed of elements from V
Operations:
- MAKE-SET(x) - create a new set whose only member is x. NOTE: x is not found in any other set.
- UNION(x,y) - unite x and y and determine a new representative.
- FIND-SET(x) - return a pointer to the representative of the unique set containing x.
With the best implementation:
A sequence of m Make-Set, Union and FInd-Set operations, n of which are Make-Set operations take: O(m*a(n)), where a(n) is a very slowly growing function , a(4)<=4. Thus, we can view the running time as linear in m in all practical situations.


