Shortest paths algorithms Flashcards
(72 cards)
1
Q
What is the generic algorithm for finding delta(s,v) for all v’s?
A
Init:
- d(s)=0, d(v)=infinity
loop:
-
while (exists an edge (u,v) for which d(v)>d(u)+w(u,v):
- find such an edge and call Relax(u,v,w)
end:
- return d(v) for every v
2
Q
Lower bound claim
All along the run of the algorithm, for all v, the inequality: d(v)>=delta(s,v) is satisfied, and if d(v)
proof that claim.
A
Using induction on the number of Relax operations
-
base: after initilization
- v is not s, delta(s,v)
- d(s)=0 = delta(s,s)
-
Induction assumption
- by the end of the i-1 step, the assumption is satisfied.
-
step
- Let’s look at Relax on the ith step.
-
case 1: no update
- array d stays the same
-
case 2: updated
- d(v)-the only one that has changed.
- d(v)=d(u)+w(u,v)
- d(u)>=delta(s,u) (by I.A)
-
delta(s,u)+w(u,v) >= delta(s,v)
- observation.
- d(v)>= delta(s,u)+w(u,v)>=delta(s,v)
-
since d(v) is updated:
- d(v)
- d(u) - a weight of some Psu.
- d(v)=d(u)+w(u,v)*-**weight of Psu+(u,v)*
3
Q
What is the correctness statement for the generic algorithm?
A
If through the run of the algorithm, for every edge (u,v), d(v)<=d(u)+w(u,v) is satisfied(that is, the algorith, stops), then, for every v, d(v)=delta(s,v).
4
Q
What is the correctness statement proof for the generic algorithm, in case it stops?
A
-
Assume the algorithm stopped
- for all (u,v) in E, d(v)<=d(u)+w(u,v)
-
Assume in negation: there exists x in V s.t:
- d(x) != delta(s,x)
- Let Psx the lightest path from s to x.
-
let v be the first vertex in P s.t. d(v) != delta(s,v)
- by the lower bound claim: d(v)>delta(s,v)
-
let u be the preceding vertex to v in P
- d(u) = delta(s,u)
-
By sub-paths of a shortests path prinicipal
- delta(s,u)+w(u,v)=delta(s,v).
-
d(v)<=d(u)+w(u,v)=delta(s,u)+w(u,v)=delta(s,v)
- contradiction
5
Q
What is the “full” correctness statement of the generic algorithm?
A
6
Q
What is the exact definition of
rooted tree in vertex s
A
Directed graph is called rooted tree in vertex s if every vertex in the graph is accessible from s, and it is accessible only via one path
7
Q
Which data structure can help us maintain a rooted tree in vertex s?
A
It can be maintaind via array of length |V|
- The index of a cell represents some vertex*
- The content of cell v is former(v)*
8
Q
“lightest paths tree T for graph G and source s”
what is it?
A
It is a rooted tree in vertex s which satisfies:
for every v, the only path from s to v in T is the lightest path from s to v in G.
9
Q
General algorithm, what claims are used in order to prove the correctness statement?
A
10
Q
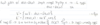
Generic algorithm, how the first claim is proved?
A
- N.T.F - d(u) = delta(s,u)
- lower bound claim - d(u)>=delta(s,u)
-
d(v)=d(u)+w(u,v) = delta(s,v)
- last Relax operation -> d(v)=delta(s,u)
- delta(s,v)<= delta(s,u)+w(u,v)
-
d(u)+w(u,v) = delta(s,v)<=delta(s,u)+w(u,v)
- d(u)<=delta(s,u)
-
d(u)>=delta(s,u) & d(u)<=delta(s,u)
- d(u) = delta(s,u)
11
Q
General algorithm, proof for the 2nd claim.
What is the induction based on
A
It is based on the size of V’. That is, |V’|.
12
Q
Genereal algorithm, proof of the 2nd claim.
What is the base case for the induction proof?
A
- |V’| = 1.*
That is:
- V’ = {s}
- E’ = empty set.
Trivial.
13
Q
- Generic algorithm, proof of the 2nd claim.*
- what is the step in the induction?*
A
- we look at the next vertex v to be added into V’. That is, the next vertex for which d(v) = delta(s,v).*
- N.T.S: T=(V’ U {v}, E’ U {former(v),v})* is a shortest paths tree.
14
Q
Generic algorithm, proof of the 2nd claim.
What is the proof for the step phase of the induction?
A
According to the 1st claim: d(v)=delta(s,v) means:
- former(v) = delta(s,former(v))
- therefore, former(v) is in V’ too.
Proof: T is a tree.
- (V’,E’) is a tree.
- former(v) is in V’
- we added an edge from former(v) to a new vertex v in V’.
proof: T is a shortest paths tree from s
- I.A holds for all other vertices. N.T.F for v.
-
The path Psv in T is composed of:
- Psformer(v) + (former(v),v)
- by the assumption: d(v)=delta(s,v)
- by claim 1: d(former(v)) = delta(s,former(v))
- w(Psv)=w(Psformer(v))+w(former(v),v) =
- delta(s,former(v))+w(fomer(v),v)=d(v) = delta(s,v)
15
Q
Generic algorithm, what is the proof for the correctness statement, using the claims.
A
- If the algorithm stops, then we proved that for all v, d(v) = delta(s,v) is satisfied.*
- Therefore, the Tree V’=V E’={(former(v),v): v!=s} can be created, and by the 2nd claim - G = (V’,E’) is a lightests paths tree from s in G.*.
16
Q
Dijstra, which graphs can it handle?
A
Directed or undirected graphs with non-negative weights.
17
Q
Dijstra, which problem can it solve?
A
Finding the shortest paths from source s to all vertices.
18
Q
_Dijstra, write exactly the Relax(u,v,w(u,v)) procedure_
A
19
Q
Dijstra, show me the initilization step.
You are given G=(V,E),s,w
A
20
Q
Dijstra, what is the loop step in the algorithm?
A
21
Q
How is Dijkstra’s algorithm implemented?
what’s his run-time? divide it to operation on Q and operations on the array d
A
- Q is maintained by a minimum heap in which d(v) is a key.*
- we push mininum d(v) from Q using ExtractMin.*
- Q*
- Initilization of Q - O(|V|)
- There are exactly |V| Extract-Min operations.
- There are at most |E| Relax operations, which decreases the value of d(v). This implies O(|E|) decrease-key(v) operations (log(|V|)). In total - O(|E|log|V|).
- d
- Initializing d and s - O(|V|)
- |E| Relax operations on d(v), each O(1). O(|E|)
- In total: O(|E|+|V|).
In total: O(|E| log|V|)
22
Q
Dijkstra, what is the lower bound claim?
A
d(v)>=delta(s,v)
That is, d(v) is always greater equal to the value of the lightest path.
23
Q
Dijkstra, What is the correctness statement?
A
When the algorithm is done, for all v, d(v)=delta(s,v)
24
Q
- Dijkstra, which observation is used in the proof?*
- Explain it.*
A
Once vertex u is being added to S, d(u) does not change.
Explanation:
- After u is being added to S, we execute Relax operation on vertex v from U, which share an edge with u. The updated value is d(v), and is again, is not chosen from S.
25
*Dijkstra, what is the first claim?*
*_Claim 1:_*
* *After Relax(u,v), _d(v)\<= d(u)+w(u,v)_ is satisfied through all the remaining steps of the algorithm.*
26
*_Diskjstra, what is the proof for the first claim?_*
By the end of Relax(u,v):
* d(v)=min{d(v),d(u)+w(u),v} is satisfied.
* That is, d(v)\<= d(u)+w(u,v)
* Relax is performed due to the insertion of u into S.
* According to the observation: d(u) will not further change.
* In contrast, d(v) might change, but only decrease, so the inequality holds.
27
*_Dijkstra, what is the helping statement?_*
*When vertex u is being added to S d(u)=delta(s,u) is satisfied.*
*_That is, d(u) holds the value for the lightest path_*
28
*Dijkstra, what is the proof for the correctness statement?*
*_Proof of the correctness statement_*
* *In each step a vertex shifts from Q to S*
* After |V| iterations, S=V and the algorithm stops.
* By the helping statement, when vertex u enters S:
* d(u) = delta(s,u)
* By the observation, this value does not change.
29
*Dijkstra, what is the proof for the helping statement?*
*We prove using induction on the algorithm steps - i:*
* *basis i = 1. when u=s.*
* *d(u) = 0*
* *delta(s,s) = 0*
* *Induction assumption:*
* *after i-1 iterations, for all u in S, d(u)=delta(s,u)*
* *step:*
* *let u be that ith vertex chosed to enter S*
* *Assume u is accessible from S.*
* *Let Psu be some lightest path from s to u.*
* *Let (x,y) be an edge in Psu, x in S, y in U.*
* *Psx is Reisha of lightest path*
* *w(Psx) = delta(s,x).*
* *for x in S, the induction assumption holds*
* *d(x) = delta(s,x)*
* *w(Pyu)=\>0*
* because lights are non-negative
* by **claim 1** on (x,y):
* d(y)\<=d(x)+w(x,y)
* The algoirthm choose u in this step thus:
* d(y)\>=d(u)
* In total:
*_delta(s,u)_ = w(Psu) = **w(Psx) + w(x,y) + w(Pyu)***
* w(Psx) + w(x,y) + w(Pyu) = **delta(s,x)+w(x,y)+w(Pyu)***
* delta(s,x)+w(x,y)+w(Pyu) = **d(x) + w(x,y) + w(Pyu)***
* d(x) + w(x,y) + w(Pyu) \>= d(x)+w(x,y)\>= d(y) **\>=** _d(u)_*
30
What is the *bottle neck* problem?
*_Definition:_*
* For source vertex s and vertex u:
* *bottle neck* in path P is:
* w(minimal edge in P)
* B(s,u):
* *B(s,s) = **infinity***
* Largest *bottle neck* within all paths from s to u
* If no such path exists - **minus infinity**
*_The problem:_*
* *Input: weighted graph G=(V,E,w) and source vertex s*
* *_Find B(S,u) for every u in V._*
31
* bottle neck problem:*
* *explain BRelax(u,v,w)*
*BRelxa(u,v,w):*
* There's an edge between u and v
* b[v] - ***current largest bottle neck from s to u.***
* *Check if there's a path s to u with a larger bottle neck:*
* if b[v]
* b[v] = min{b[u],w(u,v)}
32
* BottleNeck(G, w, s)*
* Explain the initialization step.*
33
* BottleNeck(G, w, s)*
* Explain the loop step.*
34
*BottleNack*
* *What is the main statement?*
* *what is claim 1?*
* *what is claim 2?*
* *what is the observation?*
35
In the proof of the *correntness statement* there are three cases we need to check.
_What are they?_
* We need to prove that for any vertex u, the moment it enters S, b[u]=B(s,u) is satisfied.*
* Note: by the observation this equality hold until the end of the run.*
*_Cases to check:_*
* *u=s*
* *No path from s to u*
* *There's a path from s to u, and u is not s.*
36
* BottleNeck corretness statement proof*
* How is the first case proved?*
*_s = u._*
* *We set b[s] = infinity at the initialization step.*
* *s is the first to enter S*
* *B(s,s) = infinity by definition.*
37
BottleNeck corretness statement proof
How is the second case proved?
*_There is no path from s to u_*
* *B(s,u) = minus infinity*
* *The 2nd claim tells us that b[u]\<=B(s,u), always.*
* *b[u] = minus infinity*
38
BottleNeck corretness statement proof
* Third case:*
* *it is proved using induction. induction on what?*
*_On the order of removal of vertices from Q_*
## Footnote
*AKA, u = EXTRACT-MAX(Q)*
39
BottleNeck corretness statement proof
* third case:*
* *what is the induction proof?*
40
*BottleNeck,* what is the proof for **claim 1?**
41
*BottleNeck, 2nd claim proof.*
*_Recall: 2nd claim_*
*All along the algorithm, for each vertex v, b[v]\<=B(s,v) is satisfied.*
42
* What is the algorithm for the attached problem?*
* What is its run-time?*
43
* What is the main statement?*
* what are the two claims we use?*
44
*How is the 1st claim proved?*
45
*How is the 2nd claim proved?*
_*Induction on the length of the path **i***_
46
*How is the main statement proved?*
47
Which algorithm is designed to find the lightests paths when negative weights are allowed?
*_Bellman-Ford_*
48
*_Describe Bellman-Ford's algorithm_*
49
*Analyze Bellman-Ford run-time*
50
* Bellman-Ford*
* Assume all vertices are accessible from s*
* We can run first BFS to identify the unaccessible vertices and avoid them.*
* *_Theorem:_*
* There exists a lightest path from s to v, for all v in V, **if and only if** there is no path from s to v which contains a circle of negative weight.*
*_Prove the theorem_*
51
* Bellman-Ford*
* What are the two claims which help us prove the correctness of BF?*
52
* Bellman-Ford*
* The 1st claim is proved using a theorem and an observation**. What are they?*
53
* Bellman-Ford*
* How the theorem of the 1st claim is proved?*
54
* Bellman-Ford,*
* How the 1st claim is solved*
55
* Bellman-Ford*
* How is the 2nd claim proved?*
56
*What is the algoirthm for the attached problem?*
57
* Find-Negative-Cycles.*
* What are the claims we use for the proof?*
58
* Find-Neg-Circle*
* What is the proof for the 2nd claim?*
59
* Find-Neg-Circle*
* What are the lemmas we use for the 1st claim?*
60
* Find-Neg-Circle: _1st claim_*
* What is the proof for the 2nd lemma?*
61
* Find-Neg-Circle:*
* what is the proof for claim 1, based on the two lemmas?*
62
*How is this problem solved?*
* solution:*
* we'll use reduction to "shortest path between two vertices" problem.*
63
* TrafficLightProblem*
* Explain the input translation phase*
64
* TrafficLightProblem*
* we run Dijkstra after the input translation step. Then, what is the output translation function?*
65
*TrafficLightProblem*
* *what is the main theorem?*
* *what is the helping theorem?*
66
* TrafficLightProblem*
* what is the proof for the helping theorem?*
67
* TrafficLightProblem*
* what is the proof for the main theorem?*
68
* TrafficLightProblem*
* what is the run-time of this algorithm?*
69
*What are some basic assumptions we proved, before jumping into Dijkstra and BF?*
A path from s to u which passes by a negative weight circle can never produce a "shortest path", thus noted as **negative infinity.**
A shortest path enforces all its subpaths to be also shortest paths.
A shortest path is definitley a simple path.
70
* Relaxation is the only means by which shortest path estimates and predecessors change.*
* The algorithm differ in how many times they relax each edge and the order in which they relax edges.*
* What is the difference between Dijkstra and BF regarding the number of edges they relax?*
* Dijkstra relax each edge at most once*
* BF relax each edge |V|-1 times.*
71
* Shortest paths:*
* List all main properties.*
* *Triganlge inequality*
* *Upper-bound inequlity*
* *No-path property*
* *Convergence property*
* *Path relaxation property*
* *Predecessor-subgraph property.*
72
***Assuming there are no negative cycles**, prove BF sets v.d = delta(s,v) for every v in V*
