Weel 4 Flashcards
(15 cards)
Why is the assumption that consumers perfectly observe price and other characteristics generally wrong?

What is a simple example of consumer search in a homogeneous market?

How is the reservation price determined? What is the reservation price?
EB(R) - c = 0
A consumer searches for a better price until the expected benefit is below the expected costs. Thus the reserve price any price for which you would accept any value below.
What is the effect of a higher cost to find the new price?
It means the reserve price is increased as well.
What is the notation of the strategy of the firm?
F(p)
What is the result of the Diamond paradox?

What is the proof for which price equilibria in a price search game cannot be a mixed strategy?

What are critical assumptions of the Diamond paradox?

What happens to the seach cost model when we introduce a second type of consumer?
We set that there are N = 2 firms. They set prices and produce the good at constant returns to scale. Normalize marginal cost to 0.
Firms and consumers play a simultaneous moves Bertrand game: an individual firm chooses a price taking the prices of the rival firms, and consumer search behavior, as given.
Consumers choose an optimal search strategy taking the price distribution as given.
Denote a firm’s strategy as F(p). This representation allows for mixed strategies.

What is the definition of a market equilibrium?

What is the formula of the expected benefit in a model which allows a mixed strategy?
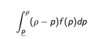
What is the formula to solve to get the reservation price? (When allowing for a mixed strategy)
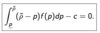
What are the results of firm pricing in the price search game?
Result: Given consumer search behavior, no firm will charge a price above ρtilde so the upper bound of the price distribution must bep = min {ρ ̃, v } . By implication, consumers will not search beyond the first firm.
- Intuition: Suppose p > ρ ̃ and consider a firm charging p. This firm will have no customers because, after visiting, they will all leave and search again and no consumer will return because 1 − F (p) = 0.
- The firm would gain by deviating to charging ρ ̃.
We shall focus on the case ρ ̃

What is the expected profit when other firms charge according to F(p)? How can it be used to solve for 𝜌̃?

How to the variables in the search price game model affect each other?



