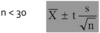Week 4 - Confidence Intervals Flashcards
Most common CIs?
90%, 95% or 99%
(0% to 100% are possible, though not usually desirable)
Hypothesis testing involves generating an ____________ about the ___________ ____________.
hypothesis, population parameter
Confidence Interval (CI) estimate…
Range or interval of values for parameters with a level of confidence attached (95% confidence that the interval contains the parameter)
Why are confidence ‘intervals’ also called ‘confidence interval estimates’?
Because the method used to calculate confidence intervals is an estimation.
Why Confidence Interval Estimate vs. Point Estimate?
Generally, point estimates are not accurate enough to provide information about the parameter, or the variability within the parameter.
Estimation uses sample data to generate ________ in the population.
Parameters
Do the properties of CLT hold if the population is normally distributed and the population is > 30?
Yes
95% confidence interval means that
We are 95 % confident that interval contains mew
When Student’s t Distribution?
- Distribution not normal
- n < 30
What type of sample is used in confidence interval calculations?
Random sample is preferred.
Measurements of sample population are called _________.
Parameters.
What is Statistical Inference?
Process of reaching a conclusion about a population based on information from a sample of that population
What is mu1 - mu2?
Difference in means
In CI >= 30 formula, what are:
X bar,
Z,
s, and
n?
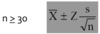
X bar = Point Estimate
Z = value from Z table
s = standard deviation
n = sample size
What is Sp?
Pooled Estimate of Common Standard Deviation
What is mud?
Mean difference
How do you calculate confidence interval?
CI = point estimate +- margin of error
Point Estimate = X bar
Margin of Error = (Z*(s/(square root of ‘n’)))
therefore,
CI = X bar +- (Z*(s/(square root of ‘n’)))
*Z or t value, based on sample size*
When do you use the CI estimation for mud?
- When you have a continuous outcome, and
- When you have two matched/paired samples,
- Unit of analysis is a pair
When do you use the CI estimation for mu?
- When you have a continuous outcome, and
- When you have a single sample, and
- When you want to estimate for the population mean for that sample.
Do the properties of CLT hold true if sample is < 30 and normally distributed?
Yes.
What is formula for CI for mud?
Xbard = Σ(x1 - x2)/n
In confidence interval estimates, _____________ gives the range of values above and below the ___________.
margin of error
point estimate
Can you use t distribution for large n?
Yes, because when n is large, t is approximately equal to standard normal distribution (Z).
The words ______ and ______ clues that we’re calculating Mean Difference.
before, after
pre, post
To get a smaller interval, do what?
Either lower level of confidence or increase n.
Measurements of sample data are called ____________.
Statistics
Types of Stastical Inference
- Estimation
- Hypothesis Testing
Confidence Interval (formula)
CI = Point Estimate ± Margin of Error
Disadvantages of using t-distribution to calculate confidence intervals:
- Wider intervals
- Must be able to assume that the underlying distribution is normal.
Why Student’s t Distribution?
- n < 30
- Cannot use z distribution b/c CLT does not hold
- Sample point estimates may not be reliable estimate of true population values
Is the point estimate representative of the entire population?
No. It is based on one sample and does not consider the variability within the parameter.
Explain mean difference.
Mean difference computes the mean (average) of differences between pre and post values. Measurements are dependent.
Mean difference = Σ(Xa - Xb)/n
Ex. BMI study…pre BMI (X1a), post BMI (X1b),
sum of differences divided by n
Mu, which represents the mean of the population is a __________.
Parameter or Stastic
Parameter
Estimation determines
likely values for an unknown population parameter.
What is best single estimator for parameter (e.g., mean)?
Point estimate
In CI < 30 formula, what are:
X bar,
t,
s,
n?
X bar = Point Estimate
t = value from t table
s = standard deviation
n = sample size
True or False: There will always be some degree of uncertainty when you caculate point estimates based on your sample.
True
Sample statistics are analyzed to…
support or reject the hypothesis about the parameter.
Which is better? Confidence Interval or Point Estimate.
Why?
Confidence Interval Estimates
Generally, point estimates are not accurate enough to provide information about the parameter, or the variability within the parameter.
Do the properties of CLT hold if the population is not normally distributed and < 30?
No.
What can be said about the sample drawn from the population in both
estimation and hypothesis testing?
The sample is random
When estimating difference in means, what is formula for Point Estimate?
mu1 - mu2
Explain difference of means.
Mean of all pre measurements - Mean of all post measurements
Measurements are independent.
Ex. Pre BMI (X1a), Post BMI (X1b)
(Xbara - Xbarb)
Key Points (3) of Student’s t Distribution?
- It is a set of distributions, not a single distribution. Collectively, these sets assume the shape of a bell shaped curve.
- Uses the parameter, degrees of freedom (df)
df = n-1
- If n is sufficiently large, student’s distribution (t) is approximately equal to standard distribution (z)
X bar, represents the sample mean of a __________.
Parameter or Stastic
Statistic
Do the properties of CLT hold true if the population < 30 and normally distributed?
Yes.
