Week 4

Question 1

What is heteroskedasticity?

Answer 1

The variance does not remain constant over the regression. Can be denoted as:

Question 2

Derive that the OLS estimator is still unbiased in the case of hetroskedacity.

Answer 2

Question 3

Derive the variance-covariance matrix of the OLS estimator in case of hetroskedacity.

Answer 3

Question 4

Derive that the OLS estimator is still consistant in case of heteroskedasticity.

Answer 4

Question 5

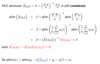
How are the White heteroskedasticity-robust standard errors computed?

Answer 5

Question 6

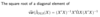
How is the variance-matrix estimated if we make the additional assumption of normality u|X ~ N(0, Ω)

Answer 6

Question 7

If we assume normality what is the impact on the distribution of β^hat

Answer 7

Question 8

Why is the OLS model no longer BLUE in case of heteroskedasticity?

Answer 8

The 5’th assumption does not hold.

Question 9

How can we test for heteroskedasticity?

Answer 9

We can use the Breusch-Pagan test.

Question 10

What are the steps for the Breusch-Pagan test?

Answer 10

Question 11

What are the variables you choose in a Breusch-Pagan test when you are using the White test (with and without crossterms).

Answer 11

Question 12

What is the WLS estimator?

Answer 12

If you have a DGP where you know how the variance changes based on the x_i (now denoted as h(x_i)), then you can transform the data such that this variance remains stable.

You then get y_i* = y_i / sqrt(h(x_i)), x_i0* = 1 / sqrt(h(x_i)), x_i1* = x_i1 / sqrt(h(x_i)), …, u_i* = u_i / sqrt(h(x_i)). Then you have that the Var(u_i*) = Var(u_i) / h(x_i) = σ² (thus homoskedasticity).

Question 13

Show that the WLS estimator is the OLS estimator in a linear regression model (for transformed
data) that satisfies the Gauss-Markov assumptions.

Answer 13

Question 14

Answer 14

Question 15

In case of heteroskedasticity, in what sense is the WLS better than the OLS?

Answer 15

Question 16

What are the steps of FWLS?

Answer 16

Question 17

When is the FWSL used?

Answer 17

When we can not find appropriate specification Var(u_i|x_i) ~ σ²h_i with known h_i.

Question 18

What are the steps used for the Iterated FWLS?

Answer 18

Question 19

In what sense is the FWLS estimator better than the OLS estimator in case of (correctly specified) heteroskedasticity?

Answer 19

Question 20

What are the properties of the FWLS estimator?

Answer 20

• asymptotically FWLS estimator has properties of WLS estimator

Question 21

For a large sample size n: What can we conclude from a large difference in the White heteroskedasticity-robust standard errors between the OLS and (F)WLS estimators? What can we conclude from a large difference between the OLS and (F)WLS estimators?

Answer 21

Huge differences between OLS and (F)WLS estimators suggest non-linear relationship.