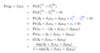Week 2 Flashcards
(16 cards)
What is a ordered probit/logit model?
A model where you group into multiple categories. Note that this is the probit model, the logit model has CDF G(.).

What is the diference between the ordered probit and logit model?
The only difference is that we use the standard logistic CDF instead of the standard normal CDF.
What is the standard logistic CDF?
G(z) = exp(z) / (1 + exp(z))
Derive the probabilities for a ordered logit/probit model with (m =) 3 possible outcomes (yi = 0, yi = 1, yi = 2).
This is for the probit model, the logit model is the same but has G(.) instead of Φ(.)

Derive the likelyhood and loglikelyhood function of the MLE of the ordered logit/probit model.

Why does (image) hold?

Since:

Show that the ordered logit/probit models with (m =) 2 outcomes is the binary probit/logit model.

Why should you not include a constant β0 in a ordered logit/probit model?
If you add β0 and τ1, τ2, … you get the same DGP, and thus you estimate the same thing twice.
What are the estimates of the probabilities of y1, y2, y3 (in the ordered logit/probit model)?
Note: the beta’s should include a hat.

What is the Percentage correctly predicted for the ordered logit/probit model?

What is the Multinomial logit model?

In a Multinomial model with (m =) 3 possible outcomes, what are these probabilities?

Interpret the coefficients in terms of the logarithm of the odds ratio P(yi = 1 | xi) / P(yi = 0 | xi) and the logarithm of the odds ratio P(yi = 2|xi) / P(yi = 0|xi) from the Multinomial logit model.
We can create a odd’s ratio between the yi = 0 and yi = 1 (see image). If we take the ln of the function then we can get the same function (without the exp). Then we can see that β1(1) > 0 there is a positive effect of xi1 on the probability of yi = 1 relative to yi = 0.

Why do we have:

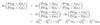
What is a different interpretation of a binary logit model using Ui(.)?

Show that the alternative of the binary model Ui(.) is equivalent.