Unit 6 - Vibration Control

Question 1

Possible effects of mechanical vibrations in structures are:-

Answer 1

1. Damage to the structure. This only results from gross vibrations such as result from earthquakes.
2. Disturbance of the occupants. The degree of movement may be sight but can create unease especially when the person is lying down. Moreover windows and fitments may rattle which adds to unease and fears about safety.
3. Vibrations of partitions creating sound within rooms. Rooms that require particularly low noise levels may need special treatment.
4. Vibrations may upset sensitive operations such as the manufacturing of micro components as found in computer chips, or optical lens manufacture.

Question 2

What does vibration control measures aim for

Answer 2

Vibration control aims to limit the transmission of vibration between one component and another.

Vibration control methods involve decoupling a driven vibration component from another linked component.

Question 3

Internal sources of vibration

Answer 3

• Industrial machinery: These may be out of balance rotary machines or impact machines (metal bashing, wood machining).
• Building services plant: Air handling units and power generators
• Movement of human beings: Footsteps particularly.

Question 4

External sources of vibration

Answer 4

Nearby industrial installations

Road traffic, particularly HGVs on poorly maintained roads

Surface railway traffic

Underground railways

Building operations such as pile driving

Blasting for mineral extraction or civil engineering projects

Question 5

As part of the task of vibration control we may need to;

Answer 5

Measure vibration magnitudes in a building

Predict vibration magnitudes in a planned building

Assess vibration magnitudes in terms of their effects on human beings

Specify measures to reduce vibration magnitudes

Question 6

Free vibration

Answer 6

Free vibration, where the system is at first displaced from the equilibrium position and then set free. For a perfectly elastic system with no energy loss (damping) the resulting oscillations would continue indefinitely

Question 7

Forced vibration,

Answer 7

Forced vibration, where the vibrating system is coupled to an external vibration that determines the frequency and amplitude of the vibration

Question 8

Vibration in six possible motions

Answer 8

Vibration can be analysed into six possible motions, the

• three orthogonal axis and three rotations about those axis.
• These are referred to as six degrees of freedom.

Dealing with anything other than one degree of freedom is complex

• Usually one of the six modes is dominant so can focus on that

Question 9

Simple one degree of freedom system with vibration along one axis

Answer 9

Question 10

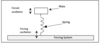
what are we interested in in a a simple isolating system

Answer 10

In a simple isolating system we are interested in the effect of the driving system upon the mass-spring system.

Question 11

what will the motion of the mass and force vary with

Answer 11

The motion of the mass and the force transmitted to the mass will vary with the frequency of the driving system.

Force transmissibility, tf , is the ratio of the force applied to the mass-spring system at the driving point to the force transmitted by the isolating system.

Displacement transmissibility, td , is the ratio of the displacement of the driving point to the displacement transmitted.

Question 12

displacement transmissibility

Answer 12

If the vibration of the machine is such that its rms displacement is xd metres, and the resulting vibration of the support has an rms displacement of xt metres, the displacement transmissibility will be t, where

Question 13

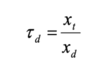
what is force transmisbilyu

Answer 13

The force transmissibility is the ratio of the force exerted by the isolating system to the farce applied to it;

Question 14

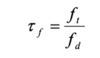
simple system transmissibility equation

Answer 14

For simple systems (single mass and vibration only in one direction, i.e. single degree of freedom, and without damping like in Figure 6.1), the two transmissibility’s have the same value.

Transmissibility varies with frequency according to the equation

Question 15

variation of transmissibility with the ratio of frequency to the natural or resonant frequency

Answer 15

The variation of transmissibility with the ratio of frequency to the natural or resonant frequency is shown in Figure 6.2.

• At frequencies far below the resonant frequency [A], transmissibility is close to 1 and the input and output are similar.
• As the frequency rises [B], the transmissibility rises and eventually reaches a peak at the natural or resonant frequency of the system (*f0*) [C**].
• As the frequency increases further, the transmissibility decreases to the neutral value of 1 when the frequency ratio reaches 1.41 (√2) [D].
• At this point the input and output are equal. For driving frequencies greater than this crossover point, transmissibility progressively decreases and the output vibrations will be less than the input vibrations [E]. Thus the mass will be isolated from the driving vibrations.

Question 16

Damped vibrations around resonance and therefore reduces transmissible

Answer 16

At first this may appear that damping may be disadvantageous but in practice damping has benefits;

• The resonance peak at f**0 can cause problems during the run-up of machines such as washing machines as the speed increase and passes through the resonance peak.
  
  • Without damping the gross vibration of the machine could be a problem.
• An undamped isolator would be very sensitive to changes in the driving frequency.
  
  • Damping would help settle down quickly after any change.
• Damping increases the range of frequencies covered by the isolator.
  
  • This eases the task of designing the isolator when the driving frequency may be not known precisely

Question 17

how to achieve the best possible isolation.

Answer 17

The frequency of driving vibrations is normally out of our control

By making f**0 as low as possible we can achieve maximum isolation of driving frequency

Low natural frequencies are achieved by large masses suspended on floppy springs.

The natural frequency of the mass spring system can be lowered by increasing the total mass.

• eg a machine mounted on a heavy structural base (an inertia base).

Question 18

Other considerations for isolation

Answer 18

• The springs will need to be at least stiff enough to support the machine’s weight.
• An inertia base will lower the centre of gravity and so increase the stability of the system
• An inertia base allow a more even weight distribution and adds rigidity to the system.
• An inertial base can act as an acoustic shield to the vulnerable floor area beneath the machine

Question 19

Isolating performance hall

Answer 19

1. The structure is divided into two or more layers with vibration isolation between each layer
2. The basement layer needs to have high acoustic impedance usually achieved through the use of heavy reinforced concrete foundations and basement substructures.
3. Levels above the isolation plane also need to have high acoustic impedance and to be stiff.
4. Resilient mounts for isolation designed with their natural resonant frequency below the lowest frequencies of significance as determined by site surveys.

Question 20

Floating Floors purpose

Answer 20

For a room that needs isolation from vibration of its supporting floor, a floating floor can be used.

At its simplest, a floating floor is a floor layer that is not nailed or glued to the subfloor and has a resilient layer sandwiched between the two layers.

Common materials are glass fibre matting, cork, polymeric sheeting and foams.

• For more demanding vibration control the structural floor is mounted on vibration isolators.

The isolators are designed to take account of the weight distribution across the room when the room is fully fitted with its equipment.

Question 21

Floating floor example

Answer 21

A radio broadcasting suite has two rooms:

• one the control room and one the broadcasting room.
• Both rooms would be sited upon floating floors but the control room would be heavier due to its greater amount of equipment

The installation needs to avoid any flanking vibration entering the isolated floor layer via the room walls

• leave a gap around the perimeter of a simple floating floor.

Question 22

Human response to vibration in buildings

Answer 22

Whole body vibration can be a problem to the operators and other occupants of various machines and forms of transport.

Vibration in buildings can arise from a number of sources both inside and outside and is similar to annoyance caused by environmental noise.

• levels experienced are typically low, but the context is one where they can be disturbing to the normal processes of life
  
  • such as sleeping and working at tasks requiring concentration

results of vibration exposure include tiredness, stress and increased likelihood of accidents and mistakes in work.

Question 23

BS 6472 Guide to evaluation of human exposure to vibration in buildings. Part 1:2008; Vibration sources other than blasting

Answer 23

In BS 6742, the vibration dose value (VDV) is the quantity used to assess human response to building vibration exposure.

Separate assessments are made of daytime vibration (07.00 and 23.00) and night- time vibration (23.00 to 0700).

Question 24

continuous Vibration

BS 6472-1

Answer 24

uninterrupted during one of the assesment period periods.

Question 25

Intermittent vibration

BS 6472-1

Answer 25

occurs in one or more shorter bursts, which may start suddenly or build up over a period.

Question 26

Occasional vibration

BS6472-1

Answer 26

less frequent and less predictable than intermittent vibration.

Question 27

Impulsive vibration

BS6472-1

Answer 27

builds up rapidly to a peak, and may be designated as continuous, intermittent or occasional.

Question 28

VDV

BS62472-1

Answer 28

It is recommended that the quantity measured is the vibration dose value or VDV. This is calculated using the 4th root of 4th power integration (see equation (6.6)) and can be measured directly by many modern instruments.

VDV is measured in units of ms-1.75 and can be given one or more subscripts to clarify the frequency weighting used (b or d) and the assessment period (T) involved.

For example, VDVb,night refers to a VDV assessment using b weighting (and therefore is a measure of vertical vibration) over the night-time period from 23.00 to 07.00.

An assessment is based on the highest of the weighted VDVs assessed on each of the three axes.

Question 29

eVDV

Answer 29

the estimated vibration dose value, eVDV, may be calculated from rms vibration measurements If equipment with that cant derive VDV is available

Question 30

Vibration damage to buildings

Answer 30

Parts 1 and 2 of BS 7385 consider the possibility that buildings may be damaged by vibration exposure.

Damage to buildings can vary from cracks in plaster to serious structural damage.

even when significant vibration is present cracking can have a number of causes, especially in new buildings.

Question 31

Measuring building vibration

Answer 31

The best measurement position may be very obvious or require a number of stages, each of which will introduce additional uncertainties.

The measured vibration magnitude depends on whether the vibration of the ground itself is measured, or whether measurements are made on the lowest floor of a building, or on a higher floor.

Question 32

measurements representative of the vibration of the ground itself;

Answer 32

measurements of the vibration of a large masonry structure embedded in the ground will be representative of the vibration of the ground itself;

suitable structures would include a solid floor slab in contact with the ground and forming part of an existing or former building.

If no such structure exists then measurements can be made

large pieces of masonry embedded in the ground for the purpose, or on a metal stake hammered into the ground.

Question 33

floor to floor attenaton vibration

Answer 33

Likely to be a loss of amplitude when vibration is transferred into a building structure other than a solid floor slab.

This floor-to-floor attenuation will result in a loss of amplitude as vibration energy is transferred across the junction between different building elements.

Offset by the greater tendency of higher floors to vibrate;

vibration magnitudes are normally greater on upper than on lower floors in a multi-storey building.