Unit 16 Alternating Current

Question 1

What is the E (inst)

Answer 1

The voltage at any any point on the waveform

Question 2

What is E (max)

Answer 2

The maximum ,or peak voltage

Question 3

What is sin <0

Answer 3

the sin of the angle of rotation

Question 4

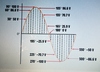
The peak value, or amplitude, is measured from

Answer 4

zero to the highest value obtained in either the positive or negative direction. The peak value is one-half of the peak-to-peakp.463

Question 5

Probably the single greatest advantage of AC is

Answer 5

the fact that AC can be trans-formed and DC cannot. A transformer permits voltage to be stepped up or down. Voltage can be stepped up for the purpose of transmission and then

Question 6

Thomas Edison,

Answer 6

an American inventor, proposed powering the country with low-voltage DC. He reasoned that low-voltage DC was safer for people to use than higher-voltage AC. $1 per lamp to light the fair with low-voltage DC.

Question 7

Nikola Tesla,argued that DC was impractical for large-scale applications. The

Answer 7

however, argued that DC was impractical for large-scale applications. PS: The 1904 World’s Fair not only introduced the first ice cream cone and the first iced tea but was also the first World’s Fair to be lighted with “electric candles.” Westinghouse Company, headed by George Westinghouse, 25 cents per lamp to light the fair using higher-voltage AC.

Question 8

AC differs from DC in that

Answer 8

AC reverses its direction of flow at periodic in-tervals positive again. The voltage remains negative for some length of time and then changes back to positive again. Each time the voltage reverses polar-ity, the current flow through the circuit changes direction.

Question 9

AC Square Wave

Answer 9

One waveform frequently encountered is the square wave

Question 10

Can DC voltage have a square wave

Answer 10

Yes

Each time the switch position is changed, current flows through the resistor in a different direction. Although this circuit will produce a square wave AC, it is not practical.

Pg 457

Question 11

Can DC produced a square wave?

Answer 11

Yes

Square wave AC can be produced with a switch and two batteries.

Although this circuit will produce a square wave AC, it is not practical.

Question 12

Square waves are generally produced by electronic devices called

Answer 12

oscillators.

Question 13

Another common AC waveform is the

Answer 13

triangle wave The triangle wave is a linear wave, one in which the voltage rises at a constant rate with respect to time. Linear waves form straight lines when plotted on a graph.

positive value of 100 volts after 2 milliseconds. The voltage will be 25 volts after 0.5 milliseconds, 50 volts after 1 milliseconds, and 75 volts after 1.5 milliseconds.

Question 14

The most common of all AC waveform

How meny degress

Answer 14

sine waves

The sine wave contains a total of 360 electric degrees.

It reaches its peak positive voltage at 90 degress , returns to a value of 0 volts at 180 Degrees, increases to its maximum negative voltage at 270 Degress , and returns to 0 volts at 360 Degrees . Each complete waveform of 360 Degress is called a cycle.

Question 15

complete cycles that occur in one second is called

is measured

Answer 15

frequency.

hertz (Hz).

Question 16

Sine waves are so named because

Answer 16

the voltage at any point along the waveform is equal to the maximum, or peak, value times the sine of the angle of rotation.

Question 17

NOTES

Because the loop is cutting the flux lines at an angle, it must travel a greater distance between flux lines during the first degrees of rotation. Consequently, fewer flux lines are cut per second, which results in a lower induced voltage.

Answer 17

Recall that 1 volt is induced second, which results in a lower induced voltage. Recall that 1 volt is induced in a conductor when it cuts lines of magnetic flux at a rate of 1 weber per second (Wb/s). One weber is equal to 100,000,000 lines of flux.

Question 18

The following formula can be used to determine the instantaneous value at any point along the sine wave:

Answer 18

E (_INST) = E _(MAX) X sin < 0

E (_INST) = the voltage at any point on the waveform

E (_MAX) = the maximum, or peak, voltage

sin < 0 = the sine of the angle of rotation

Question 19

A sine wave has a maximum voltage of 138 V. What is the voltage after 78 Degrees of rotation?

Answer 19

Solution:

E _(INST) = E _(MAX) sin < 0

** E _(INST) = 138 X 0.978 (sin of 78Degrees )**

** E _(INST) = 134.964 V **

The formula can be changed to find the maximum value if the instantaneous value and the angle of rotation are known or to find the angle if the maximum and instantaneous values are known:

** E _(MAX) = E _(INST) / sin<0**

** sin <0 = E _(INST) / E _(MAX)**

Question 20

A sine wave has an instantaneous voltage of 246 V after 53Degrees of rotation. What is the maximum value the waveform will reach?

Answer 20

Solution:

** E _(MAX) = E _(INST) / sin < 0**

** E _(MAX) = 246V / 0.799Degrees**

** E _(MAX) = 307.885 V**

Question 21

A sine wave has a maximum voltage of 350 V. At what angle of rotation will the voltage reach 53 V?

Answer 21

Solution:

** sin < 0 = E _(INST) / E _(MAX) **

sin < 0 = 53 V / 350 V

sin < 0 = 0.151

Note:

0.151 is the sine of the angle, not the angle. < 0 = 8.685 Degrees

Question 22

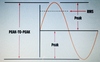
What are Peak-to-Peak and Peak Values

Answer 22

The peak-to-peak value is measured from the maximum value in the positive direction to the maximum value in the negative direction. The peak-to-peak value is often the simplest measurement to make when using an oscilloscope.

NOTE:

The peak value, or amplitude, is measured from zero to the highest value obtained in either the positive or negative direction. The peak value is one-half of the peak-to-peak value.

Question 23

What is RMS Values

Answer 23

**RMS, or effective, value. **

It is the value indicated by almost all AC voltmeters and ammeters. RMS stands for root-mean-square, which is an abbreviation for the square root of the mean of the square of the instantaneous currents.

The RMS value can be found by dividing the peak value by the square root of 2 (1.414) or by multiplying the peak value by 0.707 (the reciprocal of 1.414). The formulas for determining the RMS and peak values are

RMS = peak X 0.707

peak = RMS X 1.414

Question 24

A sine wave has a peak value of 354 V. What is the RMS value?

Answer 24

Solution:

RMS = peak X 0.707

RMS = 354 V X 0.707

RMS =250.278

Question 25

An AC voltage has a value of 120 V RMS. What is the peak value of voltage?

Answer 25

Solution:

** peak = RMS X 1.414**

** peak = 120 V X 111.414**

** peak = 169.68 V**

When the RMS values of voltage and current are used, the result is the same amount of power as like values of DC voltage and current. If 100 V RMS is applied to a 100- V resistor, the resistor will produce 100 W of heat. AC voltmeters and ammeters indicate the RMS value, not the peak value. Oscilloscopes, how-ever, display the peak-to-peak value of voltage. All values of AC voltage and current used from on in thix textare RMS value unless otherwise stated.

Question 26

What are Average Values voltage and current?

Answer 26

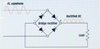
Average values of voltage and current are actually DC values. The average value must be found when a sine wave AC voltage is changed into DC with a recti-fier

(Figure 16–12) . The rectifier shown is a bridge-type rectifier that produces full-wave rectification. This means that both the positive and negative half of the AC waveform are changed into DC. The average value is the amount of voltage that would be inndicated by a DC voltmeater if it were connected across a loads resistor.

Question 27

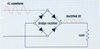
Notice in Figure 16–13 that the voltage waveform turns on and off, but it never changes polarity. The current, therefore, never re- verses direction.

What is it called?

Answer 27

This is called pulsating DC. The pulses are often referred to as ripple.

Question 28

What are Average Values of voltage

Answer 28

actually DC value

The average value must be found when a sine wave AC voltage is changed into DC with a recti-fier (Figure 16–12)

Question 29

FIGURE 16–12 The bridge rectifier changes AC voltage into DC voltage.

Answer 29

The rectifier shown is a bridge-type rectifier that produces full-wave rectification. This means that both the positive and negative half of the AC waveform are changed into DC. The average value is the amount of voltage

Question 30

what is a ripple wave

Answer 30

that would be indicated by a DC voltmeter if it were connected across the load resistor. The average voltage is proportional to the peak, or maximum, value of the waveform and to the length of time it is on as compared with the length of time it is off (Figure 16–13) . Notice in Figure 16–13 that the voltage waveform turns on and off, but it never changes polarity. The current, therefore, never re- verses direction. This is called pulsating DC. The pulses are often referred to as ripple. The average value of voltage will produce the same amount of power as a nonpulsating source of voltage such as a battery (Figure 16–14) . For a full- wave rectified sine wave, the average value of voltage is found by multiplying the peak value by 0.637 or by multiplying the RMS value by 0.9.

Question 31

For a full- wave rectified sine wave, the average value of voltage is found by

Answer 31

multiplying the peak value by 0.637 or by multiplying the RMS value by 0.9.

Question 32

To determine the average voltage for a half-wave rectifier, multiply

Answer 32

multiply the peak value by 0.637 or the RMS value by 0.9 and then divide the product by 2. Because only half of the AC waveform has been converted into DC, the average voltage will be only half that of a full-wave rectifier

Question 33

A half-wave rectifier is connected to 277 VAC. What is the average DC voltage?

Answer 33

Solution

average = RMS X 0.9 / 2

average = 277 V X 0.9 /2

average = 124.65 V

Question 34

Power in an AC Circuit

Answer 34

True power, or watts, can be produced only when both current and voltage are either positive or negative. When like signs are multiplied, the product is positive ( 1 3 1 5 1 , or 2 3 2 5 1 ), and when unlike signs are multiplied the product is negative ( 1 3 2 5 2 ). Because the current and volt-age are both either positive or negative at the same time, the product, watts, is always positive (Figure 16–20) .

Question 35

Notes:

Resistive Loads

Answer 35

In DC circuits, there is only one basic type of load, which is resisresistive. Even motor loads appear to be resistive because there is a conversion of electri-cal energy into mechanical energy. In this type of load, the true power, or watts, is the product of the volts times the amperes. In AC circuits, the type of load can vary depending on several factors. AC loads are generally described as being resistive, inductive, or capacitive, depending on the phase-angle relationship of voltage and current and the amount of true power produced by the circuit. Inductive and capacitive loads are discussed in later units. Re-sistive loads are loads that contain pure resistance, such as electric heating tive. equipment and incandescent lighting. Resistive loads are characterizedby the facts that 1. they produce heat. 2. the current and voltage are in phase with each other. Any time that a circuit contains resistance, electrical energy is changed into heat. When an AC voltage is applied to a resistor, the current flow through the resis-tor is a copy of the voltage (Figure 16–19) . The current rises and falls at the same rate as the voltage and reverses the direction of flow when the voltage reverses polarity. In this condition, the current is said to be in phase with the voltage.

Question 36

Skin Effect in AC Circuits

Answer 36

When current flows through a conductor connected to a source of DC, the electrons flow through the entire conductor (Figure 16–21) . The conductor offers some amount of ohmic resistance to the flow of electrons, depending