Understanding and communicating risk Flashcards
If there are 4 questions in a multiple-choice test what are the odds that you will guess incorrectly?
=3 to 1
Think as Chance of success=1
Chance of failure=3
This is a related topic which you will need to understand and (in particular) the relationship with probability. Later in this online material, we will look at the interchangeability between Relative Risk (RR) which is based on probability and Odds Ratio (OR) which (yes, you’ve guessed it!) is based on odds.
In the real world, you may have come across the concept of odds in gambling. Odds are ratios of a player’s chances of losing to his or her chances of winning, or the average frequency of a loss to the average frequency of a win.
Let’s go back to the example for probability we used in Q1. If a player owns 1 of 4 tickets, the probability of winning is 1 in 4 and the odds of winning are 3 to 1.
You may be wondering why we are talking about gambling in an MBBS research course. Further, you may be asking yourself why – if the probability is such an easy concept to use - do we have an alternate way to express the chance of an event occurring?
The short answer is that odds can be helpful when we want to compare how much larger one probability is relative to another. Let’s go back to our gambling example – imagine we bought three tickets the probability of winning would be 3 in 4, or ¾ or 75%. The odds would be 75 to 25. We can simplify this to 3 to 1. This means that the winning event is three times more likely to occur than losing.
One last point. Remember – the bookies always win in the end!
Relative Risk is the ratio of the probability of an outcome in an exposed group compared to the probability of an outcome in an unexposed group - true or false?
True - this is the definition and also how you calculate relative risk.
For example, RR is used to compare the risk of an adverse outcome when receiving a medical treatment versus no treatment (or placebo), or when exposed to an environmental risk factor versus not exposed.
The odds ratio is the ratio of the probability of exposure in people with an outcome compared to the probability of exposure in people without an outcome - true or false?
False - The odds ratio is the ratio of the odds of exposure in people with an outcome compared to the odds of exposure in people without an outcome.
Remembering that OR is very similar to RR, however, OR is calculated by using the ratio of odds whereas RR is calculated by using probabilities (usually expressed as percentages) Check back to question 1 and 3 on probability and RR if you need a reminder.
Relative risk is a ratio of probabilities, but which probability is the numerator:
A - the probability of the event (or outcome) occurring in an exposed group
B - the probability of the event occurring in an unexposed group
The answer is A.
Relative Risk is the ratio of the probability of an outcome in an exposed group divided by the probability of an outcome in an unexposed group.
Odds Ratio is a ratio of odds, but which is the denominator:
A - odds of the outcome in people exposed
B - odds of the outcome in people unexposed
The answer is B.
As you may have guessed the odds ratio is a ratio of the odds. Just remember that we calculate the ratio as the odds of developing the outcome if you’ve been exposed (i.e. smoking and cancer) divided by the odds of developing the outcome if you haven’t been exposed (i.e. smoking without cancer).
Odds Ratio= (Smokers with cancer / Smokers without cancer) /(Non-smokers with cancer / Non-smokers without cancer)
You have calculated that the RR of cancer associated with smoking is 3. How can you communicate that to a patient?
A - That as a smoker they are 3 times more likely to develop cancer.
B - That smokers are 300% more likely to be diagnosed with cancer.
C - That they shouldn’t smoke
D - All of the above
The answer is D, you could say all of the above.
An RR of 3 reveals that the risk of cancer is 3 times higher in smokers compared to controls, which can be expressed as a percentage i.e. 300%. Which means that is it very risky to smoke.
Remember is that the RR value can be easily interpreted depending on whether the value number falls above or below 1. Assuming the causal effect between the exposure and the outcome, values of RR can be interpreted as follows:
RR = 1 means that exposure is not associated with the outcome.
RR < 1 means that the risk of the outcome is decreased by the exposure.
RR > 1 means that the risk of the outcome is increased by the exposure.
The odds ratio of stress fracture occurring with a bone metabolic treatment is OR = 1. What should you tell your patient?
You can tell your patients that exposure to the treatment does not affect the odds of the side effect occurring.
Remember is that the OR value can be easily interpreted depending on whether the value number falls above or below 1 (just like with RR).
OR=1 Exposure does not affect the odds of the outcome
OR>1 Exposure associated with higher odds of the outcome
OR<1 Exposure associated with lower odds of the outcome
True or false - it does not matter whether we use the OR or the RR to calculate, represent and communicate risk.
The answer is False.
OR is only a good estimate of the RR when an event is rare. To see why we must look at the denominators in the equations for OR and RR.
When an event is common the odds ratio overestimates the risk because the denominator for the odds is much lower than the denominator for the probability.
But when an event is rare the odds ratio is a good estimate of the relative risk because the denominator for odds and probability is almost identical.

A drug rep tells you that their new medicine reduces asthma exacerbations compared to standard treatment and the OR is 0.5. The rep even has a peer-reviewed publication in The Lancet to back up the assertion. Would you give your patients the treatment?
You might want to ask what the RR is because the OR overestimates to benefits if the event (i.e. cure) is common.
RR (i.e. risk ratios) and OR (odds ratios) are often used interchangeably. The term should not be used interchangeably because they are calculated and interpreted quite differently. It is important to keep the concepts separate and to be precise in the language you use.
And remember - before thinking of OR and RR alone you need to think whether the outcome is common or rare!
When do I use RR and OR?
Essentially RR and OR cannot be swapped interchangeably. For rare events the OR can be used as an estimate of the RR, but not for common events. We will come back to this later (so don’t worry if it does not make sense now) but RR is more useful for explaining how successful a treatment is at preventing events like fracture or stroke, whist OR is useful for a capturing the rare side effect.
e. g. Use RR to compare the risk in two different groups of people (e.g. smokers and non-smoker), usually used in prospective cohort studies.
e. g. Use OR to measure of association between an exposure and an outcome (e.g. smoking and cancer), usually used in case-control studies (where the incidence is less than 10%).
Calculating RR
RR is calculated using the contingency table by dividing the probability of an event occurring for one group (A) divided by the probability of an event occurring for a second group (B).
RR can be calculated using the following method using A 2x2 table. In this example, a study has followed up 200 patients, 100 smokers (i.e. exposed) and 100 non-smokers (i.e. unexposed). At the end of the study, they found that 30 of the smokers and 10 of the non-smokers developed lung cancer.
Draw RR contingency table and perform ratio calculation

Calculating OR
OR can also be calculated using the contingency table by dividing the odds of an event occurring for one group (A) divided by the odds of an event occurring for a second group (B). The formula used to calculate OR is different for RR.
Draw OR contingency table and perform ratio calculation


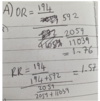
B.
A multicentre, retrospective, case-control study reported the following data linking cigarette smoking and myocardial infarction (MI). 1940 cases were reported to have suffered an MI compared to 9909 patients who had not. 432 of the MI patients were smokers, whereas 672 of control patients were smokers.
Construct a 2x2 table with this data and calculate the odds ratio and relative risk of having an MI for smokers (show your working).

C.
Construct a 2x2 table with the data in the spreadsheet (download from Insendi) and calculate the odds ratio and relative risk of a depression diagnosis in low income individuals (show your working).


In your clinic, you have a patient who is a regular marijuana smoker, a regular cigarette smoker and from a low-income household. We would like to communicate the risk to your patient.



