Types of Data - Descriptive Statistics

Question 1

Qualitative data

Answer 1

Information in non-numerical form e.g. written words describing an event or opinion. This type of data is more difficult to interpret and score but gives detailed insight into behaviour.

Question 2

Quantitative data

Answer 2

Information in numerical form e.g. score on a psychology test out of 20. This type of data is relatively easy to interpret and score and you can make clear comparisons between participants/conditions. The majority of quantitative data is generated by experiments, questionnaires and observations. Analysis of the numerical data requires the researcher to calculate measures of central tendency and dispersion and often conduct statistical tests.

Question 3

Strengths of quantitative

Answer 3

• Data can be analysed using inferential statistics which mean I can be analysed and compared easily. - Data collection tends to be highly reliable as it often uses objective measures (definite).

Question 4

Weaknesses of quantitative

Answer 4

• Method of measurement may limit participants’ responses which will lack detail, therefore making the data less valid. -This in turn makes it less useful as we cannot suggest why something has happened.

Question 5

Strengths of Qualitative data

Answer 5

• In depth data, and high detail as participants can express themselves exactly as they want to. - It is less likely that key or rare observations will be ‘lost’ through the process of simplifying the data – more valid

Question 6

Weaknesses of qualitative data

Answer 6

• Subjective measures means that data collection may be invalid as recording or interpretation of responses may be biased by the researcher’s opinions or feelings. -Data are individual so it may be difficult to make generalisations from the findings and compare between the groups.

Question 7

Primary and secondary data

Answer 7

There are many ways to conduct research and there are many different ways to classify the different types of research. One way is to distinguish between the collection of primary and secondary data. -Primary data - is data that is collected by a psychologist straight from the source e.g. through their own experiments, correlations, observations, case studies or self-reports. -Secondary data - is where a psychologist will use data from previous studies by other researchers. The purpose may be to re-analyse, combine or compare results. They are re-using data in a new analysis.

Question 8

Three steps in recording & presenting data.

Answer 8

1. Data is initially recorded in RAW DATA table
2. This raw data is then SUMMARISED into a SUMMARY TABLE using totals, % & the appropriate central tendencies.
3. Summarised data can then be placed into an appropriately labelled GRAPH

Question 9

Level of measurement

Answer 9

1. Nominal (simplest) 2. Ordinal (more precise) 3. Interval & Ratio (most precise)

Question 10

Data can be treated as nominal

Answer 10

• Results are in totals in two or more named categories. • This shows the number of times something occurred. • Likely to be collected from closed questions in self-reports or from structured observations For example- (a) The number of people who helped or didn’t help (b) The number of smokers or non smokers (c) The number of males or females

Question 11

Data can be treated as ordinal

Answer 11

• Results are in able to be placed in rank order (e.g. in positions such as 1st,2nd and 3rd etc or highest and lowest) • The difference between each rating, rank or score is not known For example coming 1st,2nd 3rd in a beauty contest. • Or does not have to be equal For example putting class test scores in rank order does not have to be equal, 1st place could be 90/100, 2nd 88/100 but 3rd 80/100

Question 12

Data can be treated as interval/ratio

Answer 12

•Results are made up of number that come from a scale of equal or known units • INTERVAL data can go into negative values EG temperature • RATIO data has an absolute zero and so are often mathematical units For example; weight, distance or time

Question 13

IMPORTANT TO REMEMBER!

Answer 13

• We can treat interval/ratio as it is or treat it as ordinal or nominal (i.e. convert it) - Ordinal can be treated as it is but can also be treated (converted) as nominal. - Nominal cannot be made more precise & so can only be treated in this way.

Question 14

Analysing quantitative data The mean

Answer 14

-Is the score commonly known as the average & the most suitable to use for data treated as interval or ratio but can also be used for data treated as ordinal. It is calculated by adding up all the scores & then dividing this by the total number of scores. :) uses all raw data :(is affected by extreme scores so may be misleading

Question 15

The Mode

Answer 15

Is the value or score that occurs most frequently. If there are two models it is Bi-modal, if more than 2 it is multi modal. This is most suitable for data treated as nominal. Not influenced by extreme scores & can show most popular value.  Does not use all the data & so may not be representative.

Question 16

The median

Answer 16

is the middle value when the data is placed in order and so half the scores lie above the median & half below. If there are even numbers there will be two middle value & so those are added together & divided by 2. This is most suitable for data treated as ordinal & can also be used for data treated as interval/ratio. :) Not affected by extreme scores :(But can be distorted by small samples (e.g. 2, 3, 4, 98, 112, median = 5)

Question 17

Measure of dispersion

Answer 17

A measure of dispersion gives an indication of how spread out the results within a data set are. In other words, these tell us about the spread of data and so can tell us how much variation there was between participants scores (the more variation the more chance that individual differences affected the data). -The range -The variance

Question 18

The range

Answer 18

Is calculated by finding the difference between the highest & lowest score +1 in a data set (plus 1 is there to allow for measurement error). This is suitable for data treated as interval/ratio & ordinal. :) Easy to calculate :( Can be influenced by extreme scores & so it may be misleading as it tells us nothing about the distribution of the other scores.

Question 19

Variance

Answer 19

just as the mean can tell us more than the mode, a measure called the variance can tell us more than the range. Rather than looking at the extremes of the data set, the variance considers the difference between each data point and the mean, this is called deviation. These deviations are then squared and then added together and the total is divided by the number of scores in the data set minus 1. :) They take every score into account and are therefore not affected by outliers.

Question 20

How to calculate standard deviation

Answer 20

SD tells us about the spread of data around the mean. It helps us to understand whether data is closely clustered around the mean or very spread out.

Question 21

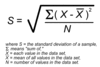
Steps to calculate a standard deviation for the data

Answer 21

1. Add up the number of scores to give you n
2. Calculate the mean (add test scores together and divide by n)
3. Calculate the difference between the individual score and the mean score
4. Square the difference
5. Sum the square scores
6. Divided by n (variation)
   
   1. To calculate the SD =square of variance

Question 22

Strengths and weaknesses of standard deviation

Answer 22

:) More precise measurement because all the values of the data are taken into account

:( Affected by extreme scores at either end of the data set.

Question 23

Summarising data with the use of graphs

Answer 23

Graohs are used to illustrate findings. Thye may illustrate frequencies, percentages or any of the measures of central tendency. Different graphs are used for different types of data. You need to know which to choose and how to sketch them.

Question 24

The key to presenting data graphically is to keep it simple. To do this follow these rules:

Answer 24

• We only need one graph to summarise the data
• The graph should be clearly labelled
• There should be no raw data included

Question 25

Bar charts

Answer 25

This is used when the data are in seperate categories, that iis, data that is measured on a nominal scale. Thebars on the chart must be separate.

Question 26

Stacked bar charts

Answer 26

when bars relating to the same category put on top of each other

Question 27

Paired bar charts

Answer 27

are similar to stacked bar charts but they are more useful if two or more levels of the independent variable are to be compared.

Question 28

Pie Chart

Answer 28

A circular graph divided into sectors. Each portion of the circle represents a numerical proportion of a whole. The data must consist of frequencies or proportions that can be expressed as a fraction. These figures must then be converted to angles (proportions of 360 degrees)

Question 29

Histogram

Answer 29

These are used to show the pattern in a whole data set where there is continuous data, that is, data that is measured on an ordinal or interval scale. They are used to illustrate the distribution of a set of scores.

Question 30

Line graphs

Answer 30

These are an alternative way to represent the data shown in a histogram. Instead of drawing columns a point is marked at the height of the frequency of each score, these points are then joined to form a line. These are sometimes known as frequency polyogns.

Question 31

Scatter diagrams

Answer 31

These are used to display the findings of correlational studies. Each point on the grsph represents both scores for one participant.