Correlations Flashcards
What is a correlation?
carrying out a piece of research using a correlation involves measuring two variables. Correlations look for a relationship between two variables. This is not to say that one thing causes another, simply that one thing varies in accordance with another. They allow us to statistically analyse naturally occurring events that could not be set up experimentally. A correlation refers to a measure of how strongly two or more variables are related to each other. This means that a correlation is not a method of collecting data but a way of analysing data already collected.
Correlations are shown on scatter graphs by plotting dots to represent each pair of scores.
-A positive correlation is a relationship between variables where as one increases, the other increases OR as one decreases the other decreases. E.g. temperature and amount of ice cream bought (the hotter it is, the more ice creams are bought) -A negative correlation is a relationship between variables where as one variable increases the other decreases. E.g. temperature and number of hot water bottles bought (the hotter it is, the less hot water bottles are bought). Note that like a positive correlation, a negative correlation still indicates that some kind of relationship exists.
**REMEMBER ASSOCIATION DO NOT MEAN CAUSATION!**
-For example; there is almost certainly a very high positive correlation between the length of a person’s right arm and the length of their left arm. But the length of a person’s left arm did not determine the length of their right arm. They are both determined by oher factors i.e. genetics, diet etc. Similarly, my goldfish lives in a tank on my desk. The more fizzy drinks I consume, the more active my fish is. It’s tempting to assume there is CAUSAL relationship - seeing the bubbles in my glass makes her excited. In reality, there is no causal relationship; both variables are affected by a third factor - temperature. The hotter the weather, the more I drink and fish are more active in warmer water.
Obtaining data for correlational analysis
In order to look for a correlation between two variables, it must be possible to measure them numerically i.e. the data must be quantitative. This means that the participants’ score cannot just be in named categories. Although the scales for each variable may be different, they both need to be numerical (or it must be possible to convert them to numbers).
Scatter diagrams
You will only be able to sketch a scatter diagrams if you have two scores/numbers/sets of data for each individual participant - therefore it cannot be nominal data as you need individual scores! For example: height in cm (variable 1) and their weight in kg (variable 2) Intelligence measured as score on IQ test (variable 1) and their monthly income in £s (variable 2) Therefore each participant needs an individual score, so you can plot them as an individual ‘‘x’’ on the graph
What are the range of techniques that can be used in correlational analyses to collect appropriate data, for example:
- Self-reports, such as interviews and questionnaires through rating scales.
- Observations… for example, the number of aggressive acts observed in the playground correlated with number of swear words used during conversation.
- Many scientific measurements used in psychological investigations, such as reaction time, pulse rate and galvanic skin response (a measure of stress)
Correlation coefficients
A correlation co-efficient tells us about the strength of the relationship between two variables.
A correlation coefficient refers to a number between -1 and +1 and states how strong a correlation is between two variables and the direction of the correlation (+ive, -ve or no correlation)
If the number is close to +1 then there is a positive correlation. If the number is close to -1 then there is a negative correlation. If the number is close to 0 then the variables are uncorrelated
Scale of correlation
-1__________________0__________________+1 Correlations are very good for showing possible relationships between variables and sometimes are the only practical or ethical way of carrying out an investigation. You will need to be able to estimate the strength of the correlation from some diagrams, the diagrams below show some representations.
Writing a correlational hypotheses
1-Correlational hypothesis
2-Null hypothesis
1- A correlational hypothesis would predict that there will be a relationship or correlation between the two variables. e.g. there will be a significant positive correlation between the amount of sleep and levels of concentration. The more sleep in hours, the higher the level of concentration measure in minutes.
2- A null hypothesis states that no relationship/correlation will be found. e,g, there will be no significant relationship between the amount of sleep an individual has, measure in hours and their level of concentration measured in minutes. Any relationship found will be due to chance.
Strength of correlations
- We can identify relationships between variables without having to manipulate behaviour. So it can be used in situations where experimentation would otherwise be impossible or unethical.
- Correlations are often used to suggest ideas for future experimental research in order to determine cause and effect relationships (e.g. may create a hypothesis for future experiments).
Weaknesses of correlations
- Cause and effect CANNOT be established, correlations can only show a relationship between variables, so we would need further research to establish cause and effect
- Other unknown variable(s) may have caused the link between the co-variables being measured. Therefore correlations may lack validity.
Statistical testing
Spearman’s Rho Test In order to calculate the correlation coefficient and thus assess the strength of the relationship between two variables it is necessary to carry out a statistical test. The test you need to know related to correlations is the spearman’s rho test. Remember if it comes out as a negative value this is showing you the direction of the correlation.
n= number of participants
n2= number of participants squared
d = difference
d2 = difference squared
Σ =sum of
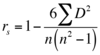
LOOK at booklet for the whole spearmans calculations
LOOK at booklet for the whole spearmans calculations


