Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

Calculus (Khan) > Trig Identities > Flashcards

Trig Identities Flashcards

1
Q

What are
identities
used for?

A

Rewriting

  • *expressions** in
  • *equivalent**, but
  • *more useful**, forms.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Reciprocal and quotient identities:

sec (Θ) = ___

A

Reciprocal and quotient identities:

sec (Θ) = 1
cos (Θ)

Cosine and secant always multiply exactly to 1.
(They are reciprocal functions.)

In the right triangle definitions, cosine is adjacent over hypotenuse, and secant is hypotenuse over adjacent. In the unit circle, the adjacent side is the radius with length 1, so it simplifies to just the hypotenuse.​

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Reciprocal and quotient identities:

csc (Θ) = ___

A

Reciprocal and quotient identities:

csc (Θ) = 1
sin (Θ)

Sine and cosecant always multiply exactly to 1.
(They are reciprocal functions.)

In the right triangle definitions, sine is opposite over hypotenuse, and cosecant is hypotenuse over opposite. In the unit circle, the opposite side is the radius with length 1, so it simplifies to just the hypotenuse.​

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Reciprocal and quotient identities:

tan (Θ) = ___

A

Reciprocal and quotient identities:

tan (Θ) = sin (Θ)
cos (Θ)

Right triangle definition:
opposite
adjacent

Unit circle definition:
sin (Θ)
cos (Θ)

Same Θ in multiple right triangles, so
tan (Θ) must be the same.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Reciprocal and quotient identities:

  • *cot (Θ) = ___**
  • (two things)*
A

Reciprocal and quotient identities:

cot (Θ) = 1 = cos (Θ)
tan (Θ) sin (Θ)

Tangent and cotangent always multiply exactly to 1.
(They are reciprocal functions.)

Cotangent is defined as adjacent over opposite. In the unit circle, the opposite side is the radius with length 1, so it simplifies to just the adjacent.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

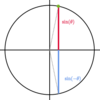
Symmetry and periodicity identities:

sin (−Θ) = ___

A

sin (−Θ) = −sin (Θ)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Symmetry and periodicity identities:

cos (−Θ) = ___

A

cos (−Θ) = cos (Θ)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

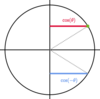
Symmetry and periodicity identities:

tan (−Θ) = ___

A

tan (−Θ) = −​tan (Θ)

Proof:

  • tan (Θ) = sin (Θ)
    cos (Θ)
    (unit circle definition)
  • tan (−Θ) = sin (−Θ)
    cos (−Θ)
    (substitution)
  • tan (−Θ) = − sin (−Θ)
    cos (Θ)
    (symmetry identities)
  • tan (−Θ) = −tan (Θ)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

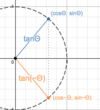
Symmetry and periodicity identities:

sin (Θ + ___) = sin (Θ)

A

2π

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Symmetry and periodicity identities:

cos (Θ + ___) = cos (Θ)

A

2π

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Symmetry and periodicity identities:

tan (Θ + ___) = tan (Θ)

A

π

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Cofunction identities:

cos (90° − Θ) = ___

A

sin (Θ)

All the cofunction identities look the same.

Going from Θ to 90°−Θ is
equivalent to
reflecting the angle over the line
y = x.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Cofunction identities:

In radians,
how would you write
cos (Θ) in terms of its
cofunction?

A

cos (Θ) =
sin (π/2 − Θ)

All the cofunction identities look the same.

Going from Θ to π/2 − Θ is
equivalent to
reflecting the angle over the line
y = x.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Cofunction identities:

sec (90° − Θ) = ___

A

csc(Θ)

All the cofunction identities look the same.

Going from Θ to 90°−Θ is
equivalent to
reflecting the angle over the line
y = x.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Cofunction identities:

In radians,
how would you write
sec (Θ) in terms of its
cofunction?

A

sec (Θ) =
csc (π/2 − Θ)

All the cofunction identities look the same.

Going from Θ to π/2 − Θ is
equivalent to
reflecting the angle over the line
y = x.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Cofunction identities:

tan (90° − Θ) = ___

A

cot (Θ)

All the cofunction identities look the same.

Going from Θ to 90°−Θ is
equivalent to
reflecting the angle over the line
y = x.

17
Q

Cofunction identities:

In radians,
how would you write
tan (Θ) in terms of its
cofunction?

A

tan (Θ) =
cot (π/2 − Θ)

All the cofunction identities look the same.

Going from Θ to π/2 − Θ is
equivalent to
reflecting the angle over the line
y = x.

18
Q

Pythagorean identities:

What is the
Pythagorean identity?

A

sin2 (Θ) + cos2 (Θ) = 12,
which simplifies to

sin2 (Θ) + cos2 (Θ) = 1

It comes from applying the Pythagorean theorem to the right triangle below.

19
Q

Pythagorean identities:

Arrange the following into a Pythagorean identity:
tan2 (Θ), sec2 (Θ), 1.

A

tan2 (Θ) + 1 = sec2 (Θ)

It comes from applying the Pythagorean theorem to the right triangle below.

20
Q

Pythagorean identities:

Arrange the following into a Pythagorean identity:
1, csc2 (Θ), cot2 (Θ).

A

cot2 (Θ) + 1 = csc2 (Θ)

It comes from applying the Pythagorean theorem to the right triangle below.

21
Q

Angle sum and difference identities:

sin (A + B) = ___

A

sin (A + B) =
sin (A) cos (B) + cos (A) sin (B)

Directly from the diagram below.

22
Q

Angle sum and difference identities:

sin (A − B) = ___

A

sin (A − B) =
sin (A) cos (B) − cos (A) sin (B)

Can be proved from the sum formula.

Proof:

  • sin (A + B) = sin (A) cos (B) + cos (A) sin (B)
    (sum formula)
  • cos (−B) = cos (B)
    (symmetry identity)
  • sin (−B) = −sin (B)
    (odd function identity)
  • sin (A + (−B)) = sin (A) cos (−B) + cos (A) sin (−B)
    (substitution)
  • sin (A − B) = sin (A) cos (B) − cos (A) sin (B)
    [sign change] [no sign change] [sign change]
23
Q

Angle sum and difference identities:

cos (A + B) = ___

A

cos (A + B) =
cos (A) cos (B) − sin (A) sin (B)

Directly from the diagram below.

24
Q

Angle sum and difference identities:

cos (A − B) = ___

A

cos (A − B) =
cos (A) cos (B) + sin (A) sin (B)

Can be proved from the sum formula.

Proof:

  • cos (A + B) = cos (A) cos (B) −​ sin (A) sin (B)
    (sum formula)
  • cos (−B) = cos (B)
    (symmetry identity)
  • sin (−B) = −sin (B)
    (odd function identity)
  • cos (A + (−B)) = cos (A) cos (−B) − sin (A) sin (−B)
    (substitution)
  • cos (A − B) = cos (A) cos (B) + sin (A) sin (B)
    [sign change] [no sign change] [sign change]
25
Q

Angle sum and difference identities:

tan (A + B) = ___

A

tan (A + B) =
tan (A) + tan (B)
1 − tan (A) • tan (B)

Proof:

  • tan (A) = sin (A)
    cos (A)
    (definition of tangent)
  • tan (A + B) = sin (A + B)
    cos (A + B)
    (substitution)
  • = sin (A) cos (B) + cos (A) sin (B)
    cos (A) cos (B) − sin (A) sin (B)
    (sine and cosine addition formulae)
  • = sin (A) cos (B) + cos (A) sin (B) (÷ cos (A) cos (B))
    cos (A) cos (B) − sin (A) sin (B) (÷ cos (A) cos (B))
    (dividing numerator and denominator by same value)
  • ( sin (A) / cos (A)) + sin (B) / cos (B))
    1 − (sin (A) sin (B)) / (cos (A) cos (B))
    (expanding division to each term)
  • = tan (A) + tan (B)
    1 − tan (A) • tan (B)
    (simplifying with definition of tangent)
26
Q

Angle sum and difference identities:

tan (A − B) = ___

A

tan (A − B) =
tan (A) − tan (B)
1 + tan (A) • tan (B)

Same as the tangent angle addition formula with the signs reversed.

Proof:

  • tan (A + B) = tan (A) + tan (B)
    1 − tan (A) • tan (B)
    (tangent angle addition formula)
  • tan (−B) = −tan (B)
    (tangent symmetry identity)
  • tan (A + (−B)) = tan (A) + tan (−B)
    1 − tan (A) • tan (−B)
    (substitution)
  • = tan (A) − tan (B)
    1 + tan (A) • tan (B)
27
Q

Double angle identities:

sin (2A) = ___

A

sin (2A) =
2 sin (A) cos (A)

Proof:

  • sin (A + B) = sin (A) cos (B) + cos (A) sin (B)
  • (sine angle addition formula)*
  • 2A = A + A
  • sin (A + A) = sin (A) cos (A) + cos (A) sin (A)
  • (substitution)*
  • = 2 sin (A) cos (A)
28
Q

Double angle identities:

cos (2A) = ___

A

cos (2A) =
2 cos2 (A) − 1

Proof:

  • cos (A + B) = cos (A) cos (B) − sin (A) sin (B)
    (cosine angle addition formula)
  • 2A = A + A
  • cos (A + A) = cos (A) cos (A) − sin (A) sin (A)
    (substitution)
  • cos (2A) = cos2 (A) − sin2 (A)
  • sin2 (A) + cos2 (A) = 1
    sin2 (A) = 1 − cos2 (A)
    (Pythagorean identity)
  • cos (2A) = cos2 (A) − (1 − cos2 (A))
    (substitution)
  • = cos2 (A) − 1 + cos2 (A)
    (distribute negative sign)
  • = 2cos2 (A) − 1
29
Q

Double angle identities:

tan (2A) = ___

A

tan (2A) =
2 tan (A)
1 − tan2 (A)

Proof:

  • tan (A + B) = tan (A) + tan (B)
    1 − tan (A) • tan (B)
    (tangent angle addition formula)
  • 2A = A + A
  • tan (A + A) = tan (A) + tan (A)
    1 − tan (A) • tan (A)
    (substitution)
  • = 2 tan (A)
    1 − tan2 (A)

Calculus (Khan) (4 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions