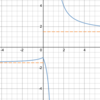
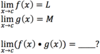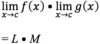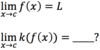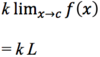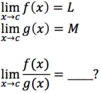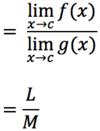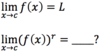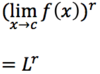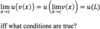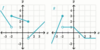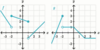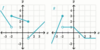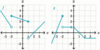Limits & Continuity Flashcards
(87 cards)
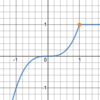
# _define_: limit
The
value that a
function approaches as the
input approaches
some value.
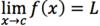
How would you
- *read** this
- *aloud**?
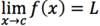
The
- *limit** as
- x* approaches c of
- *f(x)**
- *equals L.**
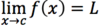
In plainspeak,
what do
limits do?
Describe how
- *functions behave**
- *near a point.**
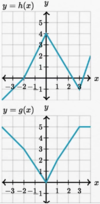
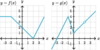
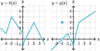
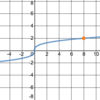
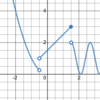
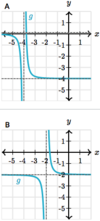
What is a
- *reasonable estimate** for the
- *limit of g(x)** as:
x→3?
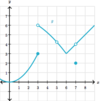
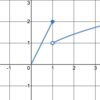
As x→3, the limit of g(x)
does not exist
(g(x) is defined; but there is
no limit because there is
no finite value that g(x) approaches)
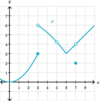
What is a
- *reasonable estimate** for the
- *limit of g(x)** as:
x→5?
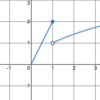
As x→5, the limit of g(x)
approaches approximately 4.2
(g(x) is undefined; and there is a
limit because there is a
finite value that g(x) approaches)
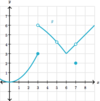
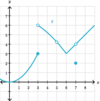
What is a
- *reasonable estimate** for the
- *limit of g(x)** as:
x→7?
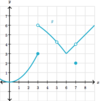
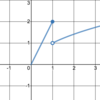
As x→7, the limit of g(x)
approaches 4
(g(x) is defined; and there is a
limit because there is a
finite value that g(x) approaches)
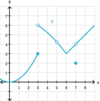
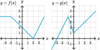
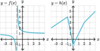
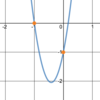
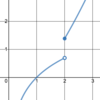
Is this
possible?
- *g(x) is defined** at (x, g(x)); the
- *limit exists** at that point; and the
- *limit equals g(x)** at that point?
Yes.
See the limit of g(x) below as x→8.
The function value and the limit can be the same, although the
function value is irrelevant to finding the limit.
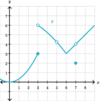
Is this
possible?
- *g(x) is defined** at (x, g(x)); the
- *limit exists** at that point; and the
- *limit does not equal g(x)** at that point?
Yes.
See the limit of g(x) below as x→7.
The function value and the limit can be different because the
function value is irrelevant to finding the limit.
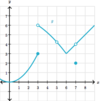
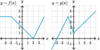
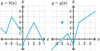
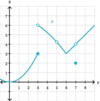
Is this
possible?
g(x) is defined at (x, g(x))
and the
limit does not exist at that point?
Yes.
- See the limit of g(x) below as x→3.*
- Just because the function is defined does not mean that the limit exists.*
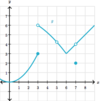
Is this
possible?
g(x) is undefined at an x value
and the
limit exists at that x value?
Yes.
- See the limit of g(x) below as x→5.*
- Just because the function is undefined does not mean that the limit does not exist.*
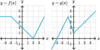
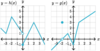
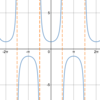
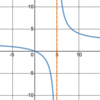
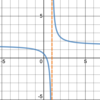
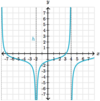
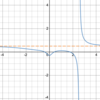
What a
- *reasonable estimation** of the
- *limit** of the function below as
- *x→2**?
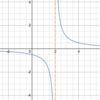
The
limit does not exist.
We don’t say “unbounded” because the function is not approaching a finite value and it does not go in the same direction as x→2**.

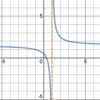
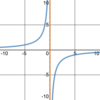
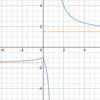
What a
- *reasonable estimation** of the
- *limit** of the function below as
- *x→2**?
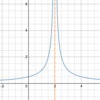
The
limit is unbounded.
The limit does not exist, but we say “unbounded” because the function is not approaching a finite value, although the two sides are going in the same direction.
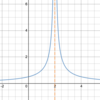
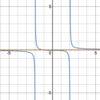
What
kind of limit
is this?

A
one-sided limit.
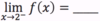
How would you
- *read** this
- *aloud**?
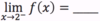
The
limit of f(x) as x approaches 2
from the left.

How would you
- *read** this
- *aloud**?

The
limit of f(x) as x approaches 2
from the right.
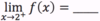
limx→2+ f(x) = _____
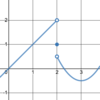
0.5

limx→2− f(x) = _____

2

For
f(x) = 4x + 2,
where can you
evaluate the limit of
f(x)?
Anywhere f(x) is defined,
which is
anywhere.
For one given function, you can take the limit at an infinite number of points. Although we only usually care about limits near interesting points.
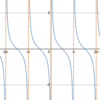
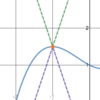
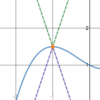
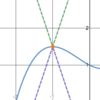
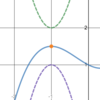
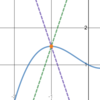
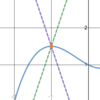
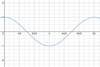
Is this
possible?
- *A sinusoid**,
- *a line**, and
- *a tangent graph** all have the
- *same limit**?
Yes.

Functions that have the same limit at a point can look very different.
Assuming this table is accurate,
is it
appropriate for
approximating
limx→2 f(x)?

No, because the
increments are too large
approaching x = 2.

Assuming this table is accurate,
is it
appropriate for
approximating
limx→2 f(x)?

- *No**, it approaches x = 2 from
- *one side only**.

Assuming this table is accurate,
is it
appropriate for
approximating
limx→2 f(x)?

- *Yes**, it approaches x = 2 from
- *both sides** at
- *smaller and smaller increments**.

If you were
constructing a table to
approximate the limit below,
what would some
appropriate values be?
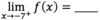
−6.9, −6.99, −6.999, −6.9999…
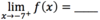
- Your values should approximate getting infinitely close to −7 from the right, which you do by approaching −7 from the right at smaller and smaller increments.*
- k+ means “approaching k from the right,” whether those values are positive or negative.*
- k − means “approaching k from the left,” whether those values are positive or negative.*
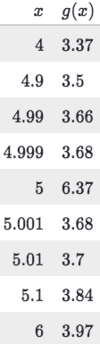
What is a
reasonable estimate for
limx→5 g(x)?

3.68
Limit value is distinct from function value.