Trees Flashcards
(20 cards)
(Easy) Merge Two Binary Trees
Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.
https://leetcode.com/problems/merge-two-binary-trees/

Approach 1: Using Recursion
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
int val=0;
if(t1==null) return t2;
if(t2==null) return t1;
t1.val += t2.val;
t1.left = mergeTrees(t1.left, t2.left);
t1.right = mergeTrees(t1.right, t2.right);
return t1;
}
Approach 2: Iterative Method
Use stack:
We start off by pushing the root nodes of both the trees onto the stack. Then, at every step, we remove a node pair from the top of the stack. For every node pair removed, we add the values corresponding to the two nodes and update the value of the corresponding node in the first tree. Then, if the left child of the first tree exists, we push the left child(pair) of both the trees onto the stack. If the left child of the first tree doesn’t exist, we append the left child(subtree) of the second tree to the current node of the first tree. We do the same for the right child pair as well.
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null)
return t2;
Stack < TreeNode[] > stack = new Stack < > ();
stack.push(new TreeNode[] {t1, t2});
while (!stack.isEmpty()) {
TreeNode[] t = stack.pop();
if (t[0] == null || t[1] == null) {
continue;
}
t[0].val += t[1].val;
if (t[0].left == null) {
t[0].left = t[1].left;
} else {
stack.push(new TreeNode[] {t[0].left, t[1].left});
}
if (t[0].right == null) {
t[0].right = t[1].right;
} else {
stack.push(new TreeNode[] {t[0].right, t[1].right});
}
}
return t1;
}
(Easy) Range Sum of BST
Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive).
The binary search tree is guaranteed to have unique values.
Example 1:
Input: root = [10,5,15,3,7,null,18], L = 7, R = 15
Output: 32
Traverse BST with DFS and if node falls in between L, R add to res.
Recursive Impl:
public int rangeSumBST(TreeNode root, int L, int R) {
int res=0;
if(root==null) return 0;
if(root.val> = L && root.val< =R) res+=root.val;
if( L < root.val) res+= rangeSumBST(root.left,L,R);
if( R > root.val) res+= rangeSumBST(root.right,L,R);
return res;
}
Iterative Impl:
public int rangeSumBST(TreeNode root, int L, int R) {
int res=0;
Stack\< TreeNode\> stack = new Stack();
stack.push(root);
while(!stack.empty()){
TreeNode top = stack.pop();
if(top.val< =R && top.val> =L) res+=top.val;
TreeNode left = top.left;
if(left!=null && L< top.val) stack.push(left);
TreeNode right = top.right;
if(right!=null && R> top.val) stack.push(right);
}
return res;
}
(Easy) Second Minimum Node In a Binary Tree
Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

public int findSecondMinimumValue(TreeNode root) {
int min = root.val;
int second\_min = Integer.MAX\_VALUE;
Stack\< TreeNode\> stack = new Stack();
stack.push(root);
int count=0;
while(!stack.empty()){
TreeNode top = stack.pop();
if(top.val\< min){
second\_min=min; min=top.val;
count++;
}
else if(top.val!= min && top.val\<=second\_min) {second\_min=top.val; count++;}
if(top.left!=null) stack.push(top.left);
if(top.right!=null) stack.push(top.right);
}
return count>=1 ? second_min: -1;
}
(Easy) Binary Tree Paths
Given a binary tree, return all root-to-leaf paths.
Note: A leaf is a node with no children.

Apply DFS and build strings and add to list.
But the catch is don’t use strings as its costly and creates new Objects for every append. Instead, use stringBuilder, and in every recursive function at the end setLength of StringBuilder to where its length was when the function was called.
Time Complexity:
List\< String\> res = new ArrayList();
public List\< String\> binaryTreePaths(TreeNode root) {
if (root == null)
return res;
binaryTreePaths(root,new StringBuilder());
return res;
}
public void binaryTreePaths(TreeNode root, StringBuilder sb){
if(root==null) return;
int len = sb.length();
sb.append(root.val);
if(root.left==null && root.right==null)
res.add(sb.toString());
else{
sb.append(“->”);
binaryTreePaths(root.left,sb);
binaryTreePaths(root.right,sb);
}
sb.setLength(len);
}
(Easy) Sum of Root To Leaf Binary Numbers
Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

int res=0;
public int sumRootToLeaf(TreeNode root) {
sumRootToLeaf(root,0);
return res;
}
public void sumRootToLeaf(TreeNode node, int sum ){
if(node==null) return;
sum = 2*sum+node.val;
if(node.left==null && node.right==null){
res+=sum;
return;
}
if(node.left!=null) sumRootToLeaf(node.left,sum);
if(node.right!=null) sumRootToLeaf(node.right,sum);
}
(Easy) Symmetric Tree
Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

Approach: Compare for equal node values and then left subtree with right subtree and right with left recursively.
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
return isMirror(root.left, root.right);
}
public boolean isMirror(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) return true;
if (t1 == null || t2 == null) return false;
return (t1.val == t2.val)
&& isMirror(t1.right, t2.left)
&& isMirror(t1.left, t2.right);
}
(Easy) All Elements in Two Binary Search Trees
Given two binary search trees root1 and root2.
Return a list containing all the integers from both trees sorted in ascending order.
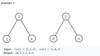
Approach: Do level order traversal on both the BST’s and merge the sorted arrays.
public List< Integer> getAllElements(TreeNode root1, TreeNode root2) {
List< Integer> tree1 = new LinkedList();
List< Integer> tree2 = new LinkedList();
List< Integer> res = new LinkedList();
dfs(root1,tree1);
dfs(root2,tree2);
int i=0,j=0;
while(i < tree1.size() || j < tree2.size()){
if(j == tree2.size() || i < tree1.size() &&
tree1.get(i) < = tree2.get(j)){
res.add(tree1.get(i));
i++;
} else if(j < tree2.size()){
res.add(tree2.get(j));
j++;
}
}
return res;
}
public void dfs(TreeNode node, List< Integer> tree){
if(node==null) return;
dfs(node.left,tree);
tree.add(node.val);
dfs(node.right,tree);
}
(Easy) Binary Tree Level Order Traversal II
Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).
Approach: Use linkedList to do addFirst operations.
public List\< List\< Integer\>\> levelOrderBottom(TreeNode root) {
LinkedList\< List\< Integer\>\> res = new LinkedList();
if(root==null) return res;
Queue\< TreeNode\> queue = new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
List< Integer> list = new ArrayList(size);
while(size> 0){
size–;
TreeNode node = queue.poll();
list.add(node.val);
if(node.left!=null) queue.add(node.left);
if(node.right!=null) queue.add(node.right);
}
res.addFirst(list);
}
return res;
}
(Easy) Cousins in Binary Tree
Two nodes of a binary tree are cousins if they have the same depth, but have different parents.
We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree.

public boolean isCousins(TreeNode root, int x, int y) {
if(root==null) return false;
Queue< List< TreeNode>> queue = new LinkedList();
if(root.left!=null)queue.add(Arrays.asList(root.left,root));
if(root.right!=null)queue.add(Arrays.asList(root.right,root));
while(!queue.isEmpty()){
int size=queue.size();
int match=0;
int parent=-1;
while(size> 0){
size–;
List< TreeNode> top = queue.poll();
if(top.get(0).val==x||top.get(0).val==y){
if(match==0){
match++; parent=top.get(1).val;
}
if(match==1){
if(top.get(1).val!=parent) match++;
}
}
if(top.get(0).left!=null)
queue.add(Arrays.asList(top.get(0).left,top.get(0)));
if(top.get(0).right!=null)
queue.add(Arrays.asList(top.get(0).right,top.get(0)));
}
if(match==2) return true;
}
return false;
}
(Medium) Smallest String Starting From Leaf
Given the root of a binary tree, each node has a value from 0 to 25 representing the letters ‘a’ to ‘z’: a value of 0 represents ‘a’, a value of 1 represents ‘b’, and so on.
Find the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

Approach:
- Do DFS and keep building string along the path
- If the right and left of a node are null, we are at a leaf node. Compare the string with res and update.
Time Complexity: 0(N) for Dfs and O(L) for string comparison where L is the length of the string. L is the max height of a tree. For a perfectly balanced tree h= (log n). So time Complexity is O(NlogN).
String res=null;
public String smallestFromLeaf(TreeNode root) {
if(root==null) return “”;
smallestFromLeaf(root,””);
return res==null ? Character.toString((char)(root.val+97)): res;
}
public void smallestFromLeaf(TreeNode root, String str){
Character ch = (char)(root.val+97);
str=ch+str;
if(root.right==null && root.left==null){
if(res == null || str.compareTo(res) < 0) res = str;
return;
}
if(root.left!=null) smallestFromLeaf(root.left,str);
if(root.right!=null) smallestFromLeaf(root.right,str);
}
(Medium) Sum Root to Leaf Numbers
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
Standard Tree paths Approach.
- Traverse all the nodes using DFS.
- Maintain the sum of the current path, if it’s a leaf node add this sum to res.
int res=0;
public int sumNumbers(TreeNode root) {
if(root==null) return 0;
sumNumbers(root, 0);
return res;
}
public void sumNumbers(TreeNode root, int sum) {
if(root==null) return;
sum = (sum*10) + root.val;
if(root.left==null && root.right==null) res+=sum;
sumNumbers(root.left,sum);
sumNumbers(root.right,sum);
}
(Medium) Maximum Difference Between Node and Ancestor
Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

Approach: check for maxDiff and update res, and return min, max in every recursion.
int res=Integer.MIN_VALUE;
public int maxAncestorDiff(TreeNode root) {
if(root==null) return 0;
maxDiff(root);
return res;
}
public int[] maxDiff(TreeNode node){
int[] left = new int[]{Integer.MAX_VALUE,Integer.MIN_VALUE};
int[] right = new int[]{Integer.MAX_VALUE,Integer.MIN_VALUE};
if(node.left!=null){
left = maxDiff(node.left);
res = Math.max(res, Math.abs(node.val-left[0]));
res = Math.max(res, Math.abs(node.val-left[1]));
}
if(node.right!=null){
right = maxDiff(node.right);
res = Math.max(res, Math.abs(node.val-right[0]));
res = Math.max(res, Math.abs(node.val-right[1]));
}
int min = Math.min(node.val,left[0]);
min = Math.min(min,right[0]);
int max = Math.max(node.val,left[1]);
max = Math.max(max,right[1]);
return new int[]{min,max};
}
(Medium) Find Bottom Left Tree Value
Given a binary tree, find the leftmost value in the last row of the tree.

public int findBottomLeftValue(TreeNode root) {
Queue\< TreeNode\> queue = new LinkedList();
queue.add(root);
int res=root.val;
while(!queue.isEmpty()){
int size=queue.size();
res=queue.peek().val;
while(size\> 0){
size--;
TreeNode top = queue.poll();
if(top.left!=null) queue.add(top.left);
if(top.right!=null) queue.add(top.right);
}
}
return res;
}(Medium) N-ary Tree Level Order Traversal

public List\< List\< Integer \>\> levelOrder(Node root) {
List\< List\< Integer\>\> res = new ArrayList();
if(root==null) return res;
Queue\< Node\> queue = new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
List< Integer> level = new ArrayList(size);
while(size> 0){
size–;
Node top = queue.poll();
level.add(top.val);
if(top.children!=null){
for(Node child: top.children) {
if(child!=null)
queue.add(child);
}
}
}
res.add(level);
}
return res;
}
(Medium) Minimum Cost Tree From Leaf Values
Each node has either 0 or 2 children;
The values of arr correspond to the values of each leaf in an in-order traversal of the tree.
The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree respectively.
Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.

Approach: Use stacks, NGE find nge. check min b/w incoming no. and stack top and add to res. This would be the min cost to remove this node from the tree.
Goal is to remove nodes from the tree with minimum cost, remove a node meaning clubbing it with an nge as a pair. And the root of this pair would be this nge as described in the question. So the smaller no. would no longer be required in the tree. And the cost of this operation would be added to ans. And the nge will be added to stack to be picked as the largest leaf value.
public int mctFromLeafValues(int[] arr) {
Stack\< Integer\> stack = new Stack();
stack.push(Integer.MAX\_VALUE); int ans=0;
for(int i=0;i\< arr.length;i++){
while(!stack.empty() && stack.peek()\< arr[i]){
int t = stack.pop();
ans+= t \* Math.min(stack.peek(),arr[i]);
}
stack.push(arr[i]);
}
while(stack.size()\> 2){
int t = stack.pop();
ans+= t \* stack.peek();
}
return ans;
}
(Medium) Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

Approach: if the left tree returns 1 || the right tree returns 1 || the current node matches, if the sum of these 3 is equal to 2, then this node will be the LCA.
TreeNode ans=null;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return ans;
if(p.val==q.val) return p;
lca(root,p,q);
return ans;
}
public boolean lca(TreeNode node, TreeNode p, TreeNode q){
int current=0;
if(node==null) return false;
if(node.val==p.val || node.val==q.val) current=1;
int left = lca(node.left,p,q) ? 1:0;
int right = lca(node.right,p,q) ? 1:0;
if(left+right+current==2) ans=node;
return (left+right+current>0);
}
(Medium) Binary Tree Zigzag Level Order Traversal
Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

Approach:
- Level Order Traversal using a queue.
- At every level change the ordering of how nodes are added to list. Use linked list so that we can add in front and at end.
public List\< List\< Integer\>\> zigzagLevelOrder(TreeNode root) {
List\< List\< Integer\>\> res = new ArrayList();
if(root==null) return res;
Queue\< TreeNode\> queue = new LinkedList();
queue.add(root);
int i=0;
while(!queue.isEmpty()){
int size=queue.size();
LinkedList< Integer> list = new LinkedList();
while(size> 0){
size–;
TreeNode node = queue.poll();
if(i%2==0) list.add(node.val);
else list.addFirst(node.val);
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
i++; res.add(list);
}
return res;
}
(Medium) Longest Univalue Path
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.
The length of path between two nodes is represented by the number of edges between them.

Approach:
We can think of any path (of nodes with the same values) as up to two arrows extending from it’s root.
Then, for each node, we want to know what is the longest possible arrow extending left, and the longest possible arrow extending right? We can solve this using recursion.
At each node calculate the result value for this node and check with max. And then return the max of the left, right arrows matching with the root.
int max=0;
public int longestUnivaluePath(TreeNode node) {
if(node==null) return max;
arrowLength(node);
return max;
}
public int arrowLength(TreeNode node) {
if (node == null) return 0;
// Recursive calls to check for subtrees
int left = arrowLength(node.left);
int right = arrowLength(node.right);
int Leftmax = 0, Rightmax = 0; // If curr node and it's left child has same value if (node.left != null && node.left.val == node.val) Leftmax=left+1;
// If curr node and it's right child has same value if (node.right != null && node.right.val == node.val) Rightmax=right+1;
max = Math.max(max, Leftmax + Rightmax);
return Math.max(Leftmax, Rightmax);
}
(Medium) Path Sum III
You are given a binary tree in which each node contains an integer value.
Find the number of paths that sum to a given value.
The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).

Approach:
- maintain HashMap of prefix path sum to check.
- and remove it at the tail of every recursive call. Tail Recursion.
int res=0; int k;
HashMap\< Integer,Integer\> prefixPathSumMap = new HashMap();
public int pathSum(TreeNode root, int sum) {
if(root==null) return res;
k=sum;
countPaths(root,0);
return res;
}
public void countPaths(TreeNode root, int sum ){
if(root==null) return;
sum+= root.val;
if(sum==k)res++;
if(prefixPathSumMap.containsKey(sum-k))
res+=prefixPathSumMap.get(sum-k);
//Add it in the hashmap for all the recursion below this current node. N1 prefixPathSumMap.put(sum, prefixPathSumMap.getOrDefault(sum,0)+1);
countPaths(root.left,sum);
countPaths(root.right,sum);
//This is the place where all the recursions of the current node N1's childrens will be done, and it will go above to the previous item in stack. That is it will go to the right child of the N1's parent now. prefixPathSumMap.put(sum, prefixPathSumMap.get(sum)-1); }
(Medium) Path Sum II
Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.
Note: A leaf is a node with no children.

Approach:
- Maintain a stack for the paths. Keep adding nodes and remove them at the tail before the function returns.
- if sum matches then create a new copy of the stack as an arrayList and add to res list.
List\< List\< Integer\>\> res = new ArrayList();
Stack<integer> path = new Stack(); int k;<br> public List< List< Integer>> pathSum(TreeNode root, int sum) {<br> if(root==null) return res;<br> k=sum;<br> validPaths(root,0);<br> return res;<br> }<br> <br> public void validPaths(TreeNode root, int sum){<br> if(root==null) return; <br> sum+= root.val;<br> path.push(root.val);<br> if(root.left==null && root.right==null){<br> if(sum==k) res.add(new ArrayList(path));<br> }<br> validPaths(root.left, sum);<br> validPaths(root.right, sum);<br> path.pop();<br> }</integer>


