Stacks Flashcards
(15 cards)
(Easy) Valid Parentheses
Given a string containing just the characters ‘(‘, ‘)’, ‘{‘, ‘}’, ‘[’ and ‘]’, determine if the input string is valid.
public boolean isValid(String s) {
Stack stck = new Stack();
for(int i=0; i\< s.length();i++){
if(s.charAt(i)=='(' || s.charAt(i)=='{' || s.charAt(i)=='[') stck.push(s.charAt(i));
if(s.charAt(i)==')'){
if(stck.empty() || stck.peek() != '(' ) return false;
stck.pop();
}
if(s.charAt(i)=='}'){
if(stck.empty() || stck.peek() != '{' ) return false;
stck.pop();
}
if(s.charAt(i)==']'){
if(stck.empty() || stck.peek() != '[' ) return false;
stck.pop();
}
}
return stck.empty() ? true : false ;
}(Easy) Min Stack
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
push(x) – Push element x onto stack.
pop() – Removes the element on top of the stack.
top() – Get the top element.
getMin() – Retrieve the minimum element in the stack.
Approach 1:
Keep differences in the stack with min.
If negative no. popped update min.
To get top element add min to it if its positive else return min.
class MinStack {
Stack stck;
long min;
/\*\* initialize your data structure here. \*/
public MinStack() { stck = new Stack\< Long \> ();}
public void push(int x) {
if(stck.empty()){
stck.push(0L);
min = x;
}
else{
stck.push(x - min);
min= Math.min(min,x);
}
}
public void pop() {
long val = stck.pop();
if(val < 0) min = min-val;
}
public int top() {
long val = stck.peek();
if(val \> 0) return (int)(val+min);
else return (int)min;
}
public int getMin() { return (int)min; }
}
Approach 2:
Using two stacks one for numbers, one for minimums.
https://leetcode.com/problems/min-stack/discuss/49016/C%2B%2B-using-two-stacks-quite-short-and-easy-to-understand
Approach 3:
https://leetcode.com/problems/min-stack/discuss/49014/Java-accepted-solution-using-one-stack
Only push the old minimum value when the current minimum value changes after pushing the new value x.
if pop operation could result in the changing of the current minimum value, pop twice and change the current minimum value to the last minimum value.
class MinStack {
public void push(int x) {
if(x < = min){
stack.push(min);
min=x;
}
stack.push(x);
}
public void pop() {
if(stack.pop() == min) min=stack.pop();
}
public int top() { return stack.peek(); }
public int getMin() { return min; }
}
(Easy) Next Greater Element I
The Next Greater Number of a number x in nums1 is the first greater number to its right in nums2. If it does not exist, output -1 for this number.
Example 1:
Input: nums1 = [4,1,2], nums2 = [1,3,4,2].
Output: [-1,3,-1]
Stacks Standard
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
if(nums2.length==0) return nums2;
if(nums1.length==0) return nums1;
HashMap< Integer, Integer> res = new HashMap();
for(int i:nums1) res.put(i,-1);
Stack< Integer> nge = new Stack< Integer>();
*nge.push(nums2[0]);
for(int x:nums2){
while(!nge.empty() && x >nge.peek()){
int val = nge.pop();
if(res.containsKey(val)) res.put(val, x);
}
nge.push(x);
}
while(!nge.empty()){
int val = nge.pop();
res.put(val, -1);
}
for(int i=0;i< nums1.length;i++) nums1[i]=res.get(nums1[i]);
return nums1;
}*
(Easy) Backspace String Compare
Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.
Note that after backspacing an empty text, the text will continue empty.
Example 1:
Input: S = “ab#c”, T = “ad#c”
Output: true
Approach 1: Build Strings
Let’s individually build the result of each string using staccks, then compare if they are equal.
Time: O(M+N)
Space: O(M+N)
Approach 2: Two Pointers
When writing a character, it may or may not be part of the final string depending on how many backspace keystrokes occur in the future.
Iterate through the string in reverse. If we see a backspace character, the next non-backspace character is skipped. If a character isn’t skipped, it is part of the final answer.
public boolean backspaceCompare(String S, String T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i \> = 0 || j \> = 0) { // While there may be chars in build(S) or build (T)
while (i \> = 0) { // Find position of next possible char in build(S)
if (S.charAt(i) == '#') {skipS++; i--;}
else if (skipS \> 0) {skipS--; i--;}
else break;
}
while (j \> = 0) { // Find position of next possible char in build(T)
if (T.charAt(j) == '#') {skipT++; j--;}
else if (skipT \> 0) {skipT--; j--;}
else break;
}
// If two actual characters are different
if (i \> = 0 && j \> = 0 && S.charAt(i) != T.charAt(j))
return false;
// If expecting to compare char vs nothing
if ((i \> = 0) != (j \> = 0))
return false;
i--; j--;
}
return true;
}
(Easy) Implement Queue using Stacks
Implement the following operations of a queue using stacks.
push(x) – Push element x to the back of queue.
pop() – Removes the element from in front of queue.
peek() – Get the front element.
empty() – Return whether the queue is empty.
Approach 1:
(Two Stacks) Push - O(1)per operation, Pop - O(n) per operation.
Use 2 stacks s1,2.
Push to S1.
Whenever a pop comes, pop from s1 add to s2. Pop the top from s2 and add back all the elements to s1.
Keep track of front in a variable during pop, and pus.
Approach 2:
(Two Stacks) Push - O(1) per operation, Pop - Amortized O(1) per operation.
https://leetcode.com/problems/implement-queue-using-stacks/solution/
Push:
public void push(int x) {
if (s1.empty())
front = x;
s1.push(x);
}
Pop:
Same as before, but add to S2 from S1 only when S2 is empty, else pop from S2.
public void pop() {
if (s2.isEmpty()) {
while (!s1.isEmpty())
s2.push(s1.pop());
}
s2.pop();
}
For top element, peek from S2 if not empty, else return front variable.
public int peek() {
if (!s2.isEmpty()) {
return s2.peek();
}
return front;
}
public boolean empty() {
return s1.isEmpty() && s2.isEmpty();
}
(Easy) Implement Stack using Queues
Implement the following operations of a stack using queues.
push(x) – Push element x onto stack.
pop() – Removes the element on top of the stack.
top() – Get the top element.
empty() – Return whether the stack is empty.
Approach 1:
Using 2 Queues:
public int pop() {
int pop=0;
while(!q1.isEmpty()) {
if(q1.size()==1){ pop=q1.poll(); break;}
front=q1.poll();
q2.add(front);
}
//We can swap q1 with q2 to avoid copying all elements from q2 to q1. while(!q2.isEmpty()) q1.add(q2.poll()); return pop; }
Using a single Queue:
When we push an element into a queue, it will be stored at back of the queue due to queue’s properties. But we need it to be in the front of the queue, not at the back. To achieve this we can invert the order of queue elements when pushing a new element.
//Whenever a new element comes add it to Queue, and remove all other elements and add them at the back of this new element. We are done.
public void push(int x) {
q1.add(x);
int sz = q1.size();
while (sz > 1) {
q1.add(q1.remove());
sz–;
}
}
(Medium) Next Greater Element II
Given a circular array (the next element of the last element is the first element of the array), print the Next Greater Number for every element.
You could search circularly to find its next greater number. If it doesn’t exist, output -1 for this num.
Example 1:
Input: [1,2,1]
Output: [2,-1,2]
public int[] nextGreaterElements(int[] nums) {
Stack< Integer> stack =new Stack< Integer>();
int[] res = new int[nums.length];
for(int i=0;i< nums.length;i++) {
while(!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
res[stack.pop()]= nums[i];
}
stack.push(i);
}
for(int i=0;i< nums.length;i++) {
while(!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
res[stack.pop()]= nums[i];
}
}
while(!stack.empty()) res[stack.pop()]= -1;
return res;
}
(Medium) Next Greater Element III
Given a positive 32-bit integer n, you need to find the smallest 32-bit integer which has exactly the same digits existing in the integer n and is greater in value than n. If no such positive 32-bit integer exists, you need to return -1.
Example 1:
Input: 12
Output: 21
https: //leetcode.com/problems/next-greater-element-iii/
1. Traverse the given number from rightmost digit, keep traversing till you find a digit which is smaller than the previously traversed digit.
2. Find the next highest digit for this element to the right side.
3. Swap with this element and add the rest to the num.
https://leetcode.com/submissions/detail/371567277/
Did this with stack and integer forming.
(Medium) Daily Temperatures
Given a list of daily temperatures T, return a list such that, for each day in the input, tells you how many days you would have to wait until a warmer temperature. If there is no future day for which this is possible, put 0 instead.
Given the list of temperatures
T = [73, 74, 75, 71, 69, 72, 76, 73],
Your output should be [1, 1, 4, 2, 1, 1, 0, 0].
Standard Stack
public int[] dailyTemperatures(int[] T) {
int[] res = new int[T.length];
Stack\< Integer\> stack = new Stack\< Integer\>();
for(int i=0;i\< T.length;i++){
//If you find a day with higher temp this will be the ans for all earlier days with lower temp in the stack.
//So pop all of the lower temp days in the stack & add the diff of indexes into the res array.
while(!stack.empty() && T[i] \> T[stack.peek()]){
res[stack.peek()]=i-stack.pop();
}
stack.push(i);
}
return res;
}
(Medium) Design a Stack With Increment Operation
https://leetcode.com/problems/design-a-stack-with-increment-operation/
class CustomStack {
int maxSize; int[] stack; int size=0;
public CustomStack(int maxSize) {
this.maxSize=maxSize;
stack=new int[maxSize];
}
public void push(int x) {
if(size\< maxSize) stack[size++]=x;
}
public int pop() {
if(size\> =1) return stack[--size];
return -1;
}
public void increment(int k, int val) {
if(k\> =size){
for(int i=0;i\< size;i++) stack[i]+=val;
}
else{
for(int i=0;i\< k;i++) stack[i]+=val;
}
}
}
(Medium) Sum of Subarray Minimums
Given an array of integers A, find the sum of min(B), where B ranges over every (contiguous) subarray of A.
Since the answer may be large, return the answer modulo 10^9 + 7.
Example 1:
Input: [3,1,2,4]
Output: 17
Explanation: Subarrays are [3], [1], [2], [4], [3,1], [1,2], [2,4], [3,1,2], [1,2,4], [3,1,2,4]. Minimums are 3, 1, 2, 4, 1, 1, 2, 1, 1, 1. Sum is 17.
Approach: Stack with Class
for every jth position, we should have the minimum subarray.
Playing with some array like A = [1,7,5,2,4,3,9] with j = 6 the minimum of each subarray is B= [1,2,2,2,3,3,9]. Here B[i] represents the minimum value in the subarray A[i,j] where j=6. See it from right to left.
B[3]=2, which means minimum element in A[3,6] is 2.
B[4]=3, which means minimum element in A[4,6] is 3.
For each j we can maintain a stack of (minVal,count) which represent the array B. // stack = [(val=1, count=1), (val=2, count=3), (val=3, count=2), (val=9, count=1)] // for each J we want sum(B), and the result would be the sum of answers for each J.
As we increment j, we will have to update this stack to include the newest element (val=x, count=1). We need to pop off all values >= x before, as the minimum of the associated subarray [i, j] will now be A[j] instead of what it was before.
class RepInteger {
int val, count;
RepInteger(int v, int c) {
val = v;
count = c;
}
class Solution {
public int sumSubarrayMins(int[] A) {
int MOD = (int)Math.pow(10,9)+7;
Stack\< RepInteger\> stack = new Stack();
int ans = 0, dot = 0;
for (int j = 0; j \< A.length; ++j) {
// Add all answers for subarrays [i, j], i \<= j
int count = 1;
//For every J calculate the dot and add to res.
while (!stack.isEmpty() && stack.peek().val \> = A[j]) {
RepInteger node = stack.pop();
count += node.count;
dot -= node.val \* node.count;
}
stack.push(new RepInteger(A[j], count));
dot += A[j] \* count;
ans += dot;
ans %= MOD;
}
return ans;
}
}
}
(Hard) Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Example:
Input: [2,1,5,6,2,3]
Output: 10
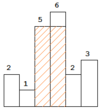
Approach :
1. For every i
If the stack is empty or hist[i] is greater than top of stack, then push ‘i’ to stack.
If this bar is smaller than the top of stack, then keep removing the top of stack while top of the stack is greater.
Let the removed bar be hist[tp]. Calculate area of rectangle with hist[tp] as smallest bar. For hist[tp], the ‘left index’ is previous (previous to tp) item in stack and ‘right index’ is ‘i’ (current index).
- If the stack is not empty, then one by one remove all bars from stack and do step 1 for every removed bar.
public int largestRectangleArea(int[] heights) {
int max=0;
Stack\< Integer\> stack = new Stack\< Integer\>();
int i;
for(i=0;i\< heights.length;i++){
if(!stack.empty() && heights[i]\< heights[stack.peek()]){
//For all rectangles in stack with greater height than ith block,
//calculate area and update max.
while(!stack.empty() && heights[stack.peek()]\> =heights[i]){
int h= heights[stack.pop()];
int w = stack.empty() ? i: (i-stack.peek()-1);
max = Math.max(max, h\*w);
}
}
stack.push(i);
}
while(!stack.empty()){
int h= heights[stack.pop()];
int w = stack.empty() ? i: (i-stack.peek()-1);
max = Math.max(max, h\*w);
}
return max;
}
(Hard) Trapping Rain Water
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.
Example:
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Approach:
- If array element is less than or equal to stack top, add it to stack.
- if it’s greater than the stack top
pop the stack as top, find the distance between the current element and the element at top of stack after popping.
dist=i−st.top()−1
Find the bounded height:
bounded_height=min(height[i],height[st.top()])−height[top]
Add resulting trapped water to ans+=distance×bounded_height.
Note: Here we are adding how much water this bar(which got popped) can trap above itself and between its next greater right & left neighbours.
In the figure, the bar at 6th index which has height of 1, can trap zero water, because its bounded_height is 0.
public int trap(int[] heights) {
Stack< Integer> stack = new Stack< Integer>();
int res=0;
for(int i=0;i< heights.length;i++){
if(!stack.empty() && heights[i]> heights[stack.peek()]){
while(!stack.empty() && heights[stack.peek()]< heights[i]){
int top = stack.pop();
if(stack.empty()) continue;
int d = i - stack.peek()-1;
int h = Math.min(heights[i],heights[stack.peek()]) - heights[top];
res+= d*h;
}
}
stack.push(i);
}
return res;
}
(Hard) Maximum Frequency Stack
Implement FreqStack, a class that simulates the operation of a stack-like data structure.
FreqStack has two functions:
push(int x), which pushes an integer x onto the stack.
pop(), which removes and returns the most frequent element in the stack.
If there is a tie for the most frequent element, the element closest to the top of the stack is removed and returned.
Approach 1:
- Frequency map of elements
- And a map of frequency value to the stack of elements having that. frequency.
Push: O(1) Pop: O(1)
Map< Integer, Integer> freq;
Map< Integer, Stack< Integer >> group;
int maxfreq;
public FreqStack() {
freq = new HashMap();
group = new HashMap();
maxfreq = 0;
}
public void push(int x) {
int f = freq.getOrDefault(x, 0) + 1;
freq.put(x, f);
if (f > maxfreq)
maxfreq = f;
group.computeIfAbsent(f, z - \> new Stack()).push(x); }
public int pop() {
int x = group.get(maxfreq).pop();
freq.put(x, freq.get(x) - 1);
if (group.get(maxfreq).size() == 0)
maxfreq–;
return x;
}
Approach 2:
- HashMap + Priority Queue
Push: O(logn) Pop: O(1)
But this is stupid lol.
LRU
class LRUCache {
class Node{
int key;
int value;
Node pre;
Node next;
public Node(int key, int value)
{
this.key = key;
this.value = value;
}
}
private int maxCapacity;
private int currentCap=0;
private HashMap cache;
private Node head, tail;
public LRUCache(int capacity) {
maxCapacity = capacity;
head = new Node(0,0);
tail = new Node(0,0);
head.next = tail;
head.pre = null;
tail.pre = head;
tail.next = null;
cache = new HashMap();
}
public int get(int key) {
if(cache.containsKey(key)) {
removeNode(cache.get(key));
addNodeatStart(cache.get(key));
return cache.get(key).value;
}
return -1;
}
public void put(int key, int value) {
if(cache.containsKey(key)) {
Node n = cache.get(key);
n.value = value;
removeNode(n);
addNodeatStart(n);
}
else{
Node n = new Node(key,value);
addNodeatStart(n);
cache.put(key, n);
if(currentCap currentCap++;
}
else{
cache.remove(tail.pre.key);
removeNode(tail.pre);
}
}
}
public void removeNode(Node n){
n.pre.next = n.next;
n.next.pre = n.pre;
}
public void addNodeatStart(Node n){
n.next = head.next;
head.next.pre = n;
n.pre = head;
head.next = n;
}
}
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache obj = new LRUCache(capacity);
* int param_1 = obj.get(key);
* obj.put(key,value);
*/


