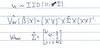Topic 5: Statistical Properties of OLS

Question 1

What is the significance of IID(0,σ₂), and NID(0,σ²)

Answer 1

IID is stands for independent and identical distribution.

NID is a normal, independent and identical distribution.

Question 2

What is the assumed distribution of X in the OLS model.

Answer 2

X is is often assumed in theory not to be distributed, and is treated as a fixed, non-random variable.

This is often a little unrealistic however - in practice it is often assumed that X is simply noncorrelated with the error term. i.e. E(u | X) = 0

Question 3

How do we quantify bias in some estimator?

Answer 3

Bias = E(B^) - B

Where B^ is the estimator, and B is the real value.

Question 4

Prove that the OLS estimate of β is unbias

Answer 4

Question 5

What is the meaning of plim?

Answer 5

Probability limit - returns the convergence of it’s argument when n (the sample size) goes to infinity.

Question 6

What are some proporties of Plim?

Answer 6

Not bothered by non-linear functioms
i.e.

plim(X)=plim(f(X))

Question 7

What is the law of large numbers?

Answer 7

States:

Question 8

How can we prove the OLS estimator is consistant?

Answer 8

By eliminating the second term under plim, which happens as E (u | X) = 0,

Question 9

What is Var(b) and how is it calculated?

What about if E(b) is equal to zero.

Answer 9

This returns the covariant matrix of b, whose diagonal members give the variance of the nth row of b, with remaining entries giving covariances.

This is calculated by E((b-E(b)(b-E(b)^T)

When E(b)=0, This simplifies to:

Var(b)=bb^T

Question 10

What is the formula for the correlation between two variables?

Answer 10

Answer 11

Question 12

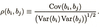
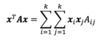
What are the conditions for positive defininess?

Answer 12

• Definite as oppose to semi when diagonals are nonzero.
• Positive when diagonals are positive.

Question 13

Get the formula for the variance of the OLS estimator, given:

Answer 13

Note that the end of the first line is the case because the covariance matrix is symmetric (and so to it’s inverse).

Question 14

What is the variance of a linear function of β, γ =w^Tβ

Answer 14

Var(γ) = w^TVar(β)w

Question 15

How can the variance of a forecasting error be calculated?

Answer 15

Question 16

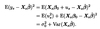
Express the residual vector of an OLS regression in terms of the data population.

What is the expected value of these residuals?

Answer 16

M_Xy = u^ = M_XXβ+M_Xu = M_Xu

Question 17

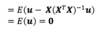
How can the variance of the residuals in OLS be calculated (under homoscedasticity)

Answer 17

Question 18

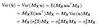
Give an equation that relates the leverage of an individual point with the residual of that point.

Answer 18

Where h_t is the t^th diagonal element from P_X.

As h_t is a measure of the points leverage, this means that the higher the leverage of a point, the lower the variance of it’s residual.

Question 19

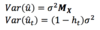
What is the result of the following, and what does this suggest about an unbias estimator of error variance?

Answer 19

Question 20

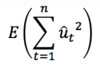
Show what happens to error and variance when a model is overpecified as:

y = Xβ + Yγ + u

Answer 20

Note (Variance is higher unless X is orthogonal to Z)

Question 21

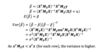
What is the formula for adjusted R²?

Answer 21

Uses accurate estimates of error.

Question 22

What is White’s method for estimating error under heteroscedasticity?

Answer 22