Topic 13: Risk, Portfolio Diversification & Shocks

Question 1

Demonstrate on a graph how diminishing marginal utility causes risk aversion. Show the price this agent would be willing to pay for insurance that eliminates risk.

Answer 1

Due to the concave shape of the utility function U(Y), the expected utility from a 50% lottery (with Y₀-u Y₀+u as prizes) is only U(Y_C) (the average of U(Y₀-u Y₀+u)). This is lower then the utility recieved from the average income (E(Y)), Y₀.

As a result, consumers would be willing to pay up to Y₀+u-Y_C in the good years for insurance that bumps income to Y_C in the bad years, where Y_C-Y₀ is the risk premium, or a monopolostic insurers profits.

Question 2

How can we measure the risk aversion of a utility function?

Answer 2

With the arrow pratt coefficient of relative risk aversion R(Y) = ^{-Y U’‘(Y)}/_U’(Y).

A unitless parameter that changes along the utility function as Y increases. Zero for a straight line as U’‘(Y) = 0.

Question 3

With what formula can we calculate U(Y_C), gained from a taylor expansion?

Answer 3

U(Y_C) = EU(Y) ~= U(Y₀) + ¹/₂u²U’‘(Y₀)

(where u is the deviation of the lottery outcomes from the expected outcome).

Question 4

With what equation can we approximate the risk premium?

How about P_y/Y₀

Answer 4

p ~= ¹/₂u²U’‘(Y₀)/U’(Y₀)

p_y/E(Y) ~= ¹/₂R (SD(Y)/E(Y))²

p/E(Y) ~= ¹/₂Rσ_Y²

Where σ_Y is the coefficient of variation.

Question 5

Following from ρ/E(Y)~= ¹/₂Rσ_Y²

Give the equation for Y_C

Answer 5

ρ/E(Y) = ¹/₂Rσ_Y²

ρ=¹/₂RVar(Y)/E(Y)

Yc = E(Y) - ρ

Y_C= E(Y)-¹/₂RVar(Y)/E(Y)

Question 6

How would be describe the risk adversness of R = 1, 2 & 4?

Answer 6

R=1 - Very lightly risk adverse.

R=2 - Risk adverse.

R=3 - Very risk adverse.

Question 7

What is the equity premium puzzle?

Answer 7

The risk premium on private assets (relative to government debt) is much larger then would be expected given an R value of 2 - calculated from psychological experiments.

Question 8

How might we explain the equity puzzle?

Answer 8

• It is possible that the estimates of R=2 don’t scale up from the low lotteries used in the experiments to the volumes of the lotteries in finance.
• Portfolio holder idiosyncratic risks -enemployment, credit constraints mean a higher value on liquidity
• Imperfect imformation, makes prices more volatile, which seems to suggest risk aversion.
• Narrow framing- households focus on one risky venture at a time, and don’t see the gains from diversification.
• Loss aversion - aversion to downside risks is disproportionately high.

Question 9

A household has assets of 2mil, that if invested in teasury bonds guarentee a 5% return. Alternatively, an investment in stocks gives the following schedule of returns. Given R = 2, calculate the certainty equivilent of the stock investment and indicate the housholds choice of asset.

Rate of Return | Probability

4% | .25

5% | .25

5. 5% | .25
6. 5 | .25

Answer 9

First, calculate the actual returns

Y_Tbond=100000

80000, 100000, 110000, 150000

E(Y_stocks) = 110000

SE = sqr(Var(Y_stocks)) = sqr(Sum(p(Yi) x (Yi-E(Y)² ) = 25495

Coefficient of variation = 25495/110000=0.232

p/E(Y) = .5Rσ_Y² = 0.232²=5.37%

p = $5909, Y_C= $104091

Question 10

Consider a household that allocates wealth between portfolios such that it’s income is determined from the following equation.

How is the variance of the portfolio calculated?

What if the portfolio is just two assets, with the same E(r) & variance?

Answer 10

Var(X + Y) = Var(X) + Var(Y) + 2Cov(X,Y)

Question 11

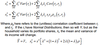
Given a two asset portfolio where E(r_i) & Var(r_i) is identical:

Find the optimal portfolio, and it’s variance.

Answer 11

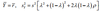
To maximise, we set ^dsy2/_dλ=0

0=s²(4λ(1-ρ)-2(1-ρ))=4λ(1-ρ)-2(1-ρ),

4λ=2, λ = .5

so s_Y²= s²(1+ρ)/2

Note that if ρ < 1, then s_Y² < s2

Question 12

Show how a portfolio with two assets, one riskier and with a greater return then the other can be constructed, with regards to E(Y) and s_Y

Answer 12

Question 13

From = E(Y)-1/2RVar(Y)/E(Y)

How can we construct a utility curve (where U(Y_C))

Answer 13

We must keep Y_C constant.

So we rearrange so that

E(Y) = Yc + Rs_Y²/2E(Y)

We can then conclude when s_Y increases, E(Y) must increase. We can then graph

Question 14

How can we construct our portfolio possibility frontier when we have two assets, and an additional risk free low return asset. Give equations that show the return on the portfolio.

Answer 14

E(Y) = λr_{s +} (1 - λ)r_r where r_s = safe return r_r = risky return

s_y = (1-λ)s_r

We can then subsitute for lambda, so we get

E(Y) = rs + s_y(r_r - r_s)/s_r

We might consider the s_r of the utility maximising portfolio without the safe asset. Then the above linear equation is our new portfolio frontier.

Question 15

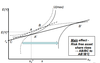
Show the effects of a shock that aligns (correlates risk), given a risk free asset.

Answer 15

ρ goes up, so (see graph)

Importantly, this recessiony shock causes a move to T bonds, big flight from the private investment market.