Topic 11: The market for domestic savings

Question 1

In the Fisher savings model, what is the household allocation problem?

Answer 1

To allocate consumption between the two periods C₁ & C₂, by choosing the amount of savings in C₁, so as to maximize the present value of its utility in the first period. We can define β as 1 / 1 +δ where δ is the rate of discount for the household.

U = U(C₁) + βU(C₂)

where: 0 < β < 1, U’(C) > 0, U’‘(C) < 0

Question 2

Construct the inter-temporal budget constraint in the Fisher savings model.

Answer 2

P₂C₂ = P₁S₁(1+i)+P₂Y₂

P₂C₂ = (P₁Y₁ - P₁C₁)(1+i) P₂Y₂

P₁(1+π)C₂ = (P₁Y₁ - P₁C₁)(1+i) + P₁(1+π)Y₂

C₂ = (Y₁ - C₁)(1+i)/(1+π)

C₂ = (Y₁ - C₁)(1+r) + Y₂

Question 3

Graph the budget constraint in the Fisher model. Indicate the slope and describe how the curve would shift with a change in r.

Answer 3

The budget line is anchored at A, where there is no saving. An increase in r causes the slope of the BC to increase, so this would make the curve rotate clockwise, staying on the point A.

Question 4

In the fisher model, what is the effect of a rise in the real interest rate?

Answer 4

The rise causes an income and substitution effect. The income effect raises C₂ unambiguously. The effect on C₁ is ambiguous, and depends on the elasticity of inter-temporal substitution between C₁ & C₂.

Question 5

Under the Fisher model, what would the domestic savings supply curve look like if consumption between periods are perfect complements? What if they are strong substitutes? Which is more likely in real economies?

Answer 5

An increase in r necessarily means an equal increase in C₁ & C₂.

As C₁ increases savings decrease, so the savings supply curve is downward sloping.

If they are strong substitutes, then C₁ would likely decrease, and so the savings supply curve would slope upwards. This is the more frequently observed scenario.

Question 6

What is the inter temporal Euler Equation?

Answer 6

U’(C₁) / U’(C₂) = (1+r) β

This means at the optimal level of consumption, the country can’t gain from shifting consumption between period 1 & 2.

Can also be written

βMU₂/MU₁ = MRS = 1/1+r = MRT

Question 7

What is the situation in the Fisher model where the discount rate is equal to the real interest rate? What is the marshellian demand curve for savings in this situation?

Answer 7

Then as U’(C₁) = (1+r) β U’(C₂),

U’(C₁) = U’(C₂)

Therefor C₁ = C₂ and there is perfect consumption smoothing.

From the budget constant, we get S₁ = Y₁-Y₂ / (2 + r)

Question 8

In the Fisher Model under consumption smoothing, How do permenant changes in output affect the savings rate?

How about a temporary fluctuation?

Answer 8

• Permenant changes do not alter the savings rate
• Temporary changes will alter the savings rate because households will consumption smooth

Question 9

What is the equation for the inter-temporal elasticity of substitution?

What are the implications for the savings supply curve if it is zero, one, or over one.

Answer 9

It is the elasticity of C₂/C₁ and (1+r), ie, the percentage change in C₂/C₁ given a change in (r+1).

When σ = 0, there is perfect compliments.

When σ = 1, we have cobb douglas utility, where the income & substitution effects cancel. (there is no change of savings with change in r)

When σ > 1, we have strong substitues, where the subsitution effect dominates the income effect, so an increase in r increases savings.

Question 10

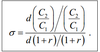
What is the Arrow-Pratt coefficient of relative risk aversion (R)?

How can we express it relative to the inter-temporal elasticity of substitution?

Answer 10

It is the inverse of the inter-temporal elasticity of substitution.

It’s also a measure of the curvature of the utility function that determines risk preferences in portfolio management.

Question 11

What is the equation then for our savings supply?

Answer 11

S_D = S_D (Y_N (+),Y_F^E (-), G(-), r(+))