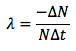Topic 13 - Quantum physics and nuclear physics

Question 1

What is the photoelectric effect?

Answer 1

When electromagnetic radiation is directed onto a clean surface of some metals, electrons are ejected.

Question 2

What are photoelectrons?

Answer 2

Electrons ejected due to the photoelectric effect from the surface of some metals

Question 3

What kind of EM waves can produce the photoelectric effect?

Answer 3

• Under suitable conditions, visible light, X-rays, and gamma rays
• Most often ultraviolet radiation is used together with a zinc plate

Question 4

What are the key features of the photoelectric effect?

Answer 4

1. If the intensity of the radiation is increased more photoelectrons are being released every second
2. There is no time delay between the radiation reaching the metal surface and the emission of photoelectrons → release is instantaneous
3. The effect can only occur if the frequency of the radiation reaches a certain minimum value known as the threshold frequency, f₀
4. For a given incident frequency the effect occurs with some metals but not with others (due to different f₀ of metals)

Question 5

What is a photon?

Answer 5

A packet of energy in electromagnetic radiation (instead of continuous waves)

Question 6

What is the energy carried by each photon?

Answer 6

E = hf

where

h = Planck’s constant,

f = frequency of the radiation

Since c = fλ:

Question 7

Why can’t the wave model of light be used to explain the photoelectric effect?

Answer 7

Because

1. There would be a delay before the effect begins after the wave hits the surface
2. Radiation of any frequency would cause the photoelectric effect if the intensity is high enough

Both are wrong

Question 8

Outline the Einstein model of photoelectric effect

Answer 8

• Explains the effect using the concept of photons
• When a photon interacts with an electron, it transfers all of its energy to that electron
• A single photon can only interact with a single electron
• Increasing the intensity of radiation only increases the no. of photoelectrons, not their energies
• Some of the energy of the photon is used to overcome the attractive forces of the electron
• The remaining energy is transferred to the kinetic energy of the photoelectron

Question 9

What is work function, ϕ?

Answer 9

• The energy required to remove different electrons is not always the same
• There is a minimum amount of energy needed to remove an electron, called the work function
• Different metals have different values for their work function

Question 10

What is the relationship between a photon’s energy, hf, and the work function, ϕ, of a metal?

Answer 10

hf < ϕ

• Less energy than the work function
• The photoelectric effect cannot occur

hf₀ = ϕ

• Exactly the same energy as the work function
• The effect occurs and a photoelectron is released, but the electron will have zero kinetic energy

hf > ϕ

• More energy than the work function
• The effect occurs

Question 11

What is Einstein’s photoelectric equation?

Answer 11

hf = ϕ + E_max

hf = hf₀ + E_max

where

hf = energy carried by photon,

ϕ = work function,

E_max = maximum kinetic energy of photoelectron

hf₀ = ϕ

Question 12

What is the stopping potential, V_s, in the Einstein model?

Answer 12

The potential on the anode needed to just stop all photoelectrons reaching it

E_max = eV_s

Question 13

How can Einstein’s photoelectric equation be re-written with the help of stopping potential?

Answer 13

hf = ϕ + eV_s

or

hf = hf₀ + eV_s

Question 14

What is the de Broglie hypothesis?

Answer 14

All moving particles have a wave-like nature. The wavelength of a moving particle is related to its momentum:

Question 15

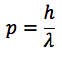
What is meant by matter waves?

Answer 15

Matter can also behave like a wave (photons and electrons)

Question 16

How did the Davisson-Germer experiment prove de Broglie’s hypothesis?

Answer 16

• Since electrons are particles that behave like waves, they should also be diffracted like light

boom

• They were diffracted

Question 17

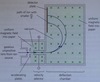
How can the emission spectrum of an atom be investigated?

Answer 17

Atoms emit electromagnetic radiation when excited by heating or passing an electric current through its gas

• A spectrometer is used
• A beam of light from excited gaseous atoms is passed through a lens via a slit to a second lens and then to a prism
• The prism separates the spectral lines, which can be observed and measured using an eyepiece

Question 18

How can the absorption spectrum of an atom be investigated?

Answer 18

• White light is shone through a sample of a gaseous element (at low pressure and temperature)
• The light that emerges has some wavelengths missing
• These bands in the spectrum are the element’s characteristic wavelengths
• The position of these bands is the same as the position of the lines in teh emisison spectrum

Question 19

Explain how energy is quantized in atoms

Answer 19

• Electrons can only exist in certain energy levels
• They behave like stationary waves fitted into the circumference of the orbit
• A free electron at n = ∞ has zero energy
• n = 1 has the lowest energy
• The values are negative because energy is lost as the electron moves closer to the nucleus
• For an electron to move between energy levels, energy must be absorbed or given out
• Thermal energy raises some electrons to an excited state
• An excited electron will quickly fall back to a lower energy level

Question 20

How do atomic spectra provide proof for the quantization of energy in atoms?

Answer 20

• When electrons fall from their excited state, the downward transition corresponds to the emission of a photon whose energy is the same as the energy difference between the energy levels:

hf = E₂ – E₁

• Similarly, photons can only be absorbed if their energy corresponds to the energy difference between two energy levels
• Further away from the nucleus, the energy levels become closer and closer and show convergence of lines at high frequency

Question 21

How is the electron in a box model used to rationalise the atomic energy levels?

Answer 21

• The model uses the idea of the electron behaving as a wave to explain why the energy levels in atoms are quantized
• Electorn is confined in a small region between two walls
• If the electron is a wave, it must show boundary conditions (standing wave)
• The wave has nodes and antinodes
• The walls of the box must always be nodes
• The waves must have a whole number of half wavelengths within the box
• The wavelength of the electron wave is determined by the size of the box

Question 22

How is the wavelength and energy of an electron given by the electron in a box model?

Answer 22

m_e = mass of electron

n = the integer in the box (idk?)

L = length of the box

Question 23

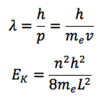
What is the Schrödinger model of the hydrogen atom?

Answer 23

• The model assumes that electrons in the atom may be described by wavefunctions, Ψ(x, t)
• The electron has an undefined position
• The square of the absolute value of the amplitude is a measure of the electron density (probability distribution) in a region of space:

|Ψ(x, t)|²

Question 24

What does the Heisenberg uncertainty principle suggest?

Answer 24

That it is impossible to know both the momentum and the displacement at the same time: the more accurately we know the speed of the electron (the smaller the ∆p), the less we know about where it is (the larger the ∆x)

Relationship can be written as:

Question 25

What is another relationship besides momentum-displacement that the Heisenberg uncertainty principle applies to?

Answer 25

Energy-time:

Question 26

What is the relationship between de Broglie wavelength and Heisenberg uncertainty principle?

Answer 26

If a particle has a uniquely defined de Broglie wavelength, its momentum will be known precisely, but there is no knowledge of its position.

Question 27

How can the radii of nuclei be estimated from charged particle scattering experiments?

Answer 27

• The radius of a nuclei can be calculated by how close an alpha particle gets to the nucleus during its interaction, before it is repulsed
• At this point all of its kinetic energy has been converted into electrical potential energy

Question 28

What is the equation for calculating the radius of a nucleus?

Answer 28

Question 29

How can the masses of nuclei be measured with a Bainbridge mass spectrometer?

Answer 29

• The particles are in a vacuum to avoid collisions with air
• The ions are accelerated
• Only a narrow beam of ions at the same velocity are allowed to get into the deflection chamber
• The radius of the circle of each ion’s path will only depend on the mass of the ion → larger mass will travel in a larger circle

Question 30

What provides evidence for the existence of nuclear energy levels?

Answer 30

• Alpha particles produced by decay have discrete energies
• Gamma ray spectra are discrete

Question 31

What are the two types of beta decay?

Answer 31

1. Beta-negative decay
2. Beta-positive decay

Question 32

What is the process of beta-negative decay?

Answer 32

• A neutron changes into a proton with the emission of an electron and an antineutrino

Question 33

-What is the process of beta-positive decay?

Answer 33

• A proton changes into a neutron with the emissino of a positron and a neutrino

Question 34

What is the decay constant?

Answer 34

The probability per unit time that any particular nucleus will undergo decay

N = number of undecayed nuclides in the sample

Question 35

What is the activity, A, of a radioactive source?

Answer 35

The number of nuclei decaying per second (same as the rate of decay)

Measured in becquerels (Bq) = 1 decay per second

Question 36

What is the number of undecayed nuclei after time t?

Answer 36

N = N₀e^–λt

N₀ = initial number of undecayed nuclei

Question 37

How is the activity related to the number of initial undecayed nuclei?

Answer 37

A = λN = λN₀e^–λt

Question 38

Derive the relationship between decay constant and half life

Answer 38

Question 39

How can the half-life be measured in isotopes with long half-lives?

Answer 39

• If the activity can be determined, then the half-life can be calculated too

A_r = relative atomic mass

N_A = Avogadro’s constant

Question 40

How can the half-life be measured in isotopes with short half-lives?

Answer 40

• Can be measured directly
• Measuring the count rate over a short period of time
• Count rate is proportional to activity

A = A₀e^–λt

lnA = lnA₀ – λt