Topic 1: key concepts and revision

Question 1

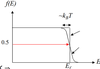
Describe the fermi dirac distribution using a sketch to support your answer

Answer 1

• The fermi dirac distribution takes the form f(E) = 1 / e^(E-Ef)/kT + 1 and describes all available states in a material and whether they are occupied at a given temperature (not whether they are allowed or not)
• For a metal at 0K electrons populate energy levels up to the Fermi energy, E_f
• When T > 0K E_f is the probability of occupancy at 0.5

Question 2

• Why does the graph shape change at finite temperature?

Answer 2

• As temperature increases higher energy state become occupied
• Therefore, states below E_f have less chance of being occupied

Question 3

What is a hole in term of electronics?

Answer 3

• Used to describe properties of a vacant electron state in an otherwise full band

Question 4

• How do energy levels differ in semiconductors compared with metals?

Answer 4

• In a metal, the conduction band (CB) ? is partially occupied up the fermi level
• In semi-conductors the fermi level lays between the fully occupied valence band (VB) and the first unoccupied band, the conduction band (CB) in an energy gap

Question 5

• What is the vacuum level?

Answer 5

• Area outside of solid surface/molecule where electron is free
• Make sure to draw this on diagrams as well as energy on y axis

Question 6

• Define conductivity

Answer 6

• σ =J/E where J is current density and E is electric field

Question 7

• Define conductivity in terms of electrons/holes

Answer 7

• σ =n_ppµ_p + n_eeµ_e
• n_p/e -desnity of holes/electrons
• p/h – charge on a hole/electron (+/- 1.6E-19 C)
• µ_p/n – hole/electron mobility (cm² V^-1 s^-1)

Question 8

Graphene is a semiconductor, but equally as conductive as many metals, why is this?

Answer 8

• Graphene has a low density of electrons but very large mobility
• Metals are the opposite to this

Question 9

• How can hole/electron density be increased?

Answer 9

Doping; incorporate impurity states in to lattice that can pull electrons out of VB – hole/ inject electrons in to CB – electrons

Question 10

• How does the size of materials affect its properties?

Answer 10

• As a material is shrunk down, the proportion of atoms at the surface becomes more significant due to an increase in SA/V ratio
• Leads surfaced environment properties to dominate functionality of device more.
• And example of a structure that uses this would be carbon nanotubes

Question 11

• What is charge transfer doping and what are its advantages over conventional doping?

Answer 11

• Molecular adsorption of a molecule on to a surface where charge transfer occurs at the frontier molecular orbitals between the two species
• This does not disrupt the lattice, therefore not degrading the mobility as we have no need to break any bonds to introduce an impurity.

Question 12

• Why is conductance (G) used in nanotechnology rather than conductivity (σ)?

Answer 12

• G = IV is a measure of ease of flow of current along a given path (i.e. through a specific component)

Question 13

• G is only … under very specific conditions, when transport is … ,
• Meaning there is no … of electrons that move through material

Answer 13

• G is only quantized under very specific conditions, when transport is ballistic,
• Meaning there is no scattering of electrons that move through material

Question 14

• Describe and explain the following graph

Answer 14

• Gradient near x/y axis gives conductance of each molecule (G = I/V)
• This would indicate molecule ½ are highly conjugated and 3 is saturated as expected
• The amount of current for a given voltage is much higher due to delocalised p orbitals.

Question 15

• What is the work function (ϕ)?

Answer 15

• The energy required to eject an electron from the fermi level up and out to the vacuum level.

Question 16

• How can the came material have a different number of work functions?

Answer 16

• Work function will be different depending on which crystal face is exposed (i.e. Ag 100 WF will differ from 111 due to a different arrangement of atom sat the surface)

Question 17

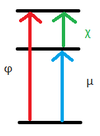
• Describe the components of the work function

Answer 17

• Chemical potential (µ) – associated with atom type
• Surface potential (χ) – depends on crystal face/ arrangement of atoms on surface.

Question 18

Explain how does the surface potential (SP) affects the WF

Answer 18

• Electron density has a probability to spill outside of solid at finite temperature
• This causes a dipolar layer to form at the interface that an ejectin electron must travel through.
• This causes an increase in potential energy.

Question 19

• What is the pushback/pillow effect?

Answer 19

• An absorbed molecule (even only weakly physisorbed) can push electrons spilling into the vacuum back in to the solid
• Coulombic repulsion and Pauli exclusion between electron densities of adsorbate and surface lead to compression of metal surface dipole tail by adsorbate.
• However, this is not a charge transfer process

Question 20

Describe the charge transfer interaction of chemisorbed surface adsorbates and how it affects the work function

Answer 20

• Change in WF not due to push back effect
• Ionisation voltage is less than the metal WF in donor adsorption from high energy HOMO
• Reverse is true for acceptors, with charge transfer to low energy LUMO

Question 21

• Complexity at …-…interfaces makes is difficult to predict extent of … between E_f in metal and … molecular orbitals when charge transfer due to adsorbate moves the fermi level of the metal, making prediction difficult.

Answer 21

• Complexity at metal-organic interfaces makes is difficult to predict extent of alignment between E_f in metal and frontier molecular orbitals when charge transfer due to adsorbate moves the fermi level of the metal, making prediction difficult.