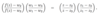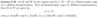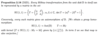The Geometry of Holomorphic Maps

Question 1

Define conformal at z₀.

Answer 1

A (real differentiable) map f : 𝑅 ➝ ℂ on a region 𝑅 ⊆ ℂ is conformal at z₀ if it is angle and orientation preserving at z_0.

Question 2

Finish the following proposition

Answer 2

Question 3

Finish the corollary: Conformal maps take orthogonal grids (in the x-y plane) to … ?

Answer 3

Orthogonal grids (in the u-v plane).

Question 4

Let f = u + iv be a holomorphic function and let Ɣ and Ɣ ̃ be two paths given by the level curves u(x, y) = C₁ and v(x, y) = C₂ respectively (for C₁, C₂ real constants). Then what sets (whenever f′(z) ̸= 0)do the paths Ɣ and Ɣ ̃ form?

Answer 4

Orthogonal set in the x-y plane

Question 5

Define a biholomorphic map from 𝑅 to 𝑅’.

Answer 5

We call a holomorphic map f on a region 𝑅 a biholomorphic map from 𝑅 to 𝑅’ = f(𝑅) if:

1. 𝑅’ is a region
2. f is one-to-one and the inverse map f^-1:𝑅’ ➝ 𝑅 is also holomorphic

Question 6

What symbol do you use to show two regions 𝑅 and 𝑅’ are biholomorphic.

Answer 6

f : 𝑅 ⥲ 𝑅’

Question 7

What is the Lemma about the automorphism group of 𝑅.

Answer 7

Question 8

Define simply connected.

Answer 8

A region 𝑅 is simply-connected if every closed path Ɣ in 𝑅 (that is Ɣ(0) = Ɣ(1)) can be “continuosuly shrunk” to a point in 𝑅. Heuristically this means 𝑅 has no holes.

Question 9

Is ℂ٭ or ℂ\ℝ_≤0 simply connected?

Answer 9

ℂ\ℝ_≤0

Question 10

What is the Riemann mapping theorem.

Answer 10

Every simply connected region 𝑅 ≠ ℂ, there exists a biholomorphic map f:𝑅 ⥲ B₁(0)

Question 11

Define a Möbius transformation.

Answer 11

Question 12

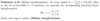
Why do we exclude matrices for which det(T) = 0 in Möbius transformations?

Answer 12

M_T is constant if det(T) = 0

Question 13

If k = sqrt(|det(T)|) show that we can scale any Möbius transformation so that det(T) = ± 1.

Answer 13

Question 14

What is the Lemma about the set of Möbius transformation forming a group under composition.

Answer 14

Question 15

Prove the following Lemma.

Answer 15

Need to do - see sheet 5

Question 16

What is the symbol for the extended complex plane?

Answer 16

Question 17

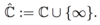
What are three algebraic operations on ℂ that are extended to ℂ^∼ ?

Answer 17

Question 18

What do these four properties show.

Answer 18

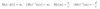
That the

Question 19

What is the propositiong about circles, line and Möbius transformations?

Answer 19

Möbius transformations map circles or lines to circles or lines

Question 20

What are the three different maps between circles and lines with Möbius transformations?

Answer 20

1. Circles not through the origin go to tcircles not through the origin
2. Circles through the origin go to lines not through the origin
3. Lines through the origin go to lines through the origin

Question 21

How can you find a map from ℍ to ⅅ by writing ℍ in a clever way?

Answer 21

Question 22

What is the Mob transformation to take the upper half plane to the unit disc?

Answer 22

Question 23

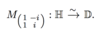
What is the inverse of this map called?

Answer 23

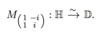
Caley Map

Question 24

How is the Caley Map denoted?

Answer 24

Question 25

Finish the Lemma: If a Möbius transformation has three or more fixed points in … ?

Answer 25

Question 26

What is the proposition about how three points determine a Möbius transformation?

Answer 26

Question 27

Prove the following proposition.

Answer 27

Question 28

What is the corollary about find the Möbius transformation using their cross-ratios?

Answer 28

Question 29

What is the general strategy to find a Mob trans from how it acts on three points?

Answer 29

Rearrange the following equation.

Question 30

What is the general strategy to find the imagine of a region 𝑅 under a Mob trans M_T?

Answer 30

Question 31

What does Mob(𝑅) stand for?

Answer 31

The set of all Mob trans from a region 𝑅 to itself.

Question 32

Finish the following Lemma.

Answer 32

Question 33

What is the H2H proposition?

Answer 33

Question 34

Prove the following proposition.

Answer 34

Question 35

What is the D2D proposition?

Answer 35

Question 36

What is the corollary D2D٭?

Answer 36

Question 37

What is the H2D proposition?

Answer 37