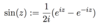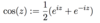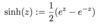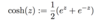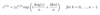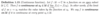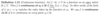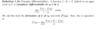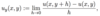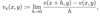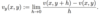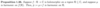Complex Plane and Functions Flashcards
Define a complex number.
A complex number is quantity of the form z = x + iy, where x, y are real numbers and i is the imaginary unit.
What do we denote the set of complex numbers by?
ℂ
What do we denote the real and imaginary part of a complex number by?
If z = x + iy:
- Re(z) = x
- Im(z) = y
When dividing two complex numbers what do you have to multiply it by?
The complex conjugate of the denominator, ẑ = x - iy
What is the complex conjuagte of z?
ẑ = x - iy
What algebraic properites of ℝ don’t hold in ℂ? And why?
Any inequalitie of the form <, > etc. because ℂ isn’t “ordered”
What diagram do we draw complex numbers on?
Argand diagram
What does complex conjugation look like in an Argand diagram?
Reflection in the real axis
What is the modulus of z?
What is the Lemma about four of the useful and basic properties of complex numbers?
In what other types of coordinates can you write compelx numbers?
Polar coordiantes
What is the argument of z?
When written in polar form, it is θ
What are the two ways to write a comlex number in polar form?
- z = r(cosθ + i sinθ)
- z = reiθ
What is arg(z) only defined up to?
Multiples of 2π
Define the principle value of arg(z).
The principle value of arg(z) is the value in the interval (-π, π]
How is the principle value of arg(z) denoted?
Arg(z)
What does Re(z) look like on an argand diagram?
Projection onto the real axis
What does Im(z) look like on an argand diagram?
Projection onto imaginary axis
Finish the Lemma: Geometrically, multiplication in ℂ is given by a … ?
Prove the following Lemma.
What is de Moirve’s theorem?
(cos(θ) + isin(θ))n = cos(nθ) + isin(nθ)
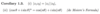
What are three additional properties of the modulus |.|?
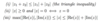
What are three additional properties of the argument?
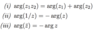
Define a complex exponential function.
What is the propositiion about five properties of the complex exponential function?
What does exp(2πi) equal?
exp(2πi) = 1
What does exp(πi) equal?
exp(πi) = -1
What is Euler’s famous formula?
exp(πi) = -1
What equation shows that the complex exponential function is 2πi periodic?
exp(z) = exp(z + 2kπi) ∀ k ∈ ℤ
What does the following corollary imply?
exp is determined entirely by the values it takes on any horizontal strip of width 2π in the complex plane
Define sin(z) in terms of complex exponentials.
Define cos(z) in terms of complex exponentials.
Define sinh(z) in terms of complex exponentials.
Define cosh(z) in terms of complex exponentials.
What is a trig formula that relates cosh and cos?
cosh(iz) = cos(z)
What is a trig formula that relates sinh and sin?
sinh(iz) = isin(z)
How are the solutions to ez = w written?
z = ln(w) + i(Arg(w) + 2kπi)
Prove the following Lemma.
Define a logarithm of w.
Any solution z of the equation ez = w (with w ∈ ℂ٭) is called a logarithm of w and it is denoted log(w)
Define the kth branch of log(w).
For any fixed k ∈ ℤ, we call the logk : ℂ \ ℝ≤0 ➝ ℂ defined by:
logk(w) = ln|w| + iArg(w) + i2kπ,
the kth branch of log(w).
Define the principle branch of log(w).
When k = 0, we call the function Log(w) = log0(w) the principle branch of log(w), that is, Log : ℂ \ ℝ≤0 ➝ ℂ and:
Log(w) = ln|w| + iArg(w)
The principle branch, Log agrees with what on the real line?
The natural logarithm, ln
What are three properites when using any given branch of logarithm?
- elogz = z for any z ∈ ℂ \ ℝ≤0, but
- in general, log(zw) ≠ log(z) + log(w)
- in general, log(ez) ≠ z.
Define complex powers.
For any branch of log, we define zw (for z ∈ ℂ \ ℝ≤0) by
zw = exp(w logz)
What formula can you use to find all roots of z?
What dimension would graphs of complex-valued functions be?
4 dimensions
Define an open ball of radius r centred at z0.
Define a closed ball of radius r centred at z0.
Define when a subset is open.
Define when a subset is closed .
What is the (open) unit disc? And how is it denoted?
B1(0), 𝔻
Is ℂ open or closed?
Open
Is ∅ open or closed?
Open
Is the set ℂ \ ℝ≤0, on which log and complex powers are defined open or closed?
Open
Do open or closed sets contains their edges/boundaries?
Closed
Define what is meant by converges to the limit z0.
Define what is meant by tends to w ∈ ℂ as z tends to z0.
What is another way to write
Complete the following Lemma
Define what is meant by continuous at z0 ∈ U and therefore continuous on U.
How can you rewrite this definition to be in terms of open balls?
How did we make Log(z) a continuous function?
By fixing the domains
Define (complex) differentiable at z0 ∈ U.
Define derivative of f at z0.
What is the difference between the direction of limits in complex limits compared to real?
In complex the limit exists from every direction where as real limits only exist to the left and right of the real number line.
Finish this sentance: if a function f is complex differentiable at z then .. ?
it is continuous at z.
When calculating whether a function is complex differentiable using the limit what is one thing you have to do differently to if it was a real functions ? And why?
Approach z from two different direction, real and imaginary. And then check that they are the same.
Write ux(x, y) in terms of limits.
Write uy(x, y) in terms of limits.
Write vx(x, y) in terms of limits.
Write vy(x, y) in terms of limits.
What is the proposition about the Cauchy-Riemann equations?
Using the Cauchy-Riemann equations what are the four ways you can write the complex derivative of f(z0)?
Prove the following proposition.
If f is complex differentiable this implies f is real differentiable and what else?
That the C-R equations will hold
What is the thereom that uses the C-R equations to prove something is complex differentiable?
Define holomorphic on U.
A function f:U ➝ ℂ defined on an open set U ∈ ℂ is called holomorphic on U if it is complex differentiable everywhere in U.
Define holomorphic at z0 ∈ U.
We say that f is holomorphic at z0 ∈ U if it is holomorphic on some open ball Bε(z0)
Define a path.
A path (from a ∈ℂ to b ∈ℂ) is a continuous function Ɣ[0,1] ➝ ℂ such that Ɣ(0) = a and Ɣ(1) = b.
Define piecewise smooth.
A path is piecewise smooth if it is continuously differentiable at all but finietly many points.
Define path connected.
We say a subset U of ℂ is path connected if for every pair of points a, b ∈ U, there is a piecewise smooth path from a to b such that Ɣ(t) ∈ U for every t ∈ [0,1].
Define a region.
A region, R is an open, path-connected subset of ℂ.
What is the zero derivative therom?
Prove the zero-derivative thereom.
What is the proposition about the Laplace equations?
What are the two Laplace equations?
Prove the following propostion about the Laplace equations.
Define a harmonic function.
A real-valued function U:𝑅 ➝ ℝ (defined on region 𝑅 ⊆ ℂ) is harmonic on 𝑅 if U is tqice continuously differentiable and Uxx + Uyy = 0
What is the proposition about the harmonic conjugate?
How do you find harmonic conjugates?
- Partially integrate with respect to one variable (y)
- Make a guess of the solution which includes some function independent of the variable you just integrated by
- Differentiate and use the other C-R equations to find the remaining function
What is the Dirichlet Problem?
With the Dirichlet problem what does Ṝ stand for (minus the dot underneath)?
Ṝ = 𝑅 ∪ ∂𝑅
What does ∂𝑅 stand for in the Dirichlet boundary problem?
The boundary of some region 𝑅.
Finish this proposition: Suppose f:𝑅 ➝ ℂ is holomorphic on a region 𝑅 ⊆ ℂ, and suppose μ is harmonic on f(𝑅). Then …
μ∼ = μ ◦ f is harmonic on 𝑅.
Prove the following proposition.
Need to do - see sheet 3, Q6
