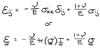Test 2 Material Flashcards
The Conservation of Mass states that…
The mass of any subbody E0 must remain unchanged by the deformation:
m(E0) = m(E)
The Balance of Linear Momentum states that…
The rate of change of momentum is equal to the applied force.
What is the local expression of the conservation of mass?
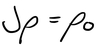
What is the global expression of the Balance of Linear Momentum?

What is the equation for Cauchy’s relation?
(Hint: it relates stress, traction, and normal vector)
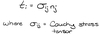
What is the equation for the local form of the balance of linear momentum?
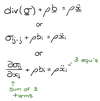
What is the local form of the balance of linear momentum for static problems?
(Hint: these are the equilibrium equations)
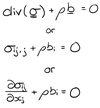
The balance of angular momentum implies that the Cauchy stress tensor is…

The symmetry of the stress tensor has 3 consequences. What are they?

Give the equation for the stress (traction) vector given a stress tensor and a normal vector.
How would you find the normal component of this stress vector?
How would you find the shear component of this stress vector?

Write the equation of the Cauchy stress tensor with respect to deviatoric and hydrostatic (spherical) stress.

Write the equation for hydrostatic (spherical) stress (pressure).
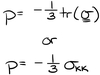
Write the equation for the deviatoric stress tensor.

What is a stress state called where the deviatoric stress is zero?
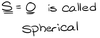
Give the equation for Hooke’s Law for a linearly elastic material in terms of the elasticity tensor (also called the tensor of elastic moduli or the stiffness tensor).
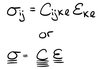
In linear elasticity, what do we assume about the reference versus the deformed configuration?
In linear elasticity, we assume that the reference configuration is indistinguishable from the deformed configuration.
As a fourth order tensor, the elasticity tensor, C, has 81 components. However, to be consistent with definitions and properties of continuum mechanics, there are two constraints (in particular) that limit the number of independent components of C. What are these constraints?
(Hint: these constraints lead to the major and minor symmetries of C)

The major and minor symmetries of the elasticity tensor, C, reduce the number of independent components from 81 to 21. How do we get from 21 components to less (e.g., some materials only need two components: Young’s modulus and Poisson’s ratio)?
The material itself imposes further constraints on C depending on its symmetries, further reducing the number of independent components.
What is an orthotropic material?
How many independent constants of the elasticity tensor, C, are needed to describe an orthotropic material?
An orthotropic material has three mutually orthogonal planes of symmetry (ex. wood).
You need 9 independent constants of C to describe an orthotropic material.
What is a cubic material?
How many independent constants of the elasticity tensor, C, are needed to describe a cubic material?
A cubic material has three mutually orthogonal planes of symmetry plus a 90° rotation symmetry with respect to those planes (ex. metals such as zinc, copper, aluminum, silver, and gold).
You need 3 independent constants of C to describe a cubic material.
What is an isotropic material?
How many independent constants of the elasticity tensor, C, are needed to describe an isotropic, linearly elastic material?
An isotropic material has physical properties that are identical in all directions (ex. glass).
You need 2 independent constants of C to describe an isotropic, linearly elastic material.
(These are the Lamé constants)
What is a monoclinic material?
How many independent constants of the elasticity tensor, C, are needed to describe a monoclinic material?
A monoclinic material has only one plane of symmetry (ex. gypsum, borax).
You need 13 independent constants of C to describe a monoclinic material.
What is an anisotropic material?
How many independent constants of the elasticity tensor, C, are needed to describe an anisotropic material?
An anisotropic material has no planes of symmetry (ex. quartz, wood, composites)
You need 21 independent constants of the elasticity tensor, C, to describe an anisotropic material.
What is the equation for stress in terms of strain and the Lamé constants?
These equations are also known as the constitutive equations