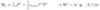Symmetry + Relativity Flashcards
To add: energy-momentum flow, stress tensor, spinors, wave-like equations
What is an “inertial” reference frame?
One n which N1 is obeyed - a particle subjeted to no forces does not accelerate
Postulate 1
‘Principle of Relativity’ The laws of physics are the same in all inertial frames of reference.
Postulate 2
The Constancy of Speed of Light in Vacuum The speed of light in vacuum has the same value c in all inertial frames of reference.
What is an ‘event’?
A point in spacetime
What is the worldline?
The line of events which give the location of the patcile as a function of time
What is the spacetime interval? What is a timelike interval (explain in words too)?
s^2 = -c^2(t2-t1)^2 + (x2-x1)^2 + …
s^2 negative
a particle can travel from one event to another
an nxm matrix has how many rows?
n rows m columns
What is the inverse of a 2x2 matrix (a b) (c d)
1/(ad-bc) *
(d -b)
(-c a)
Lorentz factor gamma
1/(1-(v/c)^2)^1/2
d/dv (gamma) =
gamma ^ 3 * v/c^2
dt/dtau =
gamma
d/dv (gamma*v) =
gamma^3
Lorentz Transformations (all)
ct’ = gamma (ct - bx)
x’ = gamma (-bt + x)
y’ = y
z’ = z
velocity addition (all) also do vector version
ux` = (ux - v)/(1-ux*v/c^2)
uy` = uy/gamma(1-ux*v/c^2)
u[parallel]’ = (u[pa] - v)/(1-u.v/c^2)
u[perp]` = u[pe]/gamma(1-u.v/c^2)
Lorentz transformation matrix
g -gb 0 0
-gb g 0 0
0 0 1 0
0 0 0 1
define rapidity p
tanh(p) = v/c = beta
cosh(p)
sinh(p)
exp(p)
lorentz matrix in p
g
bg
(1+b/1-b)^1/2
cosh(p) -sinh(p) 0 0
-sinh(p) cosh(p) 0 0
0 0 1 0
0 0 0 1
mathematically, what is a lorentz transform. How does this effect 4-vectors
a rotation in spacetime the length of a 4-vector is conserved between frames
define 4-velocity what is its vector form
U=dX/dtau = (gc, gu)
4-acceleration?
A = dU/dtau
= g dU/dt
= g (dg/dt * c, dg/dt * u +ga)
= g^2 (u.a/c * g^2 , u.a/c^2 * g^2 * u + a)
a is three acceleration
dg/dt =
g^3 * u.a/c^2
what is the relation between 4-acceleration and 4-velocity
they are always orthogonal
4-force F =
F = dP/dtau
= (g W/c, g f)
f is 3-force = dp/dt
W = dE/dt
4-momentum P =
P = m0U
= g m0 dX/dt
= (g m0 c, g mo u)
= (E/c, p)
Wave vector K =
K = (w/c, k)
4-Force F=
F = dP/dtau =
(g*W/c, g*f)
f = 3-force = dp/dt
what is the scalar product of 2 4-vectors
a Lorentz-invariant quantity
for a pure force W =
dE/dt = f.u
f[para]’ =
f[perp]’ =
(f[pa] - (v/c^2)*dE/dt)/(1-u.v/c^2)
f[pe]/g(1-u.v/c^2)
phase velocity vp =
vp = w/k
dro/dtau =
a0/c ao = proper acceleration
[1] [2]->v_21 [3]->v_32 find the rapidity of [3] in the frame of [1] (v_31)
p_31 = p_21 + p+32
To derive the Dopplar Effect
K.U
to derive the headlight effect or aberration
K = (LAMBDA)^-1 K_0
What is a pure force?
U.F=0
dm0/dtau = 0
dE/dt = f.u
particle moves with velocity u in S S’ is moving with velocity v wrt S what is gamma_u’ = gamma for particle in S’
gamma_u gamma_v (1-u.v/c^2)
how does the pressure change from frame to frame
it stays the same
for a pure force dg/dt =
f.v/mc^2
an instantaneous rest frame is
an inertial frame
constant proper acceleration leads to
hyperbolic motion
equation of a hyperbola
(x-b)^2 - (ct)^2 = (c^2 / a_0)^2
for constant proper acceleration tau =
c*ro/a_0 ro = rapidity
A.A =
a_0 ^2
zero component lemma
if one component of a 4-vector is zero in all reference frames, then the whole 4-vector is zero
what do the “Zero component lemma” and 4-momentum conservation imply
4-momentum conservation energy conservation
P.P =
-m^2 c^2
energy momentum invariant
E^2 - (pc)^2 = m^2 c^4
velocity in terms of momentum and energy
v = pc^2 / E
P = P_1 + P_2 how to eliminate P_2 ?
‘Isolate and Square’
P_2 = P - P_1
P_2 . P_2 = (P - P_1).(P - P_1)
= -(m_2 c)^2
what is an elastic collision in special relativity
one in which the rest masses do not change
for a photon relate energy and momentum
E = pc
what is []’phi what does this imply?
a lorentz-invariant scalar field
[]’phi = /\ [] phi
hence []phi is a 4-vector
[] =
-1/c * d/dt
d/dx
d/dy
d/dz
all partial
4-Divergence [].F =
[]^T g F = 1/c dF0/dt + nabla(f)
D’Alembertian []^2 =
[].[] = []^T g []
= -1/c^2 d^2/dt^2 +nabla^2
nabla^2 is the Laplacian
wave equation in terms of a scalar field
[]^2 phi = 0
[].X =
4
[].(K.X) = K is a constant 4-vector
K
p + p –> p + p + pion
p hits stationary p
how to find threshold energy of incident p for pion creation
compare LABF before and ZMF after
equate energy invariants threshold energy
=> particles are stationary in ZMF
electromagnetic force f =
q ( E + v ^ B )
transformation of electromagnetic field (parallel and perp)
E[pa]’ = E[pa]
E[pe]’ = ga (E[pe] + v^B)
B[pa]’ = B[pa]
B[pe]’ = ga (B[pe] -v^E/c^2)
electric field in a capacitor
charge per unit area / e0
J 4-vector
(pc, j) p is charge density j is current density
maxwell 1
div E = charge density/e0
maxwell 2
div B = 0
maxwell 3
curl E = -dB/dt
maxwell 4
curl B = mu0 j + mu0 e0 dE/dt
j is current density vector
B in terms of vector potential
B = curl A
E in terms of vector and scalar potential
E = - grad phi - dA/dt (partial)
quote the gauge transformations
A -> A + grad chi
phi -> phi - dchi/dt (partial)
grad(1/r)
-1/r^2 r[hat]
4-vector potential A and its gauge transformation
A = (phi/c , A)
A -> A + []chi
maxwell equations in 4-vector potential
[]^2 A = -1/(e0 c^2) J
with [].A=0
B in terms of E
B = v ^ E / c^2
Liénard-Wiechert Potential of an arbitrarily moving charged particle
A = q/(4 pi e0) * (U/c) / (-R.U)
A is 4 vector potential
U is 4 velocity of particle
R is 4 displacement from particle to point of interest (where we want to know the potential)
poisson equation
nabla^2 phi = -p/eo
p is charge density
for a 4-vector A A’ =
A’ = /\ A
M1 integral form
integral (E.dS) = Qenc / e0
integral over a gaussian surface = E * surface area
M3 integral form
int over closed curve (E.dl)
= -d/dt surface int (B.dS) open surface integral
M4 integral form
int over closed curve (B.dl) =
mu0 surface int (J.dS) + mu0 e0 d/dt surface int (E.dS)
both are open surface integrals
T’ =
T is a tensor
T’ is that tensor in a new frame
T’ = /\ T /\^T
what is a 0th rank tensor
a scalar invariant
what is a 1st rank tensor
a 4-vector
what is a 2nd rank tensor
something that transforms like T’ = /\ T /\^T
what is ab^T
eg:
(1, 2, 3)(10; 20; 30) =
an outer product = a 2nd rank tensor
=
(10, 20, 30;
20, 40, 60;
30, 60, 90)
T . B =
T is a tensor
B is a 4-vector
= T g B
g is the metric
index notation summation convention
(Tensor).(4-vector)
A^ab X_b =
SUM_(b=0 ->3) [A^ab X_b]
define the metric tensor
A^T g B = A’^T g’ B’
=> g’ = (/\^-1)^T g /\^-1
how does a contravariant 4-vector transform
(thing)’ = /\ (thing)
the kind of 4-vector we are used to
how does a covariant 4-vector transform
give an example
(thing)’ = (/\^-1)^T (thing)
gX
index lowering for 4-vectors
F_a =
hence A.B =
F_a = g_ab F^b
A.B = A^T g B
= A^a g_ab B^b
= A^a B_b
index raising for 4-vectors F^a =
F^a = g^ab F_b
where g^ab = (g_ab)^-1
define g^ab
what does this imply
g^ab g_ab = delta^a _b
delta is the kronecker delta
=> g^ab is the inverse of g_ab
partial
delta_a = []_a
delta^a = []^a
which is the normal []
d/(dx^a) = (1/c d/dt, d/dx, d/dy, d/dz)
delta^a = g^ab delta_b
= same as above but first term is negative
^a is the normal []
rules for tensor sum
same number of indices
same valence - number up and down
rules for tensor outer product
for 4-vectors, examples:
A^a B^b = T^ab
A^a B_b = T^a_b
A^a_b B^c_de = C^ac_bde
rules for tensor contraction
A^a B_b
F^ab
there must be one up and one down
examples
A^a B_b -> A^a B_a
F^ab -> g_ac F^cb = F_a^b -> F_a^a = a scalar
in matrix notation what are:
A^ab B_b
A^ba B_b
A.B
B_b A^ba = B.A
remember the dot implies the metric is present
what is T^a_a
to start, take T^ab and post-multiply by the metric
-a0b0 + a1b1 + a2b2 + a3b3 + a4b4
[] in index notation
delta^a
product rule
partial delta^a (U^b V^c) =
(delta^a U^b) V^c + U^b (delta^a V^c)
4-curl, what is the outcome?
[]^A =
a combination of 2 lorentz boosts leads to…
a lorentz boost AND a rotation
the rotation comes from the geometry of spacetime
an object moving in a circle anticlockwise will precess in what direction
clockwise
Faraday Tensor
(0, Ex/c, Ey/c, Ez/c)
(-Ex/c, 0, Bz, -By)
(-Ey/c, -Bz, 0, Bx)
(-Ez/c, By, -Bx, 0)
the faraday tensor is antisymmetric, what does this imply
delta_a delta_b F^ab = 0
=> delta_a J^a = 0
=> charge conservation
1/2 F^ab F_ab =
B^2 - E^2 /c == D (invariant)
4 angular momentum
L = XP^T - PX^T
L^ab = X^a P^b - X^b P^a
the centroid x_c =
SUM (x_i E_i)/E_tot
dual tensor F(tilde)_ab
with example F(tilde)_12
1/2 E_abcd F^cd
E is levi-civita tensor
= 1/2(E_1230 F^30 + E_1203 F^03)
= 1/2( -F^30 + F^03 )
g^ab g_bc =
kronecker delta^a_c = identity
levi civita tensor definition
E_abcd =
+1 for 0, 1, 2, 3 and even permutations
-1 for odd
0 if two the same
E_01cd=
0 0 0 0
0 0 0 0
0 0 0 1
0 0 -1 0
shortcut for dual of an antisymmetric tensor F
F =
0 ax ay az
- ax 0 bz -by
- ay -bz 0 bx
- az by -bx 0
a -> -b b -> a
delta_a x^b =
1 if a=b
0 if a/=b
so = delta^a_b
delta_a x_b =
1 if a=b but -1 for a=0
0 if a/=b so = metric = g_ab
delta_a (k^a x_a) =
for constant 4 vector k
k^a delta_a (x_a) =
k^a g_ab =
k_a
delta^a sin(k^a x_a) =
[delta^a(k^a x_a)] cos(k^a x_a) =
k^a cos(k^a x_a)
nabla^ 1/r
laplacian (1/r) = -4pi diracdelta^(3) (r)
shorthand for d(x)d(y)d(z) - there are 3 deltas
div( a exp[i(k.r-wt)] ) =
i k.a exp[i(k.r-wt)]
curl( a exp[i(k.r-wt)] ) =
i k^a exp[i(k.r-wt)]
relate
k, c, w
w = kc
|E0| =
c |B0|
the Lorenz gauge
[].A = 0
in electrostatics …
there are fixed charges and no currents
General form of a retarded spherical wave.
How is this different to an advanced wave?
What do these look like
f = g(t - r/c)/r
- -> +
advanced wave collapses in to centre, retarded is the opposite
What do the Liènard-Wiechert potentials imply?
A depends on U and R but not acceleration.
radiated power:
energy flux
given by the poynting vector
N = e0c2 E^B
Larmor’s formula
PL = 2/3 * q2/4πe0 * a2/c3
Pauli-Lubaski 4-vector
indices “see-saw” trick
A^a_b B^b
= A^ab B_b
what are polar an axial vectors?
polar change sign under parity transformation. These are normal vectors like x, p. Axial vectors (like L, B) do not change sign
(polar vector) ^ (polar vector) =
axial vector
Lagrangian
what is it a function of
L = T - V
L( {qi}, {dqi/dt}, t)
Euler Lagrange Equations
d/dt (partial dL/dqi[dot] ) = partial dL/dqi
canonical momentum p(tilde) =
partial dL/dqi[dot]
generalised force
partial dL/dqi
Hamiltonian
H( q, p~, t) = SUM( p~i qi(dot) ) - Lagrangian
the action
how does this relate to euler lagrange eqns?
path integral (Lagrangian dt)
the paths of min/max action satisfy euler lagrange equations
Hamilton’s canonical equations
dq/dt = dH/dp
dp/dt = - dH/dq
for all qi
and p is pi~
lagrangian of a freely moving particle
-mc2/gamma
particle hits stationary particle, they stick together. How to find mass of combined partcle and its velocity?
compare lab initial and ZMF after
look for E2-p2=m2
find combined mass M
energy conservation from lab initial to lab final
E = gamma M
find gamma
