Symmetry Flashcards
Space group
Space groups represent the various ways motifs (such as atoms in xtals) can be arranged in space in a homogeneous array.
Each motif is equivilant to every other motif in the pattern
230 possible combinations of symmetry operations and translation operations in space
- Based on 1 of the 14 Bravais lattices
- Isogonal w/ 1 of the 32 point groups
Point group
The 32 possible combinations of rotational symmetry operations - both proper and improper
Point indicates that the symmetry operations are fixed around an “unmoved” center axis
- 21 without a center of symmetry
- 11 with a center of symmetry
Identical to the 32 crystal classes that are assigned based on morphology
The translation-free “residue” of a family of possible isogonal space groups
Isogonal
The rotation and screw axes have the same rotational angle
ex: 60° in a six-fold rotation (6) of six-fold screw axis (61)
Crystallography
The study of the external form and internal atomic arrangement of crystalline solids and the principles that govern their growth, external shape, and internal structure.
Unit Cell
The smallest unit of structure (or pattern) that can be infinitely repeated to generate the entire structure
Maintains the diagnostic properties of the mineral
Lattice
An imaginary pattern of points (or nodes) in which every point/node has an environment that is identical to that of every other point/node in the pattern
No specific origin as it can be shifted parallel to itself
Law of Bravais
Faces are most likely to develop parallel to lattice planes that have a high density of lattice points
The larger the number of points/nodes, the more common the face
Steno’s Law of the constancy of interfacial angles
The angles between equivilant faces of crystals of the same substance, measured at the same T, are constant
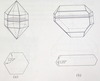
Symmetry Operations
The processes of rotation about an axis, of refection by a mirror, and of inversion about a central point
Rotation
Rotation is established by rotating a motif about an imaginary axis that intersects the crystal center
When rotational symmetry is present, a specific face on the crystal is repeated n times in a complete rotation of the crystal
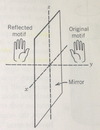
Reflection (mirror)
A mirror plane (m) is an imaginary plane that divides a crystal into two halves, each of which, in a perfectly developed crystal, is the mirror image of the other
A reflection across a mirror plane produces a mirror image
Inversion
A center of symmetry (i) is present in a crystal if an imaginary line can be passed from any point on its surface thru its center and the same point is found on the line at an equal distance beyond the center of the opposite side
Tested by confirming that for each face of the crystal there is some parallel face
Produces an enantiomorphic pair
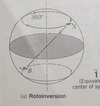
Rotoinversion
- First rotate the motif thru α (the rotation angle)
- Then invert the motif thru the center
Best seen and evaluated in 3D objects
Hermann-Maugin (HM) notation
The symbols for the overall symmetry content of a crystal
example:
i, 3A4, 4A3, 6A2, 9m
i = center of symmetry
3A4 = three four-fold rotations
4A3 = four three-fold rotations
6A2 = six two-fold rotations
9m = nine mirror planes
Miller Indices
The Miller indices of a face consist of a series of whole numbers that have been derived from the intercepts by inverting and, if necessary, the subsequent clearing of fractions.
Morphology
Morphology is commonly used to indicate the general outward appearance or shape of crystals
Crystal Habit
In crystallography, external shape is denoted by the term, habit whereas form is used in a special and restricted sense
Crystal Form
Crystal habit = external shape
Crystal Form is used in a special and restricted sense
A form consists of a group of like crystal faces, all of which have the same relation to the elements of symmetry
Translation
An ordered pattern can be generated by taking a motif and repeating it or translating it a specific distance t1
The external form of a crystal, although an expression of its internal structure, lacks any expresion of translation
Space Lattices
When the five planar nets are stacked in various ways along a third direction (z), periodic arrays in three-dimensions results
Primitive
A primitive space lattice is a parallelpiped with lattice points only at the corners
Nodes may be centered on a pair of opposite faces of the unit cell
When nodes are centered on a pair of opposite faces of the unit cell
A-centered = along the a (x) axial direction
B-centered = along the b (y) direction
C-centered = along the c (z) direction
F-centered
When nodes are centered on all faces of the unit cell
I-centered
When the node is present in the center of the unit cell, it is refered to as body-centered
Bravais Lattices
There are 14 lattices that are compatible with the 32 point groups
They represent the only possible wys in which nodes can be arranged in three dimensions
The varios lattices can be arranged among the seven crystal systems
Screw Operation
The combination of a rotarional operation with a translation (t) parallel to the axis of rotation
Any additional motifs are generated from the original motif in a 3-D, helical path - as in a screw motion
possible screws: 2, 21, 3, 31, 32, 4, 41, …
When the ratio of the subscript to the number of rotation is less than 1/2 the screw is right-handed
When the ratio of the subscript to the number of rotation is greater than 1/2 the screw is left-handed
Glide Operation
The combination of a mirror reflection with a translation component (t/2 or t/4) parallel to the mirror
also known as glide reflection
It relates motifs on either side of the line with a periodicity of hald the lattice translation
Glide Planes
3-D glide movements expressed in terms of the crystallographic axes: a, b, and c
Example: If it is parallel to the a-axis, then it is an a-glide. Similarly, if it is parallel to the b-axis, a b-glide, and a along the c-axis, a c-glide
diagonal (n) glides and diamond (d) glides exist
Right-handed
When the ratio of the subscript to the number of a rotation axis is less than 1/2
Defined as one that advances away from the observer when rotated clockwise
Left-handed
When the ratio of the subscript to the number of the rotation axis is greater than 1/2
Defined as one that advances toward the observer when rotated ?
R-centered
Contains lattice points at 1/3 and 2/3 along the body diagonal
