Superfluid 4He Flashcards
Viscosity
mass transport
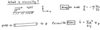
Lambda-transition
Plot heat capacity against Temperature for 4He. See phase transition at Tc. The plot looks like a lambda.
This new phase occurring at T<tc>
</tc>
Transport properties of the new liquid, He-II
The transport properties of this new liquid state are very strange. Here we consider three.
- Thermal conductivity (heat transport)
- Viscosity (mass transport)
- Fountain effect (coupled heat and mass transport).
Thermal Conductivity of He-II
Below Tc the boiling of the liquid ceases. This indicates that the liquid He-II has a very high thermal conductivity, unlike He-I. (Normal boiling in the body of a liquid results from hot spots, where the vapour pressure exceeds the saturated vapour pressure by more than the hydrostatic pressure in the liquid leading to the formation of a vapour bubble.
In He-II no such hot spots can occur, due to the large thermal conductivity, so that evaporation occurs entirely at the liquid-vapour interface) When the thermal conductivity was measured explicitly (take a narrow channel of 4 He with a heater at one end , measure the temperature difference between the ends as a function of Q) it was found that κ depended on the channel width and on the temperature difference. (Convince yourself this is not normal!)
Viscosity of He-II
The results of attempts to measure the viscosity depended dramatically on the method adopted: studies of flow of liquid or the drag on a moving object.
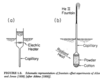
The fountain effect
In the fountain effect you have two regions of liquid separated by a very high flow impedance. If heat is applied to one side of the flow impedance, generating a temperature difference, then a flow of liquid occurs towards the hot side. In figure (a) below a new equilibrium is established with a pressure and temperature difference between the two regions. In figure (b) heat is converted into work producing a spectacular fountain of HeII. A temperature difference of 10-3K (1mK)can lead to a hydrostatic pressure differenceof order 10cm of 4 He (this depends on T)……so you can get a pretty high fountain!
Note that these effects are quite distinct from the convection that occurs in a normal fluid. Convection is inherently a dissipative process, here the flow is reversible and the state with a pressure a temperature difference shown in (a) is an equilibrium state. In convection, the flow of heat and mass are in the same direction, here they are opposite.
Fountain Pressure
(pressure for no net flow of liquid)
Modelling liquid 4He as an ideal gas
BEC for interacting bosons
On both experimental and theoretical grounds liquid 4 HeII has a BEC
BEC in dilute alkali gases
- extremely dilute clouds -> very low temps in nK range are required to observe BEC (seen in Rubidium, Li, Na)
- Atoms loaded into magnetic/optical trap. Cooled first by six orthogonal laser beams. Edge of trap manipulated to let energetic atoms escape. -> evaporative cooling through the BEC transition temp.
- Temperature characterised by velocity distribution (no thermal bath in usual sense), in classical case this is Max-Boltz vel dist.
- systems are dilute an weakly interacting (unlike 4He). Can choose atom to study both attractive (strongly inhibited when effectively att.) and repulsive interactions.
‘U-tube’ question.
Find PE of displaced levels, KE of flowing liquid, and angular freq.
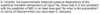
viscous penetration depth
δ = (2η/ωρ) 1/2
two fluid model (general)
This is a phenomenological macroscopic model proposed by Tisza in 1938, originally stimulated by the proposal of BEC in liquid helium. Starting from a limited number of assumptions a number of hydrodynamic equations are derived to describe the flow properties. These were able to provide a consistent description of many of the bizarre properties that had been observed. Importantly the model made explicit predictions of new phenomena that were subsequently observed experimentally, therefore providing corroboration of the validity of the theory. A microscopic interpretation of the theory was to follow, provided by Landau.
two fluid model (basis)
Heat flow
Poiseville flow
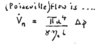
Thermal conductivity
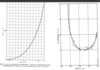
Andronikashvilii’s experiment
Normal density and viscosity as measured in Andronikashvilii’s experiment. Data is obtained from an analysis of the frequency and damping of the torsional oscillator.
Andronikashvilii’s experiment
Results (plots)
Results are shown below. Note that the temperature dependence of ρs is very different from that of BEC (not surprisingly).
Thermal counterflow.
Flow of superfluid and normal components in opposite directions (total fluid density remaining constant). Responsible for the anomalously high thermal conductivity of superfluid 4 He.
Second sound. A
temperature wave propagating through the fluid, predicted from the two fluid equations and first observed in Moscow by Peshkov.
dμ
and derivation of fountain pressure
dμ = -sdT +(1/ρ)dp
dμ = 0 thermodynamic equilibrium. But T1=/=T2 in fountain effect. This is possible because the mass is transferred via the superfluid component, which carries zero entropy.
-sΔT + (1/ρ)Δp = 0
Δp = ρsΔT
Flow of superfluid is driven by
gradient of chemical potential
normal fluids are accelerated by pressure gradients
In fountain effect, transfer of superfluid stops when mu1=mu2
Thermal equilibrium of two reservoirs of superfluid connected by a superleak
dispersion relation of elementary excitations in superfluid 4He
lowest energy excitations
phonons and rotons
Landau criterion for superfluidity
The form of the dispersion relation accounts for the fact that the fluid can flow with zero apparent viscosity up to some maximum critical velocity before the breakdown of superfluidity occurs. If the excitations were “particle like” as in BEC, this critical velocity would be zero.
phonon dispersion relation
ε = cp
roton dispersion relation
ε = Δ + (p - p0)2/2μ
where μ is mass not chemical potential here
landau formula for normal density
landau critical velocity
Determine that velocity for the Landau dispersion relation. What excitation is created? Show that for an ideal Bose gas the critical velocity is zero
Superfluid 4He - QM on macroscopic scale
in superfluid 4He - motion of condensate
quantisation of circulation
quantised vortices
vortex rings - critical velocities
