BEC Flashcards
Ideal Bose Gas

definition of quantum degeneracy

Condition for quantum degeneracy
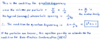
Why BEC? (Why do fermions not show this?)

What is BEC?

Distribution function for bosons

i) ‘particle in a box’ states
1. Find the single particle quantum states
Solve the SE for the eigenstates, find energies and wavefunctions

Derive energy density of states g(ε) for a free ideal gas

i) ‘particle in a box’ states
2. “counting” the states
no. of states with energy ε -> ε + dε
derive/use energy density of states to find g(ε)dε
Adding in ground state by hand to N
At T=0 all particles are in GS but g(ε) ∝ ε1/2, leaving GS zero contribution to mere integration of nbar(ε)g(ε)dε.
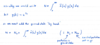
μ for macroscopic occupation of the ground state

i) ‘particle in a box’ states
3. Occupy the states
n(ε)d(ε) = no. of particles with energy ε -> ε + dε
how are particles distrubted over energy levels? Use B-E dist func nbar(ε) *g(ε)dε = n(ε)dε. Integrate for N.
Add in GS by hand.
mu for macroscopic population
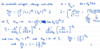
ii) ‘BEC in harmonic trap’


ii) BEC in harm trap


ii) BEC in harm trap

no. of quantum states is volume (no. of states) x f (degrees of freedom)

ii) BEC in harm trap


ii) BEC in harm trap


heat capacity (const volume)


Use expression for condensate fraction, rewrite for Nex, sub into internal energy estimate (N* the typ energy kT). Find Cv. Compare to classical C.

Evaluate internal energy
previously estimated. Now do integral!



