sorting algorithms

Question 1

Insertion sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 1

Insertion sort

1. any
2. O (n²)
3. O (n²)
4. O (1)
5. in place - yes
6. stable - yes

note - insertion sort is really fast for small arrays, even more than quick sort for example

Question 2

Bubble sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 2

Bubble sort

1. any
2. O (n²)
3. O (n²)
4. O (1)
5. in place - yes
6. stable - yes

Question 3

Merge sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 3

Merge sort

1. any
2. O (nlogn)
3. O (nlogn)
4. O (n)
5. in place - no
6. stable - yes

Question 4

Heap Sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 4

Heap Sort

1. any
2. O (nlogn)
3. O (nlogn)
4. O (1)
5. in place - yes
6. stable - no

Question 5

Quick sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 5

Quick sort

1. any
2. O (nlogn)
3. O (n²) - depends on pivot selection (generally the mean should be picked)
4. O (1)
5. in place - yes
6. stable - no

Question 6

Counting sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 6

counting sort

1. integers [0…k]
2. O (n+k)
3. O (n+k)
4. O (n+k)
5. in place - no
6. stable - yes

Question 7

Radix sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 7

Radix sort

1. integers with d digits in base b
2. O (d(n+b)) - assuming we use counting sort, for b = O (n) we will get O(n)
3. O (d(n+b)
4. depends on the used stable sort
5. in place - depends on the used stable sort
6. stable - yes

Question 8

Bucket sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 8

Bucket Sort

1. numbers with a unioform distribution from [0,1)
2. O(n)
3. O(n²)
4. O(n)
5. in place - no
6. stable - yes

Question 9

Selection sort

1. keys
2. average runtime
3. worst case run time
4. additional space
5. in place - yes/no
6. stable - yes/no

Answer 9

Selection sort

1. any
2. O(n²)
3. O(n²)
4. O(1)
5. in place - yes
6. stable - no (could be implemented as stable for added overhead)

Question 10

sort according to insertion sort

[50, 80, 10, 30, 90, 60]

Answer 10

Question 11

sort according to bubble sort

[9, 6, 2, 8, 3, 1, 7, 5, 4]

Answer 11

Question 12

sort according to merge sort

[7, 3, 2, 16, 24, 4, 11, 9]

Answer 12

Question 13

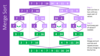
sort according to selection sort

[29, 72, 98, 13, 87, 66, 52, 51, 36]

Answer 13

Question 14

sort according to heap sort

[6, 5, 3, 1, 8, 7, 2, 4]

Answer 14

https://en.wikipedia.org/wiki/Heapsort#/media/File:Heapsort-example.gif

Question 15

sort according to quick sort (take 5 = pivot)

[8, 1, 6, 4, 0, 3, 9, 5]

Answer 15

[8, 1, 6, 4, 0, 3, 9, 5] (pivot = 5)

[1, 4, 0, 3, 5, 8, 6, 9] pivots = (3,6)

[1, 0, 3, 4, 5, 6, 8, 9] pivots = (1,8)

[0, 1, 3, 4, 5, 6, 8, 9]

Question 16

sort according to counting sort

[2, 3, 0, 5, 2, 3, 0, 0, 5] (k=5)

Answer 16

count the number of appearances of each number:

A [2, 3, 0, 5, 2, 3, 0, 0, 5]

0 1 2 3 4 5

C [3, 0, 2, 2, 0, 2]

go over C and find number of elements smaller than each number

C [3, 3, 5, 7, 7, 9]

go over A from end to beginning and place each number correct amount of times

[0,0,0,2,2,3,3,5,5]

Question 17

sort according to radix sort

329

457

657

839

436

720

Answer 17

sort each digit from right to left using a stable sort

329 720 720 329

457 436 329 436

657 457 436 457

839 657 839 657

436 329 457 720

720 839 657 839

Question 18

sort according to bucket sort

[0.87, 0.71, 0.36, 0.62, 0.27, 0.94, 0.12, 0.21, 0.32]

Answer 18

Creat array B

[, 0.12 , 0.27 , 0.36, , 0.62, 0.71 , 0.84, 0.94]

0.21 , 0.32

than sort each sub list using insertion sort and concat them