Data Structures Flashcards
(12 cards)
Heap
Adventages:
Build time:
Insert:
Get max:
Extract max:
Heap
Adventages: quick access to min/max. Can be used to implement priority queue. Heap sort
Build time: O (n)
Insert: O(logn)
Get max: O (1)
Extract max: O (logn)
stack
isEmpty:
Push:
Pop:
stack
isEmpty: O(1)
Push:O(1)
Pop:O(1)
queue
isEmpty:
enqueue:
dequeue:
queue
isEmpty: O(1)
enqueue: O(1)
dequeue: O(1)
Binary trees
full:
perfect:
complete:
pre/in/post order:
Binary trees

full: every inner vertex has exactly 2 children
perfect: a full tree where all leaves are the same depth
complete: obtained from a perfect tree by removing sequential leaves from the right.
pre/in/post order: root-left-right / left-root-right / left-right-root
Binary search Trees
search:
getMin/Max:
insert/remove:
select:
rank:
Binary search Trees
search: O(logn)
getMin/Max: O(logn)
insert/remove: O(logn)
select: given a tree and index i, return node x s.t x is the i’th element in size in the tree O(logn)
rank: given a tree and node x, return index i s.t x contains the i’th element in size in the tree O(logn)
Hash Tables
advantages:
Insert:
Search:
Delete:
simple uniform hashing -
Hash Tables
advantages: allows quick insert/search/delete operations
Insert: O(1) for simple uniform hashing
Search: O(1) for simple uniform hashing
Delete: O(1) for simple uniform hashing
assuming simple uniform hashing - meaning the table size is O(m), m~n, and the probability of each value to fall into any of the cells is uniform.
alpha = n/m is called the load factor and indicates the amount of values per cell.
Trie
advantages:
search:
Trie
advantages: used to manage a group of strings and allow quick information retrieval. can be used for autocomplete for example.
search : O(dm) where d is the size of the alphabet (generally constant) and m the hight of the trie, i.e the length of the longest word contained in it.
maximal number of edges for undirected graph:
maximal number of edges for directed graph:
maximal number of edges for undirected graph: n(n-1)/2
maximal number of edges for directed graph: n2
adjacency list
list[v] contains list of all of v’s neighbors
size:
is neighbor(u,v):
isEdge(u,v):
Allneighbors(u):
adjacency list
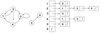
size: O(V+E)
is neighbor(u,v): O(deg u)
isEdge(u,v): O(deg u)
Allneighbors(u): O(deg u)
adjacency matrix
mat(i,j) = 1 if (i,j) in E, 0 otherwise
Size:
isNeighbor(u,v):
isEdge(u,v):
Allneighbors(u):
adjacency matrix
Size: O(V2)
isNeighbor(u,v): O(1)
isEdge(u,v): O(1)
Allneighbors(u): O(V)
weighted graph - description and representations
G= (V,E,W) is a graph where each edge has a weight associated with it.
it can be represented by an expanded adjacency list/matrix:
list: each edge in the list contains its weight
matrix: instead of containing binary values, the number in each cell contains the weight of the edge (or 0 if it doesnt exist, as before).
explain the data structure and implimintations
used for storing sets. has a make-set, find-set and union functions. can be implemented using a list (or hashmap) of linked-lists or as a list of trees. each item in the set contains a pointer to that set’s representative.


