Sorting Algorithms

Question 1

Is quicksort stable?

Answer 1

No

Question 2

Can quicksort be done in-place?

Answer 2

Yes

Question 3

Can merge sort be done in-place?

Answer 3

No. It requires O(n) space for the auxiliary array. There is an in-place version?

Question 4

Is merge sort stable?

Answer 4

Yes

Question 5

Is insertion sort stable?

Answer 5

Yes

Question 6

Can insertion sort be done in-place?

Answer 6

Yes.

Question 7

Can selection sort be done in-place?

Answer 7

Yes

Question 8

Is selection sort stable?

Answer 8

No

Question 9

Is heap sort stable?

Answer 9

No

Question 10

What’s the best-case running time of binary search?

Answer 10

O(1) - we get lucky and find the element right at the midpoint.

Question 11

What’s the worst-case running time of binary search?

Answer 11

O(log n)

Question 12

How to code selection sort? and time and cost?

Answer 12

O(n^2) time

O(1) space – in-place sort

Question 13

How to code insertion sort and cost?

Answer 13

Worst case: O(n^2) - everything in reverse/descending order

Best case: O(n) - everything in order/ascending

Question 14

Why is insertion sort quadratic O(n^2) when input is reverse order?

Answer 14

each time we insert an element into the sorted portion, we’ll need to swap it with each of the elements already in the sorted list to get it all the way to the start. That’s 1 swap the first time, 2 swaps the second time, 3 swaps the third time, and so on, up to n - 1n−1 swaps for the last item.

Question 15

Pseudo-code for merge sort

Answer 15

if len(list) < 2: return list

sorted_first = mergesort(first_half)

sorted_second = mergesort(second_half)

return merge(sorted_first, sorted_second)

Question 16

How to merge 2 sorted lists (during merge sort?)

Answer 16

Grab the smallest element from the 2 lists and append to auxiliary array

Question 17

What do you do when merging two sorted arrays and one of the two lists is already completed?

Answer 17

Copy over all the elements of the remaining list

Question 18

What is time complexity of merge sort?

Answer 18

O(NlogN)

Question 19

What is the base case to break out of merge sort recursion?

Answer 19

When the sublist only has 1 element (1 element list is already sorted)

Question 20

Merge sort visualized

Answer 20

Question 22

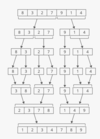
What can you do to preprocess a collection/list to make searching fasting?

Answer 22

Sort (e.g. binary search benefits from sorted list)

Question 23

What is the defintion of an in-place sort?

Answer 23

One that uses O(1) space

Question 24

What is the definition of a stable sort?

Answer 24

One where entries which ae equal appear in their original order

Question 25

What is the time complexity of python's sorted and sort method?

Answer 25

O(n logn)

Question 26

sorted(students) - in-place/mutate or returns new list?

Answer 26

Returns a new list new\_list = sorted(students)

Question 27

students.sort() mutates / in-place or returns new list?

Answer 27

In-place / mutates list

Question 29

How do you pass in a custom key to Python's sort built-in methods?

Answer 29

students.sort(key=lambda x: x.name) sorted\_students = sorted(students, key=lambda x: x.name)

Question 30

When pre-processing a collection/list by sorting first, what is the most likely best time complexity?

Answer 30

Depends on the sorting algorithm, but built-ins would be O(n logN)

Question 31

Quick sort time complexity average and best case?

Answer 31

O(N logN)

Question 32

Quick sort time complexity worst case?

Answer 32

O(n^2) when the input is already sorted

Question 34

Space complexity of quick sort?