Heaps Flashcards
What kind of binary tree is a heap?
Complete binary tree – every level (except possibly the last) is completely filled and all nodes are as far left as possible
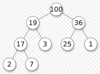
What is the heap property say about each node?
Each node is at least as great as th ekeys stored in its children

What are the indices of the children of a parent in an array representation of a heap?
2i + 1 and 2i + 2

What is the index of a child’s parent?
(i-1)//2

Time complexity of insertion in max-heap?
O(logN)
Why is the time complexity of an insertion in a max-heap O(logN)?
- Insert the new element at the bottom left-most node
- Then swim the new node up to maintain heap property
In the worst-case you have to swim all the way up which requires H compares where H is the height of the heap
Since heap is a complete binary tree and complete binary trees are balanced it has O(logN) height
Time complexity of lookup for max element
O(1)
Time complexity of deletion of max element in max-heap?
O(logN)
Why is deletion of max element in max-heap O(logN)?
Must swap max element with last element and then sink last element back down the height of tree (which has height of O(logN))
When should you use a heap?
- When all you care about is the largest or smallest elements (O(1))
- You do not need fast lookup, delete or search
What kind of heap does heapq.heapify([]) mutate in to?
min-heap
How can you use heapq.heapify([]) to create a max-heap?
Negate the priority/weight
ex:
heapq. heapify(arr)
heapq. heappush(arr, (-1, ‘value’))
What is the time complexity of heapq.heapify([])
O(n)


