Solid State Chemistry Flashcards
What is a solid?
A group of atoms interconnected by arrays of strong, directional chemical bonds. It’s as if they’re “super molecules.”
When this external mechanical force is applied to a solid, it will not flow.
stress
What is a crystal?
A solid whose structure is highly ordered and symmetrical over macroscopic distances
What is Haüy’s Law?
Stated by René-Just Haüy, when one cleaves a crystal, one will observe constant interfacial angles. Haüy concluded the outward symmetry implies a highly regular internal structure and the existence of a smallest crystal unit cell.
What is a symmetry element?
An potential action such as reflection or rotation that, if the new image is symmetric with the original, will perfectly superimpose that new image over the original image.
What is a crystal lattice?
A 3-D array of a network of all the points in a crystal in the same environment and of the same orientation
What is the cubic system?
A crystal lattice comprising cubic unit cells. It is the lattice of highest possible symmetry.
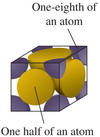
What is a unit cell?
The smallest space-filling body in volume that contains all structural information about its crystal
What is the shape of a unit cell in a crystal?
Parallelepiped
What are the cell constants?
The 3 edge lengths (a, b, c) and the 3 angles (α, β, γ) unique to each different kind of unit cell
What are the minimum essential symmetry and conditions on unit cell edges and angles for a hexagonal crystal system?
1X 6-fold rotation a=b, α=β=90°, γ=120°
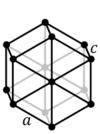
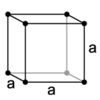
What are the minimum essential symmetry and conditions on unit cell edges and angles for a cubic crystal system?
4X independent 3-fold rotation axes (each 70.53° from each other) a=b=c, α=β=γ=90°
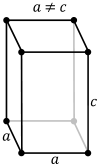
What are the minimum essential symmetry and conditions on unit cell edges and angles for a tetragonal crystal system?
1X 4-fold rotation a=b, α=β=γ=90°
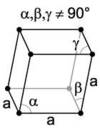
What are the minimum essential symmetry and conditions on edges and angles for a trigonal crystal system?
1X 3-fold rotation a=b=c, α=β=γ≠90°
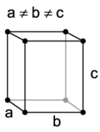
What are the minimum essential symmetry and conditions on unit cell edges and angles for an orthorhombic crystal system?
3X mutually perpendicular 2-fold rotations α=β=γ=90°
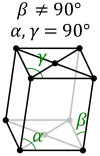
What are the minimum essential symmetry and conditions on unit cell edges and angles for a monoclinic crystal system?
1X 2-fold rotation α=γ=90°
What are the minimum essential symmetry and conditions on unit cell edges and angles for a triclinic crystal system?
None, None
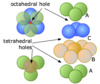
When would you use a nonprimitive unit cell over a primitive cell?
When the primitive cell lacks enough symmetry elements to be a unit cell
What are the 3 types of nonprimitive unit cells used to describe crystals?
1) body-centered
2) face-centered
3) side-centered
What is constructive interference?
When waves in phase encounter each other, reinforcing each other and thus amplifying the resulting wave. This occurs when the waves’ paths differ in length by a whole number of wavelengths. The amplitudes are additive.
What is destructive interference?
When waves out of phase encounter each other and combine to cancel each other out, producing a wave with an overall amplitude lesser than the originals’ average. The amplitudes are subtractive.
What is the Bragg law?
nλ = 2d sinθ
This law confirms if the waves in question are indeed diffracting on the crystal in question.
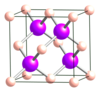
What is the simple cubic lattice?
The simplest form of crystal lattice in which the lattice points form perfect cubes with only 1 lattice point: 1 in the center. Po is the only element known to crystallize into a simple cubic lattice. Each unit cell contains 1 Po atom, separated from its neighboring Po atom by 3.35 Å.
What is the body-centered cubic (bcc) structure?
A cubic unit cell form with 2 lattice points: 1 in the center and 1/8 on each corner. All alkali metals crystallize into the bcc structure.
What is the face-centered cubic (fcc) structure?
A cubic unit cell form with 4 lattice points: 1/2 on each face and 1/8 on each corner. Al, Ni, Cu, and Ag crystallize into the fcc structure, among other metals.
How do you find the volume of a unit cell given its unit cell constants?
Cosine Law:
Vc = abc√[1-cos2(α) - cos2(β) - cos2(γ) + 2cos(α)cos(β)cos(γ)]
What is the lattice parameter?
The distance between the 2 nearest lattice points, often the value d from the Bragg law when n is a whole number.
Using the van der Waals equation of state for gas, how can we approximate the volume of a formula unit?
b/NA,
where b is the van der Waals paramter of the volume excluded per mole of gas
Using probability density functions of electron density, how can we approximate the volume of an atom?
V = 4/3 πr3,
where r is the radial distance from the nucleus at which the density function approaches a certain value.
Using X-ray (or some other suitable form of radiation) crystallography, how can we find the approximate volume of a formula unit?
V = 4/3 πr3,
where r is the radius of one formula unit and is found by halving the “nearest neighbor distance” between 2 nearest lattice points (tangent).
What is the nearest neighbor distance of a simple cubic?
a,
where a is the lattice parameter.
What is the nearest neighbor distance of a bcc?
(a√3)/2,
where a is the lattice parameter.
What is the nearest neighbor distance of a fcc?
(a√2)/2,
where a is the lattice parameter.
What is the packing fraction of a simple cubic?
π/6
What is the packing fraction of a bcc?
√(3π)/8
What is the packing fraction of a fcc?
√(2π)/6
What are the 2 ways of packing spheres?
Cubic close-pack (ccp) (AKA fcc) & Hexagonal close packing (hcp)
What is cubic close-packing (ccp), or fcc?
1 of 2 ways to most efficiently pack spheres together.
In ccp, the stacking pattern is abcabc…, and from a top view, no interstitial spaces are visible, though they exist.
What is hexagonal close-packing (hcp)?
1 of 2 ways to most efficiently pack spheres together.
Its stacking pattern is ababab…, and from a top view interstitial spaces are visible.
What is an interstitial site?
A center of free volume in a unit cell.
What are the 2 interstitial sites of a ccp, or interchangeably fcc?
Octahedral site & Tetrahedral site
What is a Bragg angle?
The angle from the crystal plane at which the incident radiation enters the crystal lattice matrix.
What is an octahedral site?
1 of 2 types of interstitial sites. It is surrounded at equal distances by 6 nearest-neighbor atoms. Octahedral sites lie at the midpoints of the edges of the fcc unit cell and at the center of the unit cell.
How many octahedral sites are there in total per fcc unit cell?
4
3 in total contributed from the edges (1/4 each, 12 points) & 1 at the center of the unit cell
How do you find the maximum radius of an interstitial atom at an octahedral site?
r2= a/2 - a√(2)/4
= 0.146a,
where
a = 2r2 + 2r1
and
r1 = a√(2)/4
What is a tetrahedral site?
1 of 2 types of interstitial sites. It is surrounded by 4 touching spheres. In fcc, it is in the volume between a corner atom and its 3 neighboring face-centered atoms.
How many tetrahedral sites are there in total per fcc unit cell?
8
What is the ratio of the octahedral-site radius to the host-atom radius?
r2/r1 = 0.414
What is the ratio of the tetrahedral-site radius to the host-atom radius?
r2/r1 = 0.225
What is an ionic crystal?
A solid compound formed by atoms with significantly different electronegativities. To a first approximation, these ions can be treated as hard, charged spheres (wave functions do not overlap) that occupy positions on the crystal lattice.
What elements typically react to form ionic crystals?
Groups I and II w/ Groups VI and VII (the great majority also crystallize in the cubic system).
Which compounds crystallize in the rock-salt (“sodium chloride”) structure?
The alkali halides (except cesium halides), ammonium halides, and alkaline-earth oxides and sulfides
What is the rock-salt structure?
An fcc lattice of anions whose octahedral sites are all occupied by cations, or vice versa. Each ion is surrounded by 6 equidistant ions of the opposite charge.
When is the rock-salt structure a stable crystal structure?
When the cation-anion radius ratio lies between 0.414 and 0.732 (assuming cations and anions behave as incompressible charged spheres, implying their wave functions do not overlap).
What is the cesium chloride structure?
An ionic crystal structure of 2 interpenetrating simple cubic lattices, 1 of anions and 1 of cations. This is achieved when the hard-sphere cation-anion radius ratio exceeds 0.732.
What is the zinc blende, or sphalerite, structure?
(Named after ZnS)
An ionic crystal structure consisting of an fcc lattice of S2- ions with Zn2+ ions occupying half of the available tetrahedral sites in alternation. This is achieved when the hard-sphere cation-anion radius ratio falls below 0.414.
What is the fluorite (CaF2) structure?
An ionic crystal structure based on an fcc lattice of Ca2+ ions. The F- ions occupy all 8 of the tetrahedral sites.
What is the significance of 0.414?
It is a ratio of octahedral-site radius to host-atom radius for an fcc lattice. When this ratio is exceeded (>0.414), the ion inserted into the octahedral site comes into contact with ions of the opposite sign in the rock-salt structure.
What is the significance of 0.732?
It is a ratio of tetrahedral-site radius to host-atom radius for a simple cubic structure.
Characterize the ionic bonds within ionic crystals, and discuss their macroscopic implications.
The strength and range of these electrostatic attractions make the respective crystals hard, high-melting, brittle solids that are electrical insulators.
Ionic solids are poor electrical conductors, so why are ionic liquids good electrical conductors?
Melting ionic solids breaks the strong electrostatic attractions, disrupting the lattice and setting the ions free to move.
Do metals have a tendency for ionic bonding? Why or why not?
Low tendency to form ionic bonding
Small differences in electronegativity
Do metals have a tendency for covalent bonding? Why or why not?
Low tendency for covalent bonding
Do not have nearly-filled subshells (to ease forming stable octet)
What is the Drude model of metal solid structure?
(Proposed by Paul Drude)
A fixed array of positively charged metal ions, each localized at a site of the crystal lattice. These fixed ions were surrounded by a sea of delocalized, mobile electrons, 1 from each of the atoms. It accounts for malleability, ductility, and conductivity.
Can a stable sodium molecule/cluster ever fill an antiboding MO in MO theory?
No
What is an energy band?
A collection of MO sublevels extremely close in energy (imagine forming a “bold font” MO line by bunching so many MO’s together)
The core AO electrons of Na retain their distinct, localized character of the ions at the lattice sites. Why?
The core AOs electrons of Na are only very slightly broadened at the equilibrium internuclear separation of the crystal
Most metals have crystal structures of high symmetry and crystallize in which lattices? Which metals have more complex crystal structures?
bcc, fcc, or hcp
Ga, In, Sn, Sb, Bi, & Hg
Metals can exist in crystal phase. Can metals also exist in liquid phase?
Yes.
In fact, the conductivity usually drops by only a small amount when the metal melts.
What provides the very strong binding in most metals?
The electron sea
This is manifested by their high boiling points, though they have a very large range of melting points.
What is a covalent (network) crystal?
A class of crystalline solids whose atoms are linked by covalent bonds. A classic example is diamond (cubic system). To bond, each hybrid orbital has at least 1 e- that can spin-pair with a corresponding e- from another, equivalent hybrid orbital.
These crystals have very high melting points and are hard and brittle.
What is a molecular crystal?
A group of molecules held in their lattice sites by intermolecular forces like hydrogen bond and van der Waals forces. Examples include noble gases, diatomics, some covalent molecules, metal halides of low ionicity (ex.: Al2Cl6, FeCl3, BiCl3), and most organic compounds.
How do you account for the complexity of attractive vs. repulsive forces in a molecular crystal from the large number of atoms?
1) Assume each atom is a sphere, with van der Waals radius, fused to each other.
2) Pack the spheres in such a way that no molecules overlap while minimizing empty space.
How do molecular crystals crystallize?
If simple geometry (ex: noble gas): highly symmetric fcc lattice.
If complex geometry: lowly symmetric monoclinic or triclinic system
Is it possible for an elemental ionic solid to exist?
Highly unlikely (pretty much “no”)
Characterize halogen solids.
Each halogen atom has 7 valence e- and can react with one more halogen atom. Once the single bond forms, the diatomic molecule can only interact with anoter diatomic molecule through van der Waals forces and form molecular solids with low melting points and boiling points.
Characterize chalcogen solids.
Structures vary.
O: can form 1 double or 2 singles. Highly prefers double bond (except O3), so forms weakly bound diatomics.
S: prefers 2 singles to 2 other S. Leads to (puckered) ring or chain structure. Ring is S8 (stable at room temp.). Above 160℃ rings break open and relink into long, tangled chains (viscous liquid). Weak intermolecular.
Se: prefers 2 singles to 2 other Se. Leads to ring or chain structure. Ring is Se8 (unstable). Stable form is very long spiral chains w/ weak interchain interaction (gray crystal, metallic appearance).
Te: similar to Se.
Characterize Group V elemental solids.
Similar trend to chalcogen solids.
N: prefers triples, forming diatomics.
P: 3 forms, each w/ 3 singles rather than 1 triple. White: tetrahedral P4 (weak van der Waals). Black and Red: bonded (in)directly with all other atoms in sample. Stronger.
As & Sb: Stable form like black P. Unstable form like white P.
Characterize metalloid solids.
Intermediate electronegativity, so exist as solids between metallic and covalent.
Sb: metallic luster, but poor conductor of electricity and heat
Si & Ge: semiconductors
Sn: 2 crystalline forms. White: tetragonal crystal structure, metallic conductor, stable above 13℃. Gray: powder, diamond structure, poor conductor (conversion: “tin disease,” prevented by small addition of Bi or Sb).
C: graphite is stable, not diamond. Graphite is sheets of fused hexagonal rings w/ weak interactions between layers, sp2 hybridization, remaining p is in extended π-bonding interactions over whole plane.
What is a semiconductor?
Intermediate conductor of electricity
What is an amorphous solid (glass)?
A crystal with so many defects that its crystalline order is destroyed. Otherwise resembles crystalline solid. Any substance that can be liquefied can almost certainly be prepared in an amorphous state by bypassing crystallization: cool molten material very fast.
Microscopically, strong tendency to form glass is associated w/ presence of ong/irregularly shaped molecules that can easily become tangled and disordered. Often used in fabrication into articles of any shape because the flow properties can be managed by controlling temp.
What are the 2 common point defects in a pure crystalline substance?
Vacancies (missing atoms)
Interstitials (added atoms)
What are Schottky defects?
Point defect in which a small fraction of the normal sites remain unoccupied.
Its concentration depends on temperature:
N = Nse-ΔG/RT,
where N is the number of lattice vacancies per unit volume,
- Ns* is the number of atom sites per unit volume
- ΔG* is the molar free energy of formation of vacancies
What are Frenkel defects?
Point defect in which atoms/ions are displaced (diffuse) from their regular lattice sites to interstitial sites. Prime examples are silver halides, where Ag+ occupies almost random sites.
Diffusion frequency depends on temperature:
D = D0e-ΔG/RT,
where D is self-diffusion coefficient.
Rates of diffusive motion vary enormously from one substance to another. In low-melting metals, very frequent. In high-melting metals, very rare.
What is a F-center (Farbenzentrum, or color center)?
Simplest of a family of electronic crystal defects, and imparts a color to ionic crystals.
In this defect, an uncharged atom attempting to diffuse to the surface of an ionic solid to escape encounters an anion vacancy and is trapped in the Coulomb field of the surrounding cations.
Explain the composition of nonstoichiometric compounds.
The solid compounds want to remain neutral, but the ion in question stably exists in multiple oxidation states, resulting in a varying composition of the ion and its ionic counterpart(s).
Examples include: FeO (wüstite) (2+/3+), NiO (2+/3+), Cu2S, TiO.
When NiO is prepared in 1:1 composition: pale green, electrical insulator. When prepared in excess of O2: black, conducts electricity well. Iin black, small fraction of Ni2+ replaced by Ni3+, so compensating vacancies occur at some Ni atom sites in crystal.
What is an alloy?
A mixture of elements that displays metallic properties. Related disorder to nonstoichiometric compounds (ionic).
2 types: substitutional & interstitial
What is a substitutional alloy?
Defect in which some of the metal atoms in a crystal lattice are replaced by other atoms (usually of comparable size).
Ex.: brass (Cu/Zn 33%) & pewter (Sn/Cu 7% / Bi 6% / Sb 2%)
What is an interstitial alloy?
Defect in which atoms of 1+ additional elements enter the interstitial sites of the host metal lattice.
Ex.: steel (mild: Fe/C 0.2%, high-carbon: Fe/C 1.5%)
What is an alloy steel?
Both substitutional and interstitial alloy: Fe/Cr (sub) / V (sub) / C (int)
What is lattice energy of a crystal?
The energy required to separate the crystal into its component atoms/molecules/ions at 0K.
How do you estimate the lattice energy of a molecular crystal?
Lennard-Jones potential
VLJ(R) = 4ϵ[(σ/R)12-(σ/R)6]
Vtot = 1/2 ∑i=1N∑j=1NVLJ(Rij),
where Rij is distance between atom i & atom j. When everything is calculated:
lattice energy = Vtot = 8.61ϵNA
This overestimates the true lattice energy because of zero-point energy (quantum).
Outline the Born-Haber cycle.
Applies Hess’s law to determine lattice energy of ionic crystal.
1) Convert ionic solid to elements in standard states (-ΔH°f).
2) Transform elements into gas-phase atoms (ΔH°f).
3) Transfer e- from potential cation to potential anion (IE & EA).
Assumes ΔU≈ΔH. Actually,
ΔH = ΔU + RTΔng,
where Δng is change in number of moles of gas molecules in each step of the reaction. Estimate overapproximates, presumably because short-range repulsive interactions & zero-point energy were not taken into account.
How do you estimate the lattice energy of an ionic crystal?
Coulomb’s Law
V = (q1q2) / (4πϵ0R0)
Vattraction = -e2/ 4πϵ0R0[2(1)+2(1/3)+2(1/5)+…]
Vrepulsion = e2 / 4πϵ0R0[2(1/2)+2(1/4)+2(1/6)+…]
Vnet = -NAe2 / 4πϵ0R0[2-(2/2)+(2/3)-(2/4)+…]
lattice energy = M(NAe2 / 4πϵ0R0),
where M is Madelung constant.
What is the Madelung constant? Give its value for different lattices.
The series in a 3-D version of Vnet approximation of lattice energy in an ionic crystal:
Vnet = -NAe2 / 4πϵ0R0[2-(2/2)+(2/3)-(2/4)+…]
Rock salt: M=1.7476
CsCl: M=1.7627
Zinc blende: 1.6381
Fluorite: 2.5194
