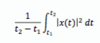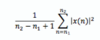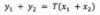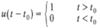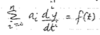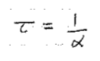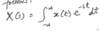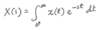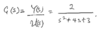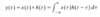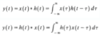Signals and Systems Flashcards
1
Q
What are samples?
A
Points of data
2
Q
What are sampling intervals?
A
The distance between the sample points
3
Q
Discrete-time signals can be defined in 2 ways…
A
- As a function
- As a list of values of a sequence
4
Q
In this picture, the arrow indicates….?
And if the arrow is not shown, where is the ____ point?
A
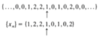
The n=0 point
The first value in the sequence is the n=0 point
5
Q
Define analog signals
A
Analog Signals: An analog signal is a continuous-time signal x(t) that can take on any value in the continuous interval (a, b), where a may be - ∞ and b may be +∞.
6
Q
Define Digital Signals
A
Digital Signals: A digital signal is a discrete-time signal x[n] that can only take on only a finite number of distinct values.
7
Q
What is a real signal?
A
Real Signals: A signal x(t) is said to be a real signal if its value is a real
number
8
Q
What is a complex signal?
A
Complex Signals: A signal x(t) is said to be a complex signal if its value is a complex number
9
Q
A general (continuous- or discrete-time) complex signal x(t) is a function of the form
A
where x1(t) and x2(t) are real signals and j = √−1
10
Q
Define Deterministic Signals
A
Deterministic Signals: Those signals whose values are exactly specified for any given time in the time span of interest are called deterministic signals. Such signals may be represented by a known function of time t.
11
Q
Define Random Signals
A
Random Signals: Those signals that take random values at any given time are called random or non-deterministic signals. Such signals must be characterized statistically (that is, represented in probabilistic terms)
12
Q
Any signal x(t) or x[n] can be expressed as a sum of ____ ____, one of which is ____ and one of which is ____
A
Any signal x(t) or x[n] can be expressed as a sum of two signals, one of which is even and one of which is odd
13
Q
The product of two even signals or of two odd signals is a…?
A
…even signal
14
Q
The product of an even signal and an odd signal is an…?
A
…odd signal
15
Q
Define Periodic continuous-time signals
A
Periodic Continuous-time Signals: A continuous-time signal x(t) is said to be a periodic signal with period T if there is a unique positive nonzero value of T for which the following expression is valid
16
Q
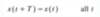
A dc signal is a signal in which x(t) is ____; such a signal is not periodic since its fundamental period is ____
A
A dc signal is a signal in which x(t) is constant; such a signal is not periodic since its fundamental period is undefined
17
Q
Define Aperiodic Continuous-time Signals
A
Aperiodic Continuous-time Signals: Any continuous-time signal which is not periodic is called a non-periodic signal or an aperiodic signal
18
Q
Define Periodic Discrete-time Signals
A
Periodic Discrete-time Signals: A sequence (discrete-time signal) x[n] is periodic with period N if there is a unique positive integer N for which the following expression is valid
19
Q
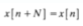
Define Aperiodic Discrete-time Signals
A
Aperiodic Discrete-time Signals: Any sequence which is not periodic is called a non-periodic sequence or an aperiodic sequence
20
Q
A sequence obtained by uniform sampling of a periodic continuous-time signal may…
A
…not be periodic
21
Q
The sum of two continuous-time periodic signals may…
A
… not be periodic
22
Q
The sum of two periodic sequences is…
A
…always periodic
23
Q
For any continuous-time signal x(t), the total energy of the signal over the interval t1 ≤ t ≤ t2 is defined as
A
24
Q
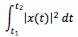
The average power of the signal x(t) over the interval t1 ≤ t ≤ t2 is defined as
A
25
|x(t)| denotes the ____ of x(t) and the signal x(t) could be a ____ or ____ signal.
|x(t)| denotes the **_magnitude_** of x(t) and the signal x(t) could be a **_real_** or **_complex_** signal.
26
For any discrete-time signal x[n], the total energy of the signal over the interval n1 ≤ n ≤ n2 is defined as
27
The average power of the signal x[n] over the interval n1 ≤ n ≤ n2 is defined as
28
A signal x(t) (or x[n]) is said to be an ____ \_\_\_\_ (or sequence) if and only if 0 \< E∞ \< ∞, in which case, P∞ = 0.
A signal x(t) (or x[n]) is said to be an **_energy_** **_signal_** (or sequence) if and only if 0 \< E∞ \< ∞, in which case, P∞ = 0.
29
A signal x(t) (or x[n]) is said to be a ____ signal (or sequence) if and only if 0 \< P∞ \< ∞, in which case, E∞ = ∞
A signal x(t) (or x[n]) is said to be a **_power_** signal (or sequence) if and only if 0 \< P∞ \< ∞, in which case, E∞ = ∞
30
A signal that does not satisfy 0 \< E∞ \< ∞ and 0 \< P∞ \< ∞ is not an ____ or a ____ signal
A signal that does not satisfy 0 \< E∞ \< ∞ and 0 \< P∞ \< ∞ is not an **_energy_** or a **_power_** signal
31
Define a **periodic signal**
A **periodic signal** is a power signal if its energy content per period is finite
32
If a \> 1, the time scaling operation is a ‘\_\_\_\_ \_\_’ process (it looks like a ‘\_\_\_\_’ process)
If a \> 1, the time scaling operation is a ‘**_speed_** **_up_**’ process (it looks like a ‘**_compression_**’ process)
33
If 0 \< a \< 1, the operation is a ‘\_\_\_\_ \_\_’ process (it looks like an ‘\_\_\_\_’ process
If 0 \< a \< 1, the operation is a ‘**_slow down_**’ process (it looks like an ‘**_expansion_**’ process
34
What would this sketch look like if it goes from x(t) to x(3t-5)?
35
Define a **system** (long)
A **SYSTEM** is a combination, collection or set of things or physical components connected or related together in such a manner to form a whole unit in order to achieve a certain task (or set of tasks) or objective(s). A system achieves its objective or set of objectives by transforming input signal(s) into output signal(s)
36
What is the **input** of a system?
An excitation or a stimulus that is applied to the system from an external source
37
What is the **output** of a system?
The actual response of the system due to the application of an input signal
38
What is a **system** (short)
A **system** can be considered a unit that transforms an input signal into an output signal using a well-defined rule or mathematical operation.
39
y = T(x) where T is the ____ \_\_\_\_ that maps _ onto \_
y = T(x) where T is the **_mathematical_** **_operation_** that maps **_x_** onto **_y_**
40
What does **SISO** systems stand for and what does it look like?
41
What does **MIMO system** stand for and what does it look like?
42
A system whose output at any time depends on only the input at that same time is called a...?
...memoryless system; otherwise, the system is said to have memory.
43
Example of a memoryless system?
A continuous-time signal
44
A discrete-time signal turns into a...?
...Continuous signal
45
What is a system with aid and memory?
A capacitor
46
System **with** memory are...
Systems **without** memory are...
...Dynamic
...Static
47
A causal system is one whose output 𝑦(𝑡) at time 𝑡 = 𝑡0 depends on only the inputs 𝑥(𝑡) for...?
...𝑡 ≤ 𝑡
48
If a system is not casual, it is a...?
...non-casual system
49
**All** **memoryless** **systems** are \_\_\_\_, but **not** **all** **causal** **systems** are \_\_\_\_
**All** **memoryless** **systems** are **_casual_**, but **not** **all** **causal** **systems** are **_memoryless_**
50
The system is a linear system if it satisfies the following two conditions...?
1. Superposition (or Additivity)
2. Homogeneity (or Scaling)
51
For the system to satisfy the superposition condition,
y1+y2 = ?
y1+y2 = T(x1+x2)
52
For the system 𝑦 = 𝑇(𝑥) to satisfy the homogeneity condition, it behaviour must satisfy...
𝛼∙𝑦 = 𝑇(𝛼∙𝑥)
53
A time-varying, or time-variant, system is one in which...?
...one or more of the parameters of the system vary as a function of time
54
Example of time-varying system
y = tx
55
A time-invariant system is one whose parameter(s)...?
...does not vary as a function of time
56
A time-invariant system: Mathematically...
𝑦 = 𝑇(𝑥)
57
A time-variant system: Mathematically
𝑦 = 𝑇(𝑥, 𝑡)
58
For time-invariant systems, a time-shift in the input signal leads to...
Although this is not true for...?
...the same time-shift in the output signal
...time-variant systems in general
59
1. A linear system that is also time-invariant is called a...
2. A nonlinear system that is time-invariant is called a...
3. A linear system that is not time-invariant is called a...
4. A nonlinear system that is not time-invariant is called a...
5. Static or dynamic systems can be ____ or ____ and can be \_\_\_\_- ____ or \_\_\_\_-\_\_\_\_
1. Linear Time - Invariant System
2. Nonlinear Time - Invariant System
3. Linear Time - Varying System
4. Nonlinear Time - Varying Systems.
5. Static or dynamic systems can be **_linear_** or **_nonlinear_** and can be **_time_**-_variant_ or **_time_**-**_invariant_**
60
In terms of impulse response, a system is ____ if its impulse response approaches ____ as time approaches \_\_\_\_
In terms of impulse response, a system is **_stable_** if its impulse response approaches **_zero_** as time approaches **_infinity_**
61
In terms of response to bounded input, a system is stable if...
...every bounded input produces a bounded output
62
Control systems can be classified into two general categories
1. Open-loop control systems
2. Closed-loop control system
63
A control system is a system whose function is to \_\_\_\_, \_\_\_\_, or ____ itself or another system
A control system is a system whose function is to **_command_**, **_direct_**, or **_regulate_** itself or another system
64
Define **open-loop control systems**
A control system whose input signal is independent of the output signal
65
# Define **closed-loop systems**
This class of systems are often called...?
A control system whose input signal is somehow dependent of the output signal
...**feedback control systems**
66
In a feedback system, the actual output signal of the system being controlled is...
...fed back and compared with the desired output signal to determine the appropriate control action or signal
67
If a system satisfies both superposition and homogeneity, it is \_\_\_\_, if neither then it's \_\_\_-\_\_\_\_
**_Linear_**, **_non-linear_**
68
If a system is linear, then x1+x2 → ? + ?
x1+x2 → x12+x22
69
What does LTI stand for?
**L**inear **T**ime **I**nvarient
70
LTI systems;
∂(t) = ?
x(t) = ? = ? x ? = ?
∂(t) = h(t)
x(t) = y(t) = x(t) x h(t) = ∞∫-∞ x(J) h(t-J)dT
71
When f(t) = 0 it's ?
If f(t) = u it's ?
Homogeneous
Non-homogeneous
72
Define **transient**
point of y(t) that dies down as t → ∞
73
Define **steady state**
point of y(t) that does **_not_** die down as t→∞
74
The degree of the differential equation is the one to the highest...?
power
75
In y(t) = est y(0)
s = ? for **Laplace**
s= ? for **Fourei**
**Laplace** s = ∂ + j*w*
**Fourei** s = j*w*
76
**BIBO** stands for...?
**B**ounded **I**nput **B**ounded **O**utput
77
x(t) = est
= est Y(gamma)
What is the **eigen function** and the **eigen value?**
est = **eigen function**
est Y(gamma) = **eigen value**
78
If it's constant it's ____ \_\_\_\_
If it's not constant it's ____ \_\_\_\_
**_Linearly dependant_**
**_Linearly independant_**
79
Method that can solve diff equations? (Involves D, r and y)
(D+r)y = 0
D = -r
y = CeDt
= Ce-rt
80
What is the discriminant and if it's \> 0 what does that mean?
b2 - 4ac \>0 means **real** and **distinct**
81
Both terms have to be less than 0 to be...?
...Stable
82
The unit step function \_\_, or the ____ step function, is a function with a value of 0 for ____ and _ for 𝑡 \> 0
The unit step function **_𝑢(𝑡)_**, or the **_Heaviside_** step function, is a function with a value of 0 for **_𝑡 \< 0_** and **_1_** for 𝑡 \> 0
83
The unit step function is ____ and may be represented mathematically as;
The unit step function is ____ and may be represented mathematically as;
84
Draw a Diagrammatic Representation of the unit step function
85
What is the Time Shift Operation on 𝑢(𝑡) mathematically?
86
Draw a diagrammatic representation of the **time shift operation**
87
Define the **unit impulse function**
The **unit impulse function** 𝛿(𝑡), or the **Dirac delta function**, is a **generalized function** on the **real number line** with a value of **0** **everywhere** **except** at **t = 0**
88
**The unit impulse function** has an ____ \_\_ _ over the entire real line
**The unit impulse function** has an **_integral of 1_** over the entire real line
89
The **unit impulse function** may be represented mathematically as:
90
Draw a Diagrammatic Representation of the **unit impulse function**
91
What does the Time Shift Operation on 𝛿(𝑡) look like mathematically?
92
It can be concluded that any continuous-time signal 𝑥(𝑡) can be expressed as,
x(t) = ∫...
93
The relationship between unit step and unit impulse functions can be expressed as
94
𝑒𝑗𝑞 =𝑒𝑗𝜔𝑡 = ?
𝑒𝑗𝑞 =𝑒𝑗𝜔𝑡=cos𝜔𝑡+𝑗sin𝜔𝑡
What is this known as?
95
𝑒𝑗𝑞 =𝑒𝑗𝜔𝑡=cos𝜔𝑡+𝑗sin𝜔𝑡
What is this known as?
The complex exponential signal
96
To summarize, a general complex exponential signal 𝑥 𝑡 = 𝑒𝑠𝑡 where s=𝜎+𝑗𝜔 can be written as:
𝑥 (𝑡) = 𝑒𝑠𝑡 =𝑒(𝜎+𝑗𝜔)𝑡 =𝑒𝜎𝑡(cos𝜔𝑡+𝑗sin𝜔𝑡)
97
𝑥1(𝑡) =𝑒𝜎𝑡 (cos𝜔𝑡) = ?
𝑥2(𝑡) =𝑒𝜎𝑡 (sin𝜔𝑡) = ?
𝑥1(𝑡) =𝑒𝜎𝑡 (cos𝜔𝑡) =𝑅𝑒[𝑥(𝑡)]
𝑥2(𝑡) =𝑒𝜎𝑡 (sin𝜔𝑡) =𝐼𝑚[𝑥(𝑡)]
98
1. If 𝜎 \< 0, it is a ____ sinusoidal function
2. If 𝜎 \> 0, it is an ____ sinusoidal function
3. If 𝜎 = 0 \_\_\_\_
1. If 𝜎 \< 0, it is a **_decreasing_** sinusoidal function
2. If 𝜎 \> 0, it is an **_increasing_** sinusoidal function
3. If 𝜎 = 0 **_constant_**
99
Equation for the **fundamental period**
100
Equation for the **fundamental frequency**
101
Equation for the **fudamental angular frequency**
102
**Linear differential equation** of the form:
is called a...?
...**homogeneous** **nth-order linear differential equation** if **f(t) = 0**; otherwise it is **non homogeneous**
103
dy/dt + ry = ? in terms of D
and so D = ?
And then this solution can be wirtten as;
y = ?
(D+r)y = 0
D = -r
y = CeDt
104
If D \<0, the response of the system naturally ____ as t...?
Therefore, the system is \_\_\_\_
If D \<0, the response of the system naturally **_decays_** as t...tends to infinity.
Therefore, the system is **_stable_**
105
If D\<0, the response of the system naturally ____ unboundelly as t...?
Therefore, the system is \_\_\_\_
If D\<0, the response of the system naturally **_increases_** unboundelly as t tends to infinity.
Therefore, the system is **_unstable_**
106
If the (b2-4ac) \> 0, the roots of the characteristic equation D1 and D2 are ____ and ____ (i.e. \_\_\_\_)
With the general solution being;
y = ? + ?
If the (b2-4ac) \> 0, the roots of the characteristic equation D1 and D2 are **_real_** and **_distinct_** (i.e. **_unequal_**)
With the general solution being;
y = **c1eD1t + c2eD2t**
107
If (b2-4ac) = 0 then the roots of the characteristic are ____ and \_\_\_\_
The general solution is
y = ? + ?
If (b2-4ac) = 0 then the roots of the characteristic are **_real_** and **_equal_**
The general solution is
y = **c1eD1t + c2**_t_**eD2t**
108
If (b2-4ac) \< 0 then the roots of the characterstic are ____ \_\_\_\_
The general solution is
y = ? + ?
If (b2-4ac) \< 0 then the roots of the characterstic are **_complex numbers_**
The general solution is
y = K1eD1t + K2eD2t
Using **Eulier's identity** the last expression can be simplified to
y = eøt(c1 cosßt + c2 sinßt)
Where c1 = K1 + K2
c2 = j(K1 - K2)
109
2nd-order systems have _ inital conditions, an nth-order system will have _ inital conditions
2nd-order systems have **_2_** inital conditions, an nth-order system will have **_n_** inital conditions
110
y''' - y' = 0
It's characteristic equation is...?
D3 - D = 0
111
Define **steady state response**
The point of the total response that **_does not_** approach **zero** as time approaches **infinity**
112
Define **transient response**
The point of the **total response** that approaches **zero** as time approaches **infinity**
113
y(t) = ya(t) + yb(t)
What is the **forced response** and what is the **free** **response**?
y(t) = ya(t) + yb(t)
ya is the **free response**
yb is the **forced response**
114
yb(t) = ∫ w(t-J)
What is w(t-J) called?
The **weighting function** or the **kernal** of the differential equation
115
wn = √(c/a)
What is this called?
The (undamped) **natural frequency** of the system
116
b/(2qw) = b/(2√(ac))
What is this called?
The **damping ratio** of the system
117
What is this called?
The **damping coefficient**
118
What is this called?
(The inverse of the damping coefficient) is called the **time-constant** of the system
119
This is provided in the data booklet, but what would the Laplace transform of a single-sided or unilateral look like?
Where would it be useful?
The change in ∞ to 0t
This would be particularly useful for finding the Laplace transform of functions that are **discontinuous** at t=0
120
In Laplace transform, L is called the...?
**Laplace transform operator**
121
What is Euler's Identity?
eajt = cos(at) + j sin(at)
122
**Time scaling:** If the Laplace transform of a function x(t) is x(s), then the Laplace transform of the function x(at) is given by...
L{x(at)] = 1/a . X(s/a)
123
**Division by t:** If the Laplace transform of a function x(t) is X(s), then the Laplace transform of x(t)/t is given by...
L{x(t)/t}= ∞∫s X(u)du
124
If you have an equation like this, what should you do?
1. Factorise
2. Partial fraction
125
The first term of on the right of the equation is the ____ \_\_\_\_ and the second term is the ____ \_\_\_\_ of the system
The first term of on the right of the equation is the **_forced response_** and the second term is the **_free response_** of the system
126
The **transfer function** of a LTI system is the point of the first term in the right side of the equation multiplying U(s)
127
Define the **transfer function** of a LTI system
The **ratio** of the Laplace transform of the **output variable Y(s)** to the Laplace transform of the **input variable U(s)**, with all initial conditions assumed to be **zero**
128
The output of any continuous-time LTI system is the...?
...convolution of the input with the impulse response of the system
129
What are the **roots** of the characteristic equation called?
**Poles**
130
What are the roots of numerator polynomial of the transfer function called?
**Zeros**
131
When is the system stable?
If **_all_** of the roots of the characteristic equation (that is the system poles) have negative real point/parts
132
The **transfer function**, G(s) = ?
G(s) = Y(s) / U(s)
133
What is the **characteristic equation** in this equation?
**Characteristic equation**: s2+4s+3
134
The characteristic equation is the...?
...denominator
135
What equation has very significant/ important mathematical implication?
𝑦(𝑡)=𝑇{𝑥(𝑡)} =𝑇{𝑒𝑠𝑡} =𝜆𝑒𝑠𝑡
136
In this equation 𝑦(𝑡) =𝜆𝑒𝑠𝑡
What is the **eigenvalue** and what is the **eigenfunction**?
𝜆 is the **eigenvalue**
𝑒𝑠𝑡 is the **eigenfunction**
137
y(0) = ?
𝑦 (0) = 𝜆 = 𝐻(𝑠)
138
Define **frequency response**
**Frequency response** is the **steady-state response** of a system to a **sinusoidal** **input** **signal**
139
What is 𝜙 and ∠?
𝜙 = ∠𝐺(𝑗𝜔)
∠ = tan-1
140
The magnitude and phase of the output signal differ from those of...
...the input signal
141
The output signal differ from the input signal only in...
...amplitude and phase angle
142
The amount of difference (in magnitude and phase) is a function of...
...the input frequency
143
The output signal and the signals throughout the system is...
...in steady-state
144
G (𝑗𝜔) is called the...
...**frequency response function,** it is also called the **sinusoidal transfer function**
145
The frequency response plot of a system is usually represented in two graphical plots...?
(i) the plot of 𝐺(𝑗𝜔) versus 𝜔
(ii) the plot of 𝜙(𝜔) versus ω
146
What is so special about a **bode** **magnitude** and **bode** **phase** plot?
The **frequency axis is a logarithmic scale**, these plots can be graphed over a **wide range of frequency**
147
Define **Bandwidth**
BANDWIDTH: The bandwidth of a system, 𝜔𝐵, is the frequency at which the magnitude of its frequency response function has declined by 3 dB from its low-frequency value. That is, the frequency 𝜔𝐵 at which
20𝑙𝑜𝑔 𝐺𝑗𝜔 =−3𝑑𝐵
148
Define **Gain Margin**
**GAIN MARGIN:** The gain margin of a system is the reciprocal of the magnitude of its frequency response function at the frequency at which the phase angle reaches −180°. That is,
𝐺𝑎𝑖𝑛 𝑀𝑎𝑟𝑔𝑖𝑛 = 1/ Magnitude of (𝐺 𝑗𝜔-180°)
149
Define **Phase margin**
**PHASE MARGIN:** The phase margin of a system is the difference between the phase angle at which the magnitude of its frequency response function is equal to unity and the −180° phase angle. That is,
𝑃h𝑎𝑠𝑒 𝑀𝑎𝑟𝑔𝑖𝑛 = 𝜙𝑃𝑀 = ∠𝐺 𝑗𝜔𝑐 − (−180°)
=∠𝐺𝑗𝜔𝑐 +180°
150
What is 𝜔c called and what does it do????
𝜔𝑐 denotes the frequency at which the magnitude of the frequency response function equals 1 and is called the gain crossover frequency
151
In a bode plot like this, where is the phase and gain margin?
152
The transfer function is G(s) = Y(s)/U(s) but what is it in terms of words?
Transfer function = Laplace transform of the output / Laplace Transorm of the input
## Footnote
Provided that all inital condinos are zero
153
Y = G.U What is G?
**The impulse response**
154
Frquency response is the _______ response and the _______ \_\_\_\_ and the \_\_\_\_\_\_\_\_\_\_
Frquency response is the **_function_** response and the **_phase_** **_angle_** and the **_frequency_**
155
# Define **Impulse response**
**Impulse Response:** The impulse response h(𝑡) of the continuous-time LTI system 𝑇 is defined as **the response of the system when the input is the unit impulse function 𝛿(𝑡)**. Mathematically, the impulse response can be represented as:
h(𝑡) =𝑇𝛿(𝑡)
156
Mathematically, how can the **impulse response** be represented?
Mathematically, the **impulse response** can be represented as:
h(𝑡) =𝑇𝛿(𝑡)
157
Any continuous-time signal 𝑥(𝑡) can be expressed as...
158
What is the equation known as the **convolution integral**?
159
y(t) = x(t)\*h(t) = ?
Whereas
y(t) = h(t)\*x(t)=?
160
Define the **step response**
**The step response 𝑠(𝑡)** of the continuous-time LTI system 𝑇 is defined as the **response of the system when the input is the unit step function 𝑢(𝑡).**
Mathematically, the step response can be represented as:
𝑠(𝑡) =𝑇 {𝑢(𝑡)}
161
How can **the step response** be represented mathematically?
Mathematically, **the step response** can be represented as:
𝑠(𝑡) =𝑇 {𝑢(𝑡)}
