Set Theory Flashcards
(63 cards)
1
Q
an unordered collection of distinct elements (items).
A
Set
2
Q
The two main ways to construct a set using symbols.
A
Roster and Set Builder
3
Q
Which type of set construction uses

A
Roster Notation
4
Q
Which type of set construction uses

A
Set Builder Notation
5
Q
“Such That” Symbol
A
(:)
6
Q

A
The set of everything
7
Q
The set of everything
A

8
Q

A
The set of nothing
9
Q
The set of nothing
A

10
Q

A
{1, 2, 3, 4, …}
11
Q

A
{0, 1, 2, 3, 4, …}
12
Q
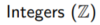
A
{…, −2, −1, 0, 1, 2, …}
13
Q

A
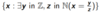
14
Q

A
The set of any positive, negative, or zero value
15
Q
{1, 2, 3, 4, …}
A

16
Q
{0, 1, 2, 3, 4, …}
A

17
Q
{…, −2, −1, 0, 1, 2, …}
A
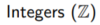
18
Q

A

19
Q
The set of any positive, negative, or zero value
A

20
Q

A
The compliment of set A
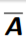
21
Q
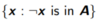
A
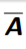
22
Q

A

23
Q

A

24
Q

A

25


26
The ___ of two sets (A and B) is the elements that are in A, but not B.
Difference (\)
27
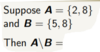
{2}
28
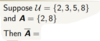
{3.5}
29
Assume A = {1, 2, 3}, B = {2, 4, 6}, C = {3, 4, 5}, and *U* = {1, 2, 3, 4, 5, 6}

{2,3,4,5}
30
Assume A = {1, 2, 3}, B = {2, 4, 6}, C = {3, 4, 5}, and *U* = {1, 2, 3, 4, 5, 6}
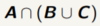
{2,3}
31
Assume A = {1, 2, 3}, B = {2, 4, 6}, C = {3, 4, 5}, and *U* = {1, 2, 3, 4, 5, 6}
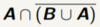
{}
32
Assume A = {1, 2, 3}, B = {2, 4, 6}, C = {3, 4, 5}, and *U* = {1, 2, 3, 4, 5, 6}
{1,2,4,5,6}
33

Element of / Membership / Containment
34
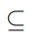
Subset of
35
Shorthand for
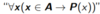
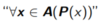
36
Shorthand for
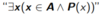
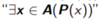
37
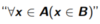

38

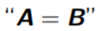
39
States that two sets are equal
Set Equality (=)
40
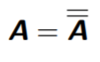
Double Negation
41
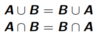
Commutative
42
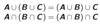
Associative
43
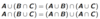
Distributive
44
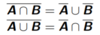
DeMorgan's
45
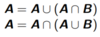
Absorption
46
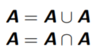
Idempotent
47
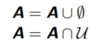
Identity
48

Inverse
49

Domination
50
The ___ of a set is the number of elements in it.
Cardinality
51
denoted using surrounding bars like those of the absolute value (||).
Cardinality
52
|{1,2,3}| =
3
53
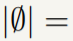
0
54


55
T or F. A set can contain itself.
False
56
T or F. A set can't contain itself.
True
57
The ___ of a set (A) is the set of all subsets of A.
Power Set
58
The cardinality of a Power Set is
2 to the cardinality of the original set.
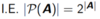
59
T or F. The power set of a set (A) contains A.
True
60
T or F. The power set of a set (A) doesn't contain A.
False
61

8
62

3
63

Cannot be determined


