Section 1.4

Question 1

How would you solve a Binomial approximation? E.g. (1-x/4)^10 1st 4 terms = 1-2.5x + 2.8125x^2 - 1.875x^3 Use expansion to estimate the value of 0.975^10 to 4 d.p.

Answer 1

1st) 0.975^10 = (1-x/4)^10 0.975 = 1-x/4 x/4 = 0.025 x = 0.1 2nd) Substitute in, (1-(0.1)/4)^10 = 0.7763

Question 2

In Binomial distribution, you can model X with B(n,p), if? (There are 4 aspects)

Answer 2

• there are a fixed number of trials, n - there are 2 possible outcomes (success and failure) - there is a fixed probability of success, p - the trials are independent of each other

Question 3

What does DRV stand for, and what is it?

Answer 3

DRV - discrete random variable Has a countable number of possible values, the probability of each value of a DRV is between 0 and 1, with the sum of all probabilities = 1

Question 4

What is discrete uniform distribution?

Answer 4

Symmetric probability distribution where a finite number of values are equally likely to be observed Every one of n values has equal probability of 1/n

Question 5

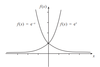
What are the graphs e^x and e^-x? Where do they cross the y-axis?

Answer 5

Intercepts at y = 1

Question 6

What is log_an = x equivalent to? (a not equal to 1)

Answer 6

n = a^x

Question 7

Laws of Logarithms:

Provide the formulas for:

• Multiplication Law
• Division Law
• Power Law

What happens when you have log_aa?

Answer 7

• Multiplication: log_ax + log_ay = log_axy
• Division: log_ax - log_ay = log_a(x/y)
• Power: log_a(x^k) = klog_ax

log_aa = 1, (a > 0, a not equal to 1)

Question 8

How would you solve 4(3^2x+1) + 17(3^x) - 7?

Answer 8

Make 3^x = y

Remember that 3^{2x + 1<em> </em>}= 3^2x x 3¹ = 3(3^2x)

So now, 4(3(y²)) + 17y - 7 = 0

= 12y² + 17y - 7 = 0

y = −17±√17^2−4x12x(-7) 2(12)

y = 1/3, y = -7/4

Then,

3^x = 1/3, log₃3^x = log₃1/3, x = log₃1/3, x = -1

3^x = -7/4, log₃3^x = log₃-7/4, x = log₃-7/4, x = no answer

So the answer is:

x = 1

Question 9

What is the graph y = Inx a reflection of, and in what line on the axes?

Answer 9

Reflection of graph y = e^x, in line y = x

Question 10

What does In x = in log form?

What does e^{In x} = ?

Answer 10

In x = log_ex

e^{In x} = In(e^x) = x

Question 11

The graph function g(x) = Ae^Bx + C has asymptote y =2, find C

Answer 11

As C is added to the function, the asymptote y = 2 represents C, as Ae^Bx will never be 0

So C = 2

Question 12

If y = axⁿ, then the graph of log y against log x, will the line be curved or straight, what will be its gradient, and what will be the vertical intercept (y-intercept)?

Answer 12

Straight Line

Gradient n

Vertical (y) intercept log a

Question 13

If y = ab^x then graph of log y against x, will it be a curved or straight line, what will be its gradient, and what will be its vertical (y) intercept?

Answer 13

Straight Line

Gradient = log b

Vertical (y) intercept = log a

Question 15

When a light inextensible string passes over a small pulley, what does it mean for the tension in both sides of the pulley if each end has a particle?

Answer 15

Tension in the string will be the same both sides

Question 16

When a particle on a pulley has a particle with a mass of 3m and accelerating at 1/3g, how would you find the tension in terms of m?

Answer 16

3mg - T = 3m x 1/3g = mg

2mg = T

Remember to always add g to such masses when used as a force

Question 17

When working with particles, what must you add to the mass in order to make it a force (in N) acting downwards?

E.g. 400g, show as a force

Answer 17

g = gravitational potential = 9.8

400g = 0.4gN

Question 18

Consider particles A and B on a pulley. When A hits the ground, the string slacks then becomes taut. What does B do, and how is it represented via t?

Answer 18

B reaches the max height t seconds after A hits the ground, then will take t seconds to return to its original position before it was taut.

Means that the time taken for this action

= 2t

Question 19

When given a question involving 2 particles, and have not been given the values for acceleration and Tension, how do you work out acceleration?

Answer 19

Form 2 simultaneous equations, 1 for each particle, in order to find acceleration

Question 20

How do you find the magnitude of the force exerted on the pulley by the string?

Why not use F from each particle?

Answer 20

Use the tension for the opposite and adjacent, then use Pythagoras to find the magnitude (hypotenuse)

Because those values of F are the forces exerted on the particle, not the pulley

Question 21

When integrating equations, what must always be remembered at the end of the new equation?

Answer 21

+ c

Question 22

What does an indefinite integral always produce, and what does a definite usually integral produce?

Answer 22

Indefinite = function

Definite = value (usually)

Question 23

For a car towing a trailer, car = mass 1200kg, trailer = mass 400kg, with driving force 3200N, and acceleration = 0.4ms^-2. Find the Resistance acting on the trailer.

Answer 23

1st, deal with it as one particle: Driving force - sum of mass x k (F = ma)

Resistance to whole motion will = 1600k

3200N - 1600k = 640

k = 1.6

Resistance of Trailer = 400 x 1.6 = 640N

ANSWER = 640N

Question 24

When asked how you modelled an answer to a question involving particles and an inextensible string/rope. If you have simply one rope e.g. between car and trailer, how would you explain that you modelled the question with this in mind?

Answer 24

State that you considered acceleration of the car will be the same for the trailer when connected via the inextensible string/rope

Question 25

What does inextensible mean?

Answer 25

Unable to be stretched or extended