Risk Management Applications of Options/Swaps- R37/38 Flashcards
(15 cards)
Understand the following Options Strategies:
- Covered Call
- Protective Put
- Bull Call Spread
- Bear Call Spread
- Butterfly Spread
- Collar
- Long Straddle
- Short Straddle
- Box Spread
-
Covered Call
- Sell call on owned asset. In return for premium, upside potential is foregone.
-
Protective Put
- Buy put on asset. If hedged asset declines, put increases in value. Loss limited to premium.
-
Bull Call Spread
- Buy low strike, sell higher strike call. Profit if stock goes up.
-
Bear Call Spread
- Short bull spread: buy high strike call, short low strike call
-
Butterfly Spread
- Long 2 calls (one low strike, one higher). Short two calls with medium exercise. Profits if price stays near price of written calls.
-
Collar
- Combo protective put & covered call. If premiums are equal, called a zero-cost collar.
-
Long Straddle
- Long a call & put with same strike/expiration. Bet on volatility.
-
Short Straddle
- Short a call/put at same strike/expiration. If price remains unchanged, keeps both premiums.
-
Box Spread
- Combo bull call spread and bear put spread on same asset. Payoff to combine bull call and bear put spreads, regardless of the value of underlying (risk free rate).
What is the pay-off (formula) for an interest rate call and interest rate put option?
An interest rate call can be purchased to protect the rate on future borrowing. It makes a payment to the owner when the reference rate (aka underlying) exceeds the strike rate. LIBOR is the usual reference rate. If rates rise, the call pays off (by reducing the effective loan rate).
payoff = (NP)max(0, LIBOR - strike rate)
Interest rate put (has a payoff when the reference rate is below a certain strike). If rates fall, the option pays off (used to maintain a return on an asset).
payoff = (NP)max(0, strike rate - LIBOR)
Calculate the payoffs for a series of interest rate oucomes when a floating rate loan is combined with:
- An interest rate cap
- An interest rate floor
- An interest rate collar
An interest rate cap is an agreement in which the cap seller agrees to make a payment to the cap buyer when the reference rate exceeds a predetermined level called the cap rate or cap strike.
An interest rate floor is an agreement in which the seller agrees to pay the buyer when the reference rate falls below a predetermined interest rate called the floor rate or floor strike.
payoff = NPmax(0, LIBORt-1 - strike ratet)
An interest rate collar is the combination of a long floor and a short cap. A bank can use a collar to protect floating rate assets from falling rates. As rates fall, the bank receives payments on the floor, offsetting the falling rates on the assets. They forego upside, and must make payments on the short call if rates increase. They can take the opposite position (short floor/long call) if needed as well.
Explain why and how a dealer delta hedges an option position, why delta changes, and how the dealer adjusts to maintain the delta hedge.
A dealer delta hedges an option by c_ombining the option position with a position in the underlying asset to form a portfolio_. Delta hedging means that the value of this portfolio does not change in reaction to changes in the price of the underlying (over a short period of time).
This is dynamically managed. Delta is the c_hange in the price of an option for a one-unit change in the price of the underlying security_.
Unfortunately:
- Delta is only an approximation, and is less accurate for larger changes in the stock price (chg S)
- Delta changes as market conditions change
- Delta changes over time (w or w/o any other changes)

Interpret the gamma of a delta-hedged portfolio and explain how gamma changes as in-the-money and out-of-the-money options move toward expiration.
Gamma is the change in the value of delta given a change in the value of the underlying stock.
gamma = (change in delta) / (change in S)
Delta at expiration is 1.0 if in-the-money and 0.0 if out-of-the-money.
Options deep in/out will approach 1/0 before expiration.
Demonstrate how an interest rate swap can be used to convert a floating-rate loan to a fixed-rate loan (and vice versa).
Plain vanilla interest rate swap: Company X agrees to pay Company Y a periodic fixed rate on a notional principal. Company Y agrees to pay Company X a periodic floating rate on the same NP.
Calculate and interpret the duration of an interest rate swap
Formula for duration of a pay-floating and pay-fixed counterparty:
Each counterparty in a swap is either:
- Long a fixed CF and short a floating CF
- Short a fixed CF and long a floating CF
- For fixed-rate instruments, duration will be higher, since the change in interest rates will change the PVs of the fixed CFs
- For floating-rate instruments, duration is close to zero because the future CFs vary with interest rates, and the PV is fairly stable with respect to changes in rates.
Dpay-floating = Dfixed - Dfloating > 0
Dpay-fixed = Dfloating - Dfixed < 0
Explain the effect of an interest rate swap on an entity’s cash flow risk.
Discuss market value risk.
Cash flow risk is a concern with floating-rate instruments. Since their cash flows are reset each period, their MVs are subject to only minor changes. E.g., the maximum duration of a floating rate instrument is the length of its reset period and its minimum duration is 0.
Market value risk is a concern with fixed-rate instruments. The cash flows to fixed-rate instruments are set at inception, so there is little uncertainty. However, the duration of the fixed is much greater than floating.
Determine the notional principal value needed on an interest rate swap to achieve a desired level of duration in a fixed-income portfolio.
*Calculate the dollar duration of the portfolio plus a swap position
*Calculate the notional principal
The dollar duration of the portfolio plus a swap position is calculated as:
Vp(MDT) - Vp(MDp) + NP(MDswap)
The PM selects a swap of a certain maturity which determines the modified duration of the swap, MDswap. He then selects the NP that will achieve the desired MDT.
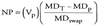
Explain how a company can generate savings by issuing a loan or bond in its own currency and using a currency swap to convert the obligation into another currency.
*List why a currency swap is different from an interest rate swap.
*Describe cash flows for a plain vanilla currency swap
- Two notional principals, and counterparties exchange them on the effective date and return them at the maturity date.
- Periodic interest payments are not netted-out, so each makes a payment in the appropriate currency.
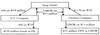
Demonstrate how a firm can use a currency swap to convert a series of foreign cash receipts into domestic cash receipts.
A series of foreign cash receipts can be combined with a currency swap with no notional principal payments to convert the receipts into domestic currency cash flows.
The foreign interest payments on the currency swap must equal the amounts of the foreign cash flows.
E.g, A US firm needs to convert quarterly fixed CFs of €1.25m into USD. The exchange rate is €0.833/$, and swap rates are 3.8% and 4%.
NP(0.04/4) = €1.25m
NP = €1.25m/ (0.04/4) = €125m.
USD = €125m / (0.833/1) = $150m
quarterly cash flows = $150m(0.038/4) = $1.425m
The swap would allow the firm to exchange its €1.25m quarterly inflo for $1.425m per period.
Explain how equity swaps can be used to diversify a concentrated equity portfolio, provide international diversification to a domestic portfolio, and alter portfolio allocations to stocks and bonds.
Concentrated portfolio: If you have 40% in one stock, you enter a swap to sell the total return of X% of that stock in return for that amount invested in a stock index.
International diversification: The firm trying to diversify its position could have a portfolio of stocks that is not the S&P 500. They will get a lower spread for an S&P 500 swap, which could introduce more risk (but is cheaper). There will be tracking error.
Basically, if you have Canadian stocks and want exposure to European stocks, you pay for a return based on the TSX and receive a return based on some Euro index.
Altering allocations: Just swap what you need - you can swap high-grade bonds for low-grade ones, but don’t confuse this for an interest rate swap (there is a capital gain component too)

What is an interest rate swaption?
What is the difference between a payer and receiver swaption?
An interest rate swaption gives the buyer an option to choose whether the swap will go into effect on some future date.
A payer swaption gives the buyer the right to be the fixed-rate payer (and floating-rate receiver) in a pre-specified swap at a pre-specified date.
A receiver swaption gives the buyer the right to be the fixed-rate receiver (and floating-rate payer) at some future date.
Demonstrate the use of an interest rate swaption to change the payment pattern of an anticipated future loan.
A corporate manager may wish to purchase a fixed-rate payer swaption to synthetically “lock in” a maximum fixed rate to be paid on an FRN to be issued in the future.
The manager enter into a swaption by paying a premium (today). The option expires at the time the loan will be taken out.
The payer swaption would convert a future floating-rate loan to a fixed-rate loan.
The receiver swaption would convert a future fixed-rate loan to a floating rate loan.

Demonstrate the use of an interest rate swaption to terminate a swap.
A manager who is under an existing swap can enter into a swaption with the exact characteristics of the existing swap, but take the other counterparty’s position. This cancels the existing swap with the swaption.



