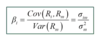Risk and Return

Question 1

Ways to measure Inflation

Answer 1

• CPI => Consumer Price Index, which measures the Purchasing Power of an average Citizen in the corresponding country
• The annual change in % of the CPI is called the Inflation

The nominal rate of return = real rate of return * expected Inflation

Question 2

The Real Interest Rate

Question 3

Equity Risk Premium (ERP)

Answer 3

• Average return of common stocks in the last 120 years: 11,5%
• Return of treasury bills (no risk alternative): 3,8%
• ERP = 11,5% - 3,8%= 7,7%
• It’s the premium, that can be earned by a long term investment in the stock market
• It’s earned by the willingness to take on stock market’s risks
• The EPR dependents on the historical data and the chosen time frame

Question 4

Drivers of the ERP in different Countries

Answer 4

• Higher Risk in some countries (Italy)
• Higher Inflation in some countries
• Ex-Post some countries might have been more fortunate than been expected
• Valuation levels increases, based on dividend yield or M/B-ratio => Optimism => lower risk premium in the future

Question 5

Measuring Risk, the Standart Deviation

Answer 5

• There is a difference between the expectation and the actual realization in any given year
• The return vary very much about the average over the last 100 years
• We can measure this spread with the standard deviation or the variance

Question 6

how to calculate the variance a standard deviation of stocks

Answer 6

Variance:

Variance = 1/(n-1) Σ (r_mt - r_m)²

standart deviation is the square root of the variance

the bigger the variance, the higher the risk

Question 7

reducing risk through diversification

Answer 7

• the higher the diversification, the lower the standard deviation
• that’s because a some events are good for one company and bad for another, if you own both companies, the effects will smooth each other out

Question 8

specific risk vs market risks

Answer 8

specific risks:

• the risk one events not benefitting the company => can be solved with diversification

market risk:

• you cannot get rid of this, because it will affect all companies

Question 9

Correlation Measures of different stocks

Answer 9

• Covariance:

measures how 2 variables change together

covariance > 0 they move together

covariance < 0 move in opposite ways

covariance = 1/(n-1) Σ (r_mt1 - r_m1)*(r_mt2 - r_m1)

• Correlation coefficient

It is similar to the Covariance, but it only moves between 1 and -1

Correlation coefficient = covariance / ( SD₁ * SD₂)

Question 10

calculating the risks and return of a portfolio

Answer 10

Expected return:

the weighted average of the expected return of all individual stocks

Portfolio risk:

Question 11

the variance of portfolios with equal parts of all stocks

Answer 11

variance =

1/N*average variance_stocks + (1-1/N)* average covariance

the bigger N gets the variance of the Portfolio becomes the average of the covariance, because the first part of the term gets close to zero, while the second multiplication becomes 1

Question 12

beta

Answer 12

• because a perfect diversified portfolio doesn’t have any specific risk only systematic or market risk.
• beta is the measurement of how stocks react to market risks
• beta=1 => the stock acts always similar to the market
• beta>>1 => the stock is very sensitive to the market, therefore you are getting a higher market risk
• beta is the slope of a regression model defined as: