Portfolio Theory and CAPM

Question 1

distribution of return

Answer 1

• short-run: the return distribution is close to normally-distributed
• long-run: the returns are log-normally distributed, because gains greater than 100% are possible, while losses bigger than 100% aren’t.
• convenient: normal distributions can be described with only two values, mean and variance

Question 2

basic intuition of portfolio theory

Answer 2

• combine various assets in portfolios that offer the highest possible returns for any given level of risk
• the investor identifies his/her risk appetite and the a portfolio will secure the highest expected returns => efficient portfolios

Question 3

construction portfolios in a return - standard deviation framework

Answer 3

• through creating a portfolio, we can have a higher return for any given risk
• this red line is called optimal frontier

Question 4

adding borrowing and lending into our model

Answer 4

• it’s possible to leverage and deleverage our portfolios now. that means we can change the risk and the return of every portfolio
• the red line is called tanget line

Deleverage:

asset 1: 5% expected return, 0% standard deviation => risk free

asset 2: 15% expected return, 16% standard deviation

portfolio_dl: 50% asset 1, 50% asset 2

expected return: 0,5*5%+0,5*15%=10%

expected risk: 0,5*0%+0,5*16%=8% => because asset 1 is riskfree, the will be no covariance

Leverage:

PortfolioL: 200% asset 2

expected return: 2*15% - 1*5% = 25%

expected risk: 2*16 = 32%

Question 5

The Sharpe Ratio

Answer 5

• Because we can lend and borrow money, the optimal portfolio will always be on the steepest feasible line.
• This optimal portfolio maximizes the ratio of risk premium to standard deviation
• this ratio is called “Sharpe Ratio” and is an important performance index (formula in the pic)
• an investment decision has 2 steps
  
  • 1.: finding the optimal Portfolio
  • 2.: deciding based on your risk appetite if you want to lend or borrow money => “Tobin Separation Theorem”

Question 6

Security Market Line

Answer 6

• shows the relationship between risk and return
• change the y-aches to beta instead of standard deviation and the tangent line is called SML
• beta is used instead of the SD because the perfect portfolio has no specific risk, only market risk.
• because you can (de)leverage this optimal portfolio and therefor (lower) higher the beta, beta determines your expected return

Question 7

The Capital Asset Pricing Model (CAPM)

Answer 7

• Based on the SML, we know that beta is the indicator of the expected return
• CAPM model the relationship between the expected return and the market risk
• The last part of the term is the market-risk-premium

Question 8

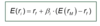
The implication of the CAPM

Answer 8

• Stocks above the SML are overperformers, they have a higher return for their risk than the market. Therefore they are very popular and everybody wants to buy them, nobody wants to sell => prices go up =>future return decreases and the stocks move back to the SML
• stocks under the SML are underperformers =>everybody wants to sell, nobody wants to buy => prices deceases => future return increases => move on the SML again
• stocks with a beta < 1 is a defensive stock
• stocks with a beta > 1 is an aggressive stock

Question 9

calculate beta

Answer 9

• Because the expected return isn’t measurable, we have to use data from the past, we get a testable version of the CAPM:
• Just transform the formula and calculate beta, formula looks like this:

Question 10

adjusting beta

Answer 10

• the past betas of big companies are often a good indicator for future betas, because they are (often) quite stable over time
• but there is a trend

beta < 1 implies a higher beta in the future

beta > 1 implies a smaller beta in the future

• Adjustment: future beta = 1/3 + 2/3*old beta
• Explaination:
• Managers decide to hold risk levels close to the market, so they lower or higher the betas
• low beta means low risk => cheaper capital cost => more investments => more risk => beta increases
• vice versa for bigger betas
• measurement errors

Question 11

empirical test CAPM

Answer 11

• Categorize all stocks by their betas and build 10 different portfolios with them, 1. portfolio has the 10% lowest beta, the 10. portfolio the 10% highest betas
• Analyzing multiple years 81931-1965) with rebalancing, there found a correlation between betas and the return => CAPM was proven
• they also analyzed 1966-2014 and found that there is no proof for the beta anymore => portfolio 8,9,10 performed worse than the ones with a lower beta

Question 12

Aarket Anomalies

Answer 12

• There is a correlation between market cap and return
  
  • the smaller the company, the bigger the return
• Good B/M value
  
  • when companies have a solid book value but the market does not value them => probably good returns

Question 13

Why is there contradicting evidence to the CAPM?

Answer 13

• Assumptions of the CAPM
  
  • the only relevant risk is market risk => beta is the only measure for risk
  • unlimited lending and borrowing is possible
  • investors try to maximize utility in a single period
  • investors have homogenous expectations
  • all assets are infinitely divisible
  • all information is available to all and free of charge
  • no taxes, transaction cost, market frictions

Question 14

Arbitrage Pricing Theory and other factor models

Answer 14

• assumes that stocks return depend on various factors with different sensitivity to these factors (factor loading)
• steps to get such a model

1. identify the factors
2. estimate the risk premium for these factors
3. estimate the factor leading of the individual stocks

Question 15

Multi-Factor-Models

Fama and French;

four-factor model of Carhart

Answer 15

Fama/French

• three Factors: size, value, and beta (market risk), see pic

four-factor model

• includes one more factor: Momentum