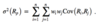Reading 9 - Probability Concepts: Learning Outcomes

Question 1

Random variable

Answer 1

A random variable is a quantity whose outcome is uncertain.

Question 2

Probability

Answer 2

Probability is a number between 0 and 1 that describes the chance that a stated event will occur.

Question 3

Event

Answer 3

An event is a specified set of outcomes of a random variable.

Question 4

Mutually exclusive events & Exhaustive events

Answer 4

Mutually exclusive events can occur only one at a time. Exhaustive events cover or contain all possible outcomes.

Question 5

Two defining properties of a probability

Answer 5

The two defining properties of a probability are, first, that 0 ≤ P(E) ≤ 1 (where P(E) denotes the probability of an event E), and second, that the sum of the probabilities of any set of mutually exclusive and exhaustive events equals 1.

Question 6

Empirical probability, subjective probability, and priori probability

Answer 6

A probability estimated from data as a relative frequency of occurrence is an empirical probability. A probability drawing on personal or subjective judgment is a subjective probability. A probability obtained based on logical analysis is an a priori probability.

Question 7

Probability of an event

Answer 7

A probability of an event E, P(E), can be stated as odds for E = P(E)/[1 − P(E)] or odds against E = [1 − P(E)]/P(E).

Question 8

Dutch book theorem

Answer 8

Probabilities that are inconsistent create profit opportunities, according to the Dutch Book Theorem.

Question 9

Unconditional probability

Answer 9

A probability of an event not conditioned on another event is an unconditional probability. The unconditional probability of an event A is denoted P(A). Unconditional probabilities are also called marginal probabilities.

Question 10

Conditional probability

Answer 10

A probability of an event given (conditioned on) another event is a conditional probability. The probability of an event A given an event B is denoted P(A | B).

Question 11

Probability of both A and B occurring

Answer 11

The probability of both A and B occurring is the joint probability of A and B, denoted P(AB).

Question 12

Probability of A given B

Answer 12

P(A | B) = P(AB)/P(B), P(B) ≠ 0.

Question 13

Multiplication rule for probabilities

Answer 13

The multiplication rule for probabilities is P(AB) = P(A | B)P(B).

Question 14

Probability that A or B occurs

Answer 14

The probability that A or B occurs, or both occur, is denoted by P(A or B).

Question 15

Addition rule for probabilities

Answer 15

The addition rule for probabilities is P(A or B) = P(A) + P(B) − P(AB).

Question 16

Independent vs. dependent events

Answer 16

When events are independent, the occurrence of one event does not affect the probability of occurrence of the other event. Otherwise, the events are dependent.

Question 17

Multiplication rule for independent events

Answer 17

The multiplication rule for independent events states that if A and B are independent events, P(AB) = P(A)P(B). The rule generalizes in similar fashion to more than two events.

Question 18

Total probability rule

Answer 18

According to the total probability rule, if S₁, S₂, …, S_n* are mutually exclusive and exhaustive scenarios or events, then *P*(*A*) = *P*(*A* | *S*₁)*P*(*S*₁) + *P*(*A* | *S*₂)*P*(*S*₂) + … + *P*(*A* | *S_n)P(S**_n).

Question 19

Expected value of a random variable

Answer 19

The expected value of a random variable is a probability-weighted average of the possible outcomes of the random variable. For a random variable X, the expected value of X is denoted E(X).

Question 20

Total probability role for expected value

Answer 20

The total probability rule for expected value states that E(X) = E(X | S₁)P(S₁) + E(X | S₂)P(S₂) + … + E(X | S_n*)*P*(*S_n), where S₁, S₂, …, S**_n are mutually exclusive and exhaustive scenarios or events.

Question 21

Variance of a random variable

Answer 21

The variance of a random variable is the expected value (the probability-weighted average) of squared deviations from the random variable’s expected value E(X): σ²(X) = E{[X − E(X)]²}, where σ²(X) stands for the variance of X.

Question 22

Variance

Answer 22

Variance is a measure of dispersion about the mean. Increasing variance indicates increasing dispersion. Variance is measured in squared units of the original variable.

Question 23

Standard deviation

Answer 23

Standard deviation is the positive square root of variance. Standard deviation measures dispersion (as does variance), but it is measured in the same units as the variable.

Question 24

Covariance

Answer 24

Covariance is a measure of the co-movement between random variables.

Question 25

**Covariance between two random variables**

Answer 25

The covariance between two random variables *R**_i* and *R**_j* is the expected value of the cross-product of the deviations of the two random variables from their respective means: Cov(*R**_i*,*R**_j*) = *E*{[*R**_i* − *E*(*R**_i*)][*R**_j* − *E*(*R**_j*)]}. The covariance of a random variable with itself is its own variance.

Question 26

**Correlation**

Answer 26

Correlation is a number between −1 and +1 that measures the co-movement (linear association) between two random variables: ρ(*R**_i*,*R**_j*) = Cov(*R**_i*,*R**_j*)/[σ(*R**_i*) σ(*R**_j*)].

Question 27

**Variance of return**

Answer 27

To calculate the variance of return on a portfolio of *n* assets, the inputs needed are the *n* expected returns on the individual assets, *n* variances of return on the individual assets, and *n*(*n* − 1)/2 distinct covariances.

Question 28

**Portfolio variance of return**

Answer 28

Question 29

**Calculation of covariance in a forward-looking sense**

Answer 29

The calculation of covariance in a forward-looking sense requires the specification of a joint probability function, which gives the probability of joint occurrences of values of the two random variables.

Question 30

**When two random variables are independent, the joint probability function is:**

Answer 30

When two random variables are independent, the joint probability function is the product of the individual probability functions of the random variables.

Question 31

**Bayes’ formula definition**

Answer 31

Bayes’ formula is a method for updating probabilities based on new information.

Question 32

Bayes’ formula equation

Answer 32

Bayes’ formula is expressed as follows: Updated probability of event given the new information = [(Probability of the new information given event)/(Unconditional probability of the new information)] × Prior probability of event.

Question 33

**Multiplication rule of counting**

Answer 33

The multiplication rule of counting says, for example, that if the first step in a process can be done in 10 ways, the second step, given the first, can be done in 5 ways, and the third step, given the first two, can be done in 7 ways, then the steps can be carried out in (10)(5)(7) = 350 ways.

Question 34

**Assign every member of a group**

Answer 34

The number of ways to assign every member of a group of size *n* to *n* slots is *n*! = *n* (*n* − 1) (*n* − 2)(*n* − 3) … 1. (By convention, 0! = 1.)

Question 35

**Multinomial formula**

Answer 35

The number of ways that *n* objects can be labeled with *k* different labels, with *n*₁ of the first type, *n*₂ of the second type, and so on, with *n*₁ + *n*₂ + … + *n**_k* = *n*, is given by *n*!/(*n*₁!*n*₂! … *n**_k*!). This expression is the multinomial formula.

Question 36

**A special case of the multinomial formula is the combination formula. The number of ways to choose *r* objects from a total of *n* objects, when the order in which the *r* objects are listed does not matter, is**

Answer 36

Question 37

**The number of ways to choose *r* objects from a total of *n* objects, when the order in which the *r* objects are listed does matter, is: Permutation formula**

Answer 37