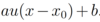Quiz 2: Lectures 6 to 9

Question 1

What is the problem with least squares?

Answer 1

It assumes that the noise distribution is the same for all the points but it is often more complicated since we have inliers and outliers.

Notice:

If we are penalising all point by their squared distance from the line then the outliers will have a huge penality. We sometimes call this huge penality loss which can drive the estimated solution away from the correct solution.

Question 2

Inliers

Answer 2

Points that follow the model

Question 3

Outliers

Answer 3

Points that do not follow the model

Question 4

Hough Transform

Answer 4

1. Define a matrix H that counts the number of votes for a line defined by (r, teta) and initialise H to 0

2. For each (x_i, y_i){
   
   1. For each teta { //choose sampling of tetas
      
      1. r:= round(x_i cos(teta) + y_i sin(teta))
      2. H(r, teta) ++;}}
3. return (r , teta) with most votes

Question 5

In words, what does the Hough Transform do?

Answer 5

The Hough Transforms referst to the transformation from set of points (x_i, y_i) to histogram of votes in the model parameter space (in this case (r, teta))

Question 6

Name the advantages of Hough Transform

Answer 6

• Outliers have little effect on the estimate
• The votes of the outliers will be spread over the (r, teta) space

Question 7

Is it possible to get more than one line with Hough Transform? If yes, how do you pick the correct one?

Answer 7

It might be possible that you get two lines from the Hough Transform. You have to either choose one or accept thare are two correct models.

(See lecture 6 and Matlab for more)

Question 8

RANSAC

Answer 8

Random Sample Consensus

This is often used when there are lots of outliers. It is also often used when the number of parameters of the model is more than 2.

It is capable of fitting a model by suing a minimal number of points. In the case of a line it needs 2.

Question 9

RANSAC algorithm (roughly explained)

Answer 9

Sample a large number of points pairs. For each pair of points find the unique line that passes through both points. Then compare all the remaining points to the lines and qualify the points whose distance is less than a threshold tau to be “near” the line. The set of “near” points is called consensus set for that line model.

Repeat this for a certain number of times. Then choose the model that has the largest consensus set. Finally, use least squares on the consensus set and terminate.

Question 10

RANSAC Algorithm

Answer 10

1. Repeat many times{
   
   1. Randomly select 2 points and fit a line
   2. Examine the remaining points (N-2) and count how many (C) are within tau distance from the line
   3. If C = new max then refit the model useing least squares and save new line model
2. }

See notes p.3 for a more general description.

Question 11

RANSAC Parameters

Answer 11

We have to decide a number of parameters:

• When do we consider an edge on point as part of the consensus?
• When do we stop looking for a better model?

Notice:

The two parameters above are related. If the first one is looser, we might terminate earlier.

Question 12

RANSAC Probability

Answer 12

• Let w be the probability that a randomly sample point is an inliner.
• Suppose we need n points to fit a model
• The probability of all n points being inliers is w^n
• The probability that we fail to find all the inliers is 1 - w^n
• If we run k trials, the probability that we fail to find all inliers in k trials is (1 - w^n)^k
• So if you have some idea of what w is and you have a desired probability z of getting at least one good model then you can estimate the number of trials k by solving z = 1 - (1 - w^n)^k for k

Question 13

Name a limitation to edges

Answer 13

One limitation with edges is that we cannot use them to reliably identify single (isolated) points. This is since edges have well defined intensitygrdient direction and so the intensity is by definition contstant along the edge.

For example, if you compare two different points on a edge, they are difficult to distinguish.

Question 14

Corners

Answer 14

Corners are points that are locally distinctive. They are also called interest points and keypoints. There are not necessarly corners. The word corner just suggests that there are two edges comming together at a sharp angle.

To find the “corners”, we can look at the intensities in a small neighborhood around a point (x_0, y_0). If the intensities in this neighborhood are different from those in a same size neighborhood around (x_0 + delta x, y_0+delta y), then it is a locally distinctive point.

Question 15

How do we find locally distinctive points?

Answer 15

By definition, the intensities at point (x_0, y_0) are locally distinctive if any local shift in the image patch gives you a different patten of image intensities.

To find a corner, we look at the sum of squared differences of intensities of the patch and the shifted patch where the shift of the patch is.

To avoid to restricti ourselves to integer values of delta x and delta y, we approximate I(x+delta x, y+delta y) with Taylor series (first order).

We can then rearrange the equation and compress all that into a single matrix M called second moment matrix.

To give more weight to the center of the matrix, we commonly use a function W(*,*) (typically a Gaussian) such that we end up with a weighted version of the second moment matrix.

Question 16

Second Moment Matrix

Answer 16

Question 17

Structure Tensor

Answer 17

Question 18

Weighted Second Moment Matrix

Answer 18

• Provides information about the geometry of the gradient field in the local neighborhood of (x_0, y_0)
• M is also:
  
  • symmetric
  • positive definite
    
    • no negative eigenvalues
  • can be written as M = VAV
    
    • ​columns v1, v2 of V are the eigenvectors of M and are othonormal
    • A is a diagonal matrix with elements a1, a2

Question 19

Inner Scale

Answer 19

Small standard deviation used when we smooth the imge before taking the gradient.

Question 20

Outer Scale

Answer 20

Big standard deviation coming from the Gaussian weighing M.

Question 21

What is the qualitative relationship between the image intensity pattern in the neighborhood and the eigenvalues and eigenvectors?

Answer 21

• It was found that if the eigenvalues a1,a2 can be ordered a1 >= a2 > 0, then
  
  • if the image intensity is near constant in the neighborhood, then gradients are small and a1 ~ a2~ 0
  • If step edge in intensity in neighborhoods then all gradients are parallel and a1 > 0 but a2~0
  • If gradient pointing to different directions and a1 != 0 and a2 != 0, then found a corner.

Question 22

Name a reason why we would use Harris Corners’ procedure

Answer 22

Notice that in the normal procedure we would solve a quadratic for each pixel to find the eigen values.

Question 23

Harris Corners

Answer 23

Trick:

Det of matrix with eigen values = a1a2

trace = a1 + a2

Question 24

Describe the operator by Brown, Szeliski and Winder

Answer 24

where e is a small positive number that avoids division by 0.

Question 25

Brown, Szeliski, Winder: What happens if the determinant is near 0 but the trace is mch different from 0?

Answer 25

One of the eigenvalues is large and the other near zero.

There must be a strom image intensity gradients in the neighborhood of the point and the gradients would be in only one direction.

Notice: in this case, the second moment matrix could be use to detect edges!

Notice that we will need to do non-maximum suppression to avoid having a clump of points in a neighborhood that are all greater than threshold and hence would all be interest points.

Question 26

TODO Lectures 7 & 8

Question 27

Scale Space

Question 28

How can you make an image appear as if it was far in distance?

Answer 28

• One mathematical model is to blur the image and subsample it

Question 29

What does it mean to subsample?

Answer 29

Subsampling means:

• skip over many pixels
• Notice: Sumsampling is not sufficient. The image do not correspond to what the object looks like when far away.
• By blurring the image first and the subsampling, we are guaranteed that all pixels in the original image will be represented.

Question 30

Gaussian Scale Space

Answer 30

A family of images defined by:

I(x, sigma) = I(x) * G(x, sigma) 1D

I(x,y; sigma) = I(x,y) * G(x,y;sigma) 2D

Notice the images are indexed by the amount of blur defined by sigma

Question 31

Discretize

Answer 31

Represent or approximate a quantity or series using a discrete quantity or quantities.

Question 32

What do we have to discretize when building a scale space?

Answer 32

We have to discretize the pixels (x,y) and the set of scale sigma.

To discretize sigma, we can choose a sequence os scales using arithmetic progression or, a more common approach, is to use a geometric progression such as

sigma = s0, 2s0, 4so,…

Question 33

Octave

Answer 33

In the case where

sigma = s0, 2s0, 4s0, 8s0,…

where s0 = 1 and so sigma = 1,2,4,8,..

each doubling of the scale is called octave

Question 34

Arithmetic Progression

Answer 34

Sequence of numbers such that the difference of any two successive numbers is constant.

Question 35

Geometric Progression

Answer 35

Sequence of number where when each terms after the first is found by multiplying the previous number by a fixed non-zero number called common ratio.

In the example where sigma = s0, 2s0, 4s0, 8s0,…

the common ratio is 2 as we do:

1*2 = 2

2*2 = 4

4*2 = 8

Question 36

Blurring:

How would you sample the sigma dimension in scale space if you are given an image I(x,y)

Answer 36

I(x, y, 0) = I(x,y)

I(x, y, 1) = I(x,y) * G(x,y,sigma=1)

I(x, y, 2) = I(x,y) * G(x,y, sigma=2)

I(x, y, 4) = I(x,y) * G(x,y, sigma = 4)

…

I(x, y, 2^k) = I(x,y) * G(x,y, sigma = 2^k)

Notice: Each of these blurred images are the same size of the original image!

Question 37

Gaussian Pyramid

Question 38

What happens when you blur with a sigma larger?

Answer 38

We get an image whose intensities values vary more gradually accros (x,y)

Question 39

True or False

We need less samples to get a good approcimation of a more blurred image.

Answer 39

True

This can be done with the Gaussian Pyramid

Question 40

One claim is that we can use less samples to approximate a blurred image. How can we sample the images?

Answer 40

We can define a sequence of images that each have successfully half as many pixels in the x and y dimensions as their predecessor.

I(x,y) = I(x,y,0)

I₁(x,y) = I(x,y,1)

…

I_k(x,y) = I(2^kx, 2^ky, 2^k-1 )

Question 41

What is the most common way to compute the Gaussian Pyramid?

Answer 41

The most common way to compute the Gaussian Pyramid is to alternate between the blur and the subsample operations:

1. Blur with sigma = 1
2. Subsample with step = 2 => I₁
3. Blur I₁ with sigma = 1 to get I₂
4. Subsample I₂ with stride = 2
5. …

Question 42

Recall the problem of finding the shift between two images. Recall that we used Taylor Series and that the algorithm did not work for large distances (shifts), why?

Answer 42

This is because if the distance was too big, we could easily get stuck in a local minima of the squared error function.

Question 43

Recall the problem of finding the shift between two images. Recall that we used Taylor Series and that the algorithm did not work for large distances (shifts).

How can we solve this problem with Gaussian Pyramid?

Answer 43

Notice that the Gaussian Pyramid allows you to work with smaller subsamples of the original images. This makes the distance in shift smaller.

Steps:

1. Compute the Gaussian of both images I and J
2. Run the LK algorithm at a higher lever of the pyramid(s) first. This is where the number of pixels is small and the images are heavily blurred

Notice: At this point 1 pixel at sigma = 2^k = 2^k pixels in original

Question 44

Coarse-to-fine

Answer 44

Begin with an estimate of h at some chosen high level of the pyramind. Then, as we go down the pyramid, we can redifine h.

Question 45

What are two benefits from applying LK on the Gaussian Pyramis of the images I and J?

Answer 45

1. Running the LK on smaller images allow us to obtain sparse estimates quickly
2. If some of the vectors in h in the original image are large, then, these vectors will be a factor of 2^k smaller at level k.
   
   1. LK will be more able of estimating them without getting stuck

Question 46

What is this equal to?

Answer 46

G(x, sigma)

Question 47

Recall that the derivative is a convolution and that the convolution is commutative.

Find what the second derivative of a Gaussian is equal to when convoluted with u(x) (unit step function).

Answer 47

Question 48

Let u(x) be a unit step function,

proof that u(x) * df(x)/dx = f(x)

Answer 48

See Lecture 9, page 6

Question 49

Consider the function in the image:

At what values of x does the function have a positive and a negative peak?

How do you find this?

Answer 49

• Positive peak: x = -sigma
• Negative peak: x = sigma

You can find this by finding the derivative, set to 0 and solve for x

Question 50

Consider the equation in the image, notice that is you plug

x = +/- sigma

you get the height of the positive and negative peaks. How can you make the height independent of sigma?

Answer 50

We would have to use the following filter since we would cancel sigma with 1/sigma²

Notice that because of this independende we call this the normalised Gaussian second derivative

Question 51

Consider the shifted edge by x₀ in the image

How does a and b affect the function?

Answer 51

a multiplies the height of the peaks by a

b has no effect since the derivative of a constant is 0

x₀ shifts the peaks by x₀

Question 52

Read paragraph 1 on Lecture 9 p5

Question 53

Define a box function

Answer 53

Question 54

How can you define the box function in terms of the unit step function?

Make drawings so that you understand how it works

Answer 54

Question 55

Lecture 9 p.5 read highlighted parts