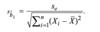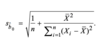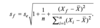Quantitative Methods 1 Flashcards
Required rate of return/interest rate
Future Value
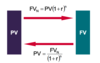
Calculating stated (nominal) and effective rates from periodic
Computing effective rates from periodic rate
Future value formula with more than one compounding period
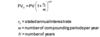
FV/PV based on continuous compounding
PV of a perpetuity
Annuity Due
Payments paid at the beginning of period
Ordinary annuity
Cash flows made at the end of each period
Nominal Scale (4th strongest)
Data is only categorized
Ordinal Scale (3rd Strongest)
Data is categorized and ranked
Interval Scales (2nd Strongest)
Data is categorised, ranked, and evenly spaced
Ratio scales (1st Strongest)
Strongest level of measurement. Categorized, ranked, evenly spaced, natural zero
Steps to producing frequnecy distribution
- Sort data into ascending order
- Calculate range of data
- Decide on number of intervals (k) and interval width (Range/k)
- Determine intervals by successively adding width to minimum value
- Count number observations falling in each interval
- Construct a table showing number of observations falling into each interval
Cumulative frequency
Absoluted frequencies added up as we move from first to last interval
Relative frequency
Absolute frequency of each interval divided by total number of observations
Cumulative relative frequency
Adds up relative frequencies as we move from first to last interval. Fraction of observations that are less than upper limit of each interval
Histogram
Graphical presentation of absolute frequency distribution
Frequency Polygon
Graph midpoint of each interval on horizontal axis and absolute frequency on vertical; draw a line graph
Geometric mean
Mean absolute deviation
Variance
Standard deviation/Varaince calculator
Quartile calculation
Harmonic mean (same as money weight)
Coefficient of variation
Negatively skewed
Positively skewed
Semivariance
Measure of dispersion below the mean. Average of squared differences between observations below the mean and mean value. Important as investors are concerned with deviations below the expected value. If symmetrical distribution semivariance = variance
Target semivariance
Calculated dispersion below a specified target instead of mean
Chebyshev’s Inequality
Coefficient of variation
1 s.d. coverage
68%
95% of observations
95%
99% of observations
2.575 s.d.
Skewness formula
Kurtosis charts
Kurtosis interpretation
Only data values that are outside the region of the peak contribute to kurtosis. High values are obtained where the probablility mass is concentrated around the mean.
Calculating combinations and permutations
Can be done on calculator
Variance and S.D. with probablilities
Calculator probability, expected return, and variance of return
Covariance
Correlation
Binomial distribution
Standard deviation of a two-stock portfolio
Coefficient of determination
Degrees of freedom for F statistic
n - 2
F Statistic for Linear Regression
Analysis of Variance Table
Standard Error of Estimate
Standard error of slope
Where Se is the standard of the estimate
One sided test for slope/correlation
Standard Error of Intercept
Steps in Testing Intercept
Standard Error Forecast
Multinomial Formula
Contingency/Confusion Matrixes
To find expected number
(Total Row i x Total Column j)/Total Overall
A priori Probability
Probability based on objective proabilities, using deduction and reasoning
Example with a coin flip, using the binomial proability function to calculate find the odds of getting heads 3 times
Calculating quartiles/percentiles
- Think as percentile
- Ly = (n. observations + 1)*percentile/100
Second method for quartiles (generalised)
(n. observations + 1)* (% of population below this)
If it is the 80th percentile, 80% of population below this
LINEAR INTERPOLATION
