Quant Mixed Practice (Use Paper)

Question 1

There are 5 women and 4 men. How many different teams of 2 women and 2 men are possible?

Answer 1

Count the women pairs and men pairs separately, then multiply for the total.

Women: 5 * 4 / 2 = 10

Men: 4 * 3 / 2 = 6

10 * 6 = 60

Question 2

There are 9 candidates for 4 positions on a committee. How many different committees are possible?

Answer 2

126

out of 9, pick 4

4 slots on top, then divide by 4!, because the order doesn’t matter.

Question 3

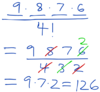
6 athletes are competing for gold, silver and bronze medals, plus 1 honorable mention. How many different ways can the awards be distributed?

Answer 3

This time, the order matters, so we don’t divide by “4!”

4 Slots (for gold, silver, bronze, honorable mention) –> 6*5*4*3 = 30*12 = 360

Question 4

What is the sum of the odd integers from 5 to 25, inclusive?

Answer 4

“inclusive” means including 5 and 25.

Sum = Number of values (N) * Average Value

= N * (First + Last) / 2

N = (Last - First) / Increment + 1

= (25 - 5) / 2 + 1 = 20/2 + 1 = 11

Sum = 11 * (5+25) / 2 = 11 * 15 = 10*15 + 15 = 165

Question 5

Mary spent a total of $10,000 on supplies, taxes, and rent last year. How much did she spend on rent?

(1) The amount spent on rent was 50 percent of the amount spent on taxes and supplies.
(2) The amount spent on supplies was 1/3 of the amount spent on taxes and rent

Answer 5

A- (1) Alone

DON’T CALCULATE!

Rephrase: 10,000 = S + T + R, R = ?

If we have 2 more unique equations, or 1 equation that has the combo “S + T”, it’s sufficient!

(1) R = .5(T + S) –> 2R = S + T –> Can substitute S + T into the equation, and solve for R.
(2) S = 1/3 (T + R). This time, we can’t isolate “S+T”. Insufficient.

Question 6

The number of pens that Joe and Mary had were in a 2:3 ratio. After Mary gave Joe 6 pens, Mary had 3 pens for every 7 that Joe had. After this gift, Joe had how many more pens than Mary?

Answer 6

8

Start with unknown multiplier: Joe / Mary = 2x / 3x

Then, we add 6 to Joe, and subtract 6 from Mary, to create an equation with the new ratio.

Make sure to put the ratio in the correct order: The new ratio is 7/3

Cross-multiply and solve for x.

Make sure to answer the question asked!

Plug in x –> (2x + 6) / (3x - 6) = 14 / 6 –> 14 - 6 = 8

Question 7

A boat was sold at a loss of 40% of the purchase price. Another boat was sold at a profit of 20% of the purchase price. If each boat was sold for $30,000, what was the total profit or loss combined?

Answer 7

Let C = Cost ; calculate separately

Loss: 30,000 = (100% - 40%) * C

30,000 = .6C = 3/5 C

Divide by 3/5 –> Multiply by 5/3 –> C = 50,000 –> Loss = 20,000

Profit: 30,000 = (100% + 20%) * C = 1.2C = 6/5 C

C = 25,000 –> Profit = 5000

Combined, 20,000 - 5,000 = $15,000 Loss

Question 8

Answer 8

Find the ratio of boxes loaded– night crew : day crew

3/4 the speed, 4/5 as many workers

3/4 * 4/5 = 3/5 = night crew : day crew.

Read carefully! Question asks what fraction of the TOTAL is the day crew

5 / (3+5) = 5/8

Question 9

Shirts were sold for $20 more than the cost. They were sold at a profit of 40% of the purchase price. The total revenue from shirt sales was $2800. How many shirts were sold?

Answer 9

40

C = Cost or Purchase Price S = Sales Price

20 = 40% * C

20 = 2/5 * C

C = 50

S = 50 + 20 = 70

Revenue = Sales Price * Number sold –> R = SN –> N = R/S

2800 / 70 = 40

Question 10

If n is a positive integer and the product of all the integers from 1 to n, inclusive, is a multiple of 2^8, what is the least possible value of n?

Answer 10

10

“The product of all integers from 1 to n” translates to n! (n factorial)

We need to find the lowest factorial that includes 8 total 2’s as factors.

Question 11

Machine type A does a job in 8 hours, while machine type B does a job in 12 hours. If 2 machines of type A are used, how many machines of type B are needed to complete the job in 90 minutes?

Answer 11

Calculate the Work separately for A and B:

A: N = 2, R = 1/8, T = 90 minutes = 3/2 hours

W = NRT = 2 * 1/8 * 3/2 = 3/8

So, work remaining for type B is 1 - (3/8) = 5/8

B: 5/8 = N * 1/12 * 3/2

5/8 = N * 1/8 –> N = 5

Question 12

There were 3 plums and 4 lemons. After more of each were added, the ratio of plums to lemons was 2:1. How many lemons were added?

(1) A total of 8 plums and lemons were added
(2) The number of plums added is 5 more than twice the number of lemons

Answer 12

A: (1) Alone

Define variables and translate:

P = plums added, L = lemons added. Solving for L.

(3+P) / (4+L) = 2/1

Need 1 more unique equation to solve.

(1) P + L = 8 Unique equation –> Sufficient
(2) Trap! Same as the info in the prompt, not a unique equation!

Cross-multiply the prompt equation to check if it’s the same as (2)

P = 5 + 2L

Question 13

An integer between 1 and 66 is chosen at random. What is the probability that n(n+1) will be divisible by 6?

Answer 13

Pattern will repeat every 6 numbers, up to 66.

“Divisible by 6” means “has both 2 and 3 as factors”

Easiest way is to create a chart:

4/6 = 2/3

Question 14

N is 3 times the average of 15 numbers. In terms of N, what is the average of all the numbers, including N?

Answer 14

Let A = average of the 15 numbers

N = 3A –> A = 1/3 N

It asks for the average of all 16 numbers : (N + 15A) / 16

Substitute for A –> N + 5N / 16

6N / 16 = 3/8 N

Question 15

Mary drives at a speed of 66 feet/second. How many miles away is she from her home, if it will take her 3 hours to reach home? (Given 1 mile = 5280 feet)

A) 25

B) 80

C) 135

D) 210

E) 300

Answer 15

c) 135

RT = D ; T = 3 –> 3R = D

Need to convert from feet/second to miles/hour. Set it up so units cross out on top and bottom, to avoid mistakes. (see image below)

If we notice the answer chioces are quite far apart, we can approximate, instead of calculating exactly!

3600/5280 is approximately 2/3 –> 2/3 * 66 = 44 mi/hr. (3600/5280 simplifies to 15/22 –> you can verify this as practice, but if we can approximate and save time that’s great)

3R = D –> 44*3 = 132 –> C

Question 16

If there are 3 green marbles, 2 yellow marbles, and 5 red marbles.

If 2 are selected without replacement,

A) what is the probability they are both red?

B) What is the probability of 1 green, 1 yellow?

Answer 16

There are 2 events, so we multiply the probabilities for picking each marble.

There are 10 total marbles to start, and 9 after picking one, so these are our denominators.

A) 1st red 5/10 , 2nd red 4/9 –> 5/10 * 4/9 = 1/2 * 4/9 = 2/9

B) This time, there are 2 options:

1st green 3/10, 2nd yellow 2/9 –> 3/10 * 2/9 = 1/15

1st yellow 2/10, 2nd green 3/9 –> 2/10 * 3/9 = 1/15

Total is 1/15 + 1/15 = 2/15

Question 17

Is the probability greater than 50% that a student randomly selected will be a female with brown hair?

(1) 1/2 of the students are female
(2) 1/2 of the students have brown hair

Answer 17

D - Each Alone

If the question asked for the probability VALUE, we couldn’t find it.

But since it asks for YES / NO, we can definitively say NO for each statement.

The BOTH box on matrix (or green “Intersection” on Venn Diagram) can’t be greater than the total female or total brown hair!

Question 18

Is the probability less than 40% that a student randomly selected will be a female with brown hair?

(1) 1/2 of the students are female
(2) 1/3 of the students have brown hair

Answer 18

B - (2) Alone

Could convert fractions to percents for easier comparison: 1/2 = 50%, 1/3 is about 33%.

(1) Maximum for Both is 50%. Could be YES or NO. Insufficient
(2) The maximum for Both is 1/3 –> Must be YES –> Sufficient.

The Both box on matrix can’t be greater than the Total for brown hair!

Question 19

Joe passed a store while traveling east at a constant speed of 30 miles per hour at 3pm. 30 minutes later, Kate passed the same store while traveling east at a constant speed of 36 miles per hour. At what time would Kate catch up to Joe?

Answer 19

How far ahead is Joe? 30 minutes ahead –> convert to a distance

Convert 30 minutes to 1/2 hour

30 mph * 1/2 = 15 miles ahead

We can use relative rates: since they are heading the same direction, we find the difference:

Kate is catching up at a rate of 36-30 = 6mph

T = D/R = 15 miles / 6mph = 2.5 hours (from the time KATE passes the store)

Be careful not to miss a step: Joe passes the store at 3pm, so Kate passes it at 3:30.

3:30 + 2.5 hours = 6pm

Question 20

Of 400 athletes, 160 neither ran nor jumped, and 120 jumped. For every athlete that did both, 3 only ran. What percentage of athletes both ran and jumped?

Answer 20

We want “Both”. So define x as “Both”.

Then, 3x goes in “only ran”.

400 - 120 = 280 in “Not J” box

Solve for x: 3x + 160 = 280 –> 3x = 120 –> x = 40

40 / 400 = 10%

Question 21

Real estate expenses accounted for 40% of operating expenses. There were $8 million of rent expenses, or 1/4 of the real estate expenses. How many million dollars were operating expenses?

Answer 21

8 = 1/4 Real Estate Expenses (REE)

REE = 32

32 = .4 Operating Expenses (OE)

Easiest if you recognize .4 as 2/5 –> multiply by 5/2 on both sides.

32*5/2 = 80 million dollars

Question 22

In the sequence 3, 9, 27, 81, … each term after the first is three times the previous term. What is the 10th term minus the 9th term?

A) 3⁹

B) 2 * 3⁹

C) 3⁸

D) 2 * 3⁸

Answer 22

B) 2 * 3⁹

1st term is 3¹.

Following the pattern, 10th term is 3¹⁰, 9th term is 3⁹

So, find 3¹⁰ - 3⁹

Factor out 3⁹ –> 3⁹ (3 - 1)

2 * 3⁹

Question 23

If 4*2^x + 2^x+4 = 10*2^2y, what is y in terms of x?

Answer 23

Product Rule of Exponents: 2^x+4 = 2^x * 2⁴

Factor out 2^x –> 4*2^x + 2^x * 2⁴ = 2^x (4 + 2⁴) = 20 * 2^x

Divide by 10 on both sides: 20 * 2^x = 10*2^2y —> 2*2^x = 2^2y

Use product rule again: 2*2^x = 2^2y –> 2^x+1 = 2^2y

x + 1 = 2y

y = (x+1) / 2

Question 24

3/4 of the men is equal to 1/6 of the total number of adults.

What is the ratio of women to men?

Answer 24

3/4 M = 1/6 A

Multiply by 4/3 on both sides –> M = (4/3) * (1/6) A = 2/9 A

If M = 2/9 A, then women are all the rest –> W = 7/9 A.

Ratio of women to men is 7:2

Question 25

How many positive integers between 50 and 150 are multiples of 3 and 4?

Answer 25

Note that “between” means NOT inclusive, unless specifically stated that it is inclusive.

If it’s BOTH a multiple of 3 and 4, we find the LCM of 3 and 4. So, it must be a multiple of 12.

(Last - First) / Increment + 1

First = 60

Last = 144

(144 - 60) / 12 + 1 = 84 / 12 + 1 = 7 + 1 = 8

Question 26

Solve | 3x - 2 | = 4

Answer 26

Need to split into 2 equations:

A) 3x - 2 = 4

3x = 6 –> x = 2

B) If it’s negative, it flips sign.

Make sure to put negative outside of parenthesis

• (3x - 2) = 4 –> -3x + 2 = 4
• 3x = 2

x = -2/3

Question 27

There were twice as many pets as adults and 4 times as many women as men. If there was a total of 60 men, women, and pets, how many women were there?

Answer 27

“twice as many pets as adults” –> 1/3 were adults –> 20 adults

4 times as many women as men –> 4/5 women

4/5 * 20 = 16

Question 28

Working alone, pump X pumped out ¼ of the water in a tank in 2 hours.

Then pumps Y and Z started working and the three pumps together pumped out the rest of the water in 3 hours.

If pump Y, working alone, would have taken 18 hours to pump out the rest of the water, how many hours would it have taken pump Z, working alone, to pump out all of the water?

Answer 28

R = W / T

R_x = (1/4) / 2 = 1/8

Combined: “rest of tank” –> 3/4 of tank in 3 hours

R_x + R_y + R_z = (3/4) / 3 = 1/4

3rd sentence says R_y = (3/4) / 18 = 1/24

R_z = 1/4 - R_x - R_y

Find common denominator of 24

Rz = 6/24 - 3/24 - 1/24 = 2/24 = 1/12

12 hours

Question 29

Joe bought a bike for $120 and then sold it for a 75 percent profit. If Joe sold it at a 1/8 discount off the original retail price, approximately what was Joe’s profit as percentage of the original retail price?

A) 22%

B) 28%

C) 33%

D) 38%

E) 45%

Answer 29

D: 38%

75 percent profit * 120 = 90

90 + 120 = 210 Selling price

Sold at a 1/8 discount –> 7/8 Retail price = 210

Retail price = 8/7 * 210 = 240

90 / 240 = 3/8 = 37.5% –> closest to 38%

Question 30

A) What are “roots”?

B) What are the roots of 2x² + 3x = 2?

Answer 30

A) Roots translates to “x =”

Roots are the values for x that solve a quadratic.

If we have the equation (x - r) (x - s) = 0, the roots would be r and s.

B) Subtract 2 to get 0 on the right side: 2x² + 3x - 2 = 0

Factor: (2x - 1) (x + 2) = 0

Roots are the solutions for x: 1/2 and -2

Question 31

Which of the following equations has -1 + √2 as one of its roots?

A) x² + 2x – 1 = 0
B) x² – 2x + 1 = 0
C) x² + 2x + 1 = 0
D) x² – 2x – 1 = 0
E) x² – x – 1= 0

Answer 31

“roots” translates to x = -1 + √2

x + 1 = √2

square both sides: (x + 1)² = 2

x² + 2x + 1 = 2

A) x² + 2x - 1 = 0