QSAR Flashcards
1
Q
Quantitative Structure-Activity Relationship
A
- What are they
- Molecular Geometry
- 3D structure optimisation
- Molecular descriptors
- The process of QSAR analysis
2
Q
QSAR- the principle
A
- You have at your disposal a set of existing compounds where the biological activity has already been measured
- How can you use this information to decide which compounds to make and test next
- draw the structures of the compounds and optimise their 3D geometries
- Calculate molecular properties
- Use the descriptors together with the biological data to derive equations that predict the biological activity
- Calculate the descriptors for new compounds and use the equation to predict their biological activities
3
Q
Important note
A
- QSAR does not require any knowledge of the receptor, active site or mechanism of action
- Only the structure of a set of compounds of known biological activity are required
- It is necessary, however, that the compounds all act in the same way at the same receptor or active site
4
Q
General procedure
A
- Select a set of molecules interacting with the same receptor with known activities =>
- Calculate features (e.g. physicochemical properties)
- Divide the set into 2. One for testing and on for training
- Training set: Build a model- find the mathematical relationship between the activities and properties
- test the model on the test dataset
- Testing set:
5
Q
Preparation of the structures (structures of known biological activity)
A
- Draw the compounds
- Clean up the structure of performing a molecular mechanics geometry optimisation
- Change the geometry to minimise the energy of the molecule
- Identify key rotatable bonds and perform a conformation search**
- Perform a semi-empirical quantum mechanical (calculate energy difference once the confirmation has occurred- if the energy lowers it is more correct) geometry optimisation on the lowest energy conformation identified in step 3
- NB** see molecular mechanisms geometry optimisation
6
Q
Molecular mechanics geometry optimisation
A
- Considers atoms as balls and bond as springs
- Does not consider the electrons
- Fast
- Low quality but OK for a quick clean up of a drawn structure
7
Q
Semi-Empirical quantam mechanical geometry optimisation
A
- The valence electrons (outer shell- governs bonding of the molecule) are used to construct molecular orbitals
- The inner electrons are approximated via a parameter set
- Slower than MM (molecular mechanics) but much better quality
- Several hours per molecule
8
Q
Why is conformation important
A
- At room temperature, the lowest energy conformer prevails
- We want the molecular properties to be calculated from a relevant conformation
*
9
Q
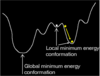
Which conformation should be used
A
- All energy minimisation techniques concentrate on searching downhill- they therefore tend to find the nearest local minimum on the energy surface
- If a much deeper (i.e. better) energy minimum is nearby, but separated from the starting point by a high energy barrier, it will not be found
- Energy minimization is therefore not capable of finding the global energy minimum. Therefore we must use conformation searching
- NB- most drugs conformation they have when they are active tend to be the same as those in the global minimum energy conformation
10
Q
Conformation searching
A
- Each rotatable in turn bond is stepped round in small increments and the energies of the resulting conformations are calculated
- This is used to find the approximate position of the GLOBAL MINIMUM ENERGY POTENTIAL WELL
- After that a high quality energy-minimisation technique can be used to refine the structure down to the global minimum energy conformation (E.g. Semi-empirical quantum mechanical geometry optimisation)
11
Q
Conformation searching- Exhaustive searching of rotatable bonds
A
- Conformational explosion
- 1 rotatable bond/ 5 steps => 72 conformations
- 2 rotatable bonds/ 5 steps => 5184 conformations (722)
- 8 rotatable bonds/ 5 steps => 722204136208736 (728)
- Potential energy surface from 2 search labels
- Cannot be done for drugs with many rotatable bond due to the large amount of time it would take to complete
12
Q
A
- Input the 3D structure
- Align the molecules about their common core (because some properties are vectorised)- define what the core is
- Add the biological activity
- Calculate the molecular descriptors
- Use multiple regression analysis to derive an equation relating the biological activity to the calculated properties
13
Q
Molecular descriptors- examples DONT NEED TO REMEMBER ALL OF THESE
A
14
Q
Molecular descriptors- examples
A
- Consititutional
- Geometrical
- Topological
- Electrostatic
- Quantum-chemical
- Miscellaneous
- Solubility
- Electronic
- Lipophilic
- Steric
15
Q
Molecular descriptor- examples
A
16
Q
Molecular descriptors-
A
- Some descriptors can be calculated rapidly e.g. MW, dimensions
- Other descriptors may be time-consuming to calculate such as those derived from Quantum mechanics (Anything that involves electrons)
- HOMO-LUMO energy gap
- Polarisability
- Partial atomic charge
- Some descriptors have an obvious experimental counterpart with which the calculation can be compared e.g. partition co-efficient
- Other descriptors refer to properties of the whole molecule; others refer to the properties of individual atoms
- New descriptor - modern software packages allow you to generate hundreds or even thousands descriptor. Not all of them are useful, for examples dragon provides 1664 mol descriptors
17
Q
Molecular descriptors 2D and 3D
A
- Some descriptors may be calculated from the 2D structure whilst others require the 3D structure
- If a 3D structure is required then which molecular conformation should be adopted => Usually the global minimum energy conformation
- Some descriptors such as lipole, dipole, moments of inertia have components along the orthogonal x,y,z axes (i.e. they are vectors)
- Thus to compare the values from one molecule to another, each molecule in the set must be orientated in the same way
18
Q
Molecular descriptors 2D and 3D- definition
A
- Mass- the molecular mass is calculated assuming that the various atomic isotopes occur in their common proportions
- Surface area- connolly surface area- probe radius of 1.4Å
- Volume- the volume within the surface area defined by the van der waals radii of the atoms
19
Q
Molecular descriptors 2D and 3D
Moments of inertia and ellipsoid volume
A
- A measure of the distribution of mass within a molecule
- The moments of inertia and prinicipal axes of inertia for a molecule are calculated using the inertia tensor
- These results are reported in TSAR as moment 1 size, moment 1 length
- The volume defined by these values is calculated and reported as the ellipsoid volume
- You can view the molecule and an ellipsoid of inertia
- The ellipsoid’s prinipal axes are aligned with the aces of the inertia tensor. The length of each axis is inversely proportional to the moment of inertia around that axis
- The resulting ellipsoid is then scaled so that the atom furthest from the centre of gravity of the molecule appears on the ellipsoid surface
20
Q
Molecular Descriptors 2D and 3D
LogP
A
- Lipophillicity is a measure of the ability of the molecules to move between fat and water
- It is often used to indicate how easily a molecule may be transported across membranes
- Most people use the partition co-efficient for water/octanol (LogP) as an estimate of lipophillicity
- Atomic values or substituent values are available from a databaser of experimentally determined values
- The values for the appropriate atomic or substituent fragments are simply added together to derive the molecular LogP value
21
Q
Molecular Descriptors 2D and 3D
Molar refractivity
A
- This is compiled by reference to a database of experimentally determined values- substituent contributions and atomic contributions to molecular molar refractivity values
- MR often shows a strong correlation with ligand binding
- Both LogP and MR increase with alkyl chain length, so log P and MR show a strong correlation
- Polar functional groups increase MR, but decrease logP. Perhaps MR is a measure of non-lipophilic interactions, while logP is a measure of lipophilic interactions
- MR has a strong correlation with the molecular polarisability
22
Q
Molecular Descriptors 2D and 3D
Polarizability
A
- A measure of the ease with which the electron cloud of the molecule can be distorted by an applied electric field
- The attractive part of the van der Waals interaction is a good measure of the polarisability
- Highly polarisable molecules can be expected to have strong attractions with other molecules
- The polarisability of a molecule can also enhance aqueous solubility
23
Q
Molecular Descriptors 2D and 3D
Dipole moment
A
- Dipole moment calculations use partial charge information
- Total dipole moment for whole molecules and substituents are calculated using the centre of charge as an origin, and are in Debye units
24
Q
Molecular Descriptors 2D and 3D
Lipole
A
- The lipole of a molecular is a measure of the lipophilic distribution
- It is calculated from the summed atomic logP values, as dipole is calculated from the summed partial charges of a molecule
- The total lipole for whole molecules and substituents is calculated using the centre of logP as an origin
25
Q
Molecular Descriptors 2D and 3D
Verloop substituent parameters
A
- Verloop preposed a set of multi-dimensional steric parameters to help explain the steric influence of substituents in the interaction of organic compounds with macromolecules or drug receptors
- Verloop parameters calculation assume that all atoms have Van der Waals radii and use these to define the substituents space requirements
- The 5 verloop parameters define a box that can be used to characterize the shape and volume of the substituent
26
Q
Molecular Descriptors 2D and 3D
Verloop substituent parameters continued
A
- L, the length parameter- the maximum length of the substituent along the axis of the bond between the first atom of the substituent and the part molecule
- B1, the width parameter- the smallest width of the substituent in any direction perpendicular to L
- B2,3,4 are determined by measuring the width of the substituent, as follows
- In the direction opposite to the axis defined by B1
- In the 2 direction perpendicular to this axis and the original bond axis
- The 5 verloop parameters define a box that can be used to characterize the shape and volume of the substituent
27
Q
Molecular Descriptors 2D and 3D
Topological, connectivity, electropographical and shape indices
A
- Many of the descriptors which can be calculated from the 2D structure rely upon the molecular graph representation bevause of the need for rapid calculations
- Several of these descriptors have been developed which characterise some aspect of molecular shape, connectivity or atom distribution as a single number
28
Q
Constructing the QSAR
(Relating the biological activity to the calculated properties)
A
- Use multiple regression (an extension of linear regression)
- This calculates an equation describing the relationship between a single dependent y variable and several explanatory x variables
- It is very important to choose variables (calculated properties) that are not correlated
- Multiple regression is the usual approach but there are others
29
Q
Techniques employed in quantitative structure- property relationship (QSRP) studies
A
- Multiple linear regression analysis (MLRA)
- Free-Wilson analysis
- Cluster analysis
- Pattern recognition
- Factor analysis
- Discrimination analysis
- Principal component analysis (PCA)
- Partial least square (PLS) analysis
- Comparative molecular Field analysis (CoMFA)
- Artificial neural network (ANN)
- Evolutionary algorithms, such as genetic function approximation (GFA)
30
Q
Constructing the QSAR
Some regressions
A
- Simple multiple regression- all the input x variables (circulated properties) are used in the equation to predict y (the bio-activity)
- Stepwise multiple regression- a selection algorithm is used to choose a subset of input x variables
31
Q
Constructing the QSAR
Multiple regression
A
- Multiple regression calculates an equation describing the relationship between a single dependent y variable and several explanatory x variables
- a1,a2 etc and c are constants chosen to give the smallest possible sum of least squares difference between true y values and the y’ values predicted using this equation
- y= biological activity
- x1= calculated molecular properties
32
Q
Constructing the QSAR
Is it reliable
A
- Having derived an equation for predicting y from a series of independent variables, one needs to know how reliable predictions made with this equation are likely to be
- The multiple correlation co-efficient r2 describes how closely the equation fits the data
- If the regression equation dascribes the data perfectly then r2 will be 1.0
33
Q
Constructing the QSAR
Overfitting
A
- The major drawback of regression analysis is the danger of overfitting
- This is the risk that an apparently good regression equation will be found, based on a chance numerical relationship between the y variable and one or more the x variables, rather than a genuine predictive relationship
- The QSAR equation will fit the training data very well but be useless in predicting the activity of a compound not in training set
34
Q
Constructing the QSAR
Dangers of overfitting
A
- When an overfitted model is used predictively, the predicted values for untested compounds will not be an accurate prediction of the true values (when these are eventually determined)
- Thus the regression equation has NO predictive power
- Use a of cross-validation technique to estimate the true predictive power of energy regression model
- The best way to avoid an overfitted regression equation is to use just a few carefully selected (non-correlated) x variables, and use as many data points as possible (at least 5 per term in the equation)
35
Q
Cross validation of results
A
- Cross validation provides a rigorous internal check on the models derived using regression, discriminant or patial least squares analysis
- It is used to give an estimate of the true predictive power of the model i.e. how reliable predicted values for untested compounds are likely to be
- leave out one row- Each row is left out in turn, so that the value of each row is predicted from all others
- Leave out groups of rows- Groups of rows are left out, excluding a thrid of the data from each model in a fixed pattern
36
Q
Cross validation of resilts
Continued
A
- By default, TSAR leaves out groups of rows in a fixed pattern, using three cross validation groups of rows
- A third of the data is deleted and the values of these rows predicted using the rest of the data
- This is repeated for the second and then the third groups
- The model is judged based on these predictions
37
Q
Constructing the QSAR
r2(CV)
A
- R2(CV) is derived from cross validation. It is the cross validated equivalent of r2
- This is a key measure of the predictive prower of the model
- The closer the value is the 1.0 the better the predictive power
- For a good model r2(CV) should be only slightly lower than r2
- If r2(CV) <<r>2 then there is probably overfitting</r>
38
Q
A
