Q2: Fractions, Decimals, Percents Flashcards
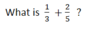
For adding & subtracting fractions, first find a common denominator (Least Common Multiple of 3 and 5)

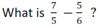



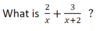
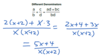
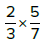
Multiply horizontally:
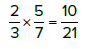
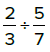
Dividing fractions: Flip the 2nd fraction and multiply
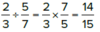

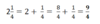
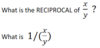
When we take the RECIPROCAL, we flip the fraction
This is the same as 1 divided by the fraction.
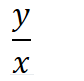
Write “z is x percent of y” as an equation
Percent means “divide by 100”
“of” means “multiply”
“is” means =

Write “x is 20% greater than y” as an equation
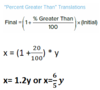
Write “x is 15% less than y” as an equation,
a) write using a decimal
b) convert to a fraction

Write “x is n percent greater than y” as an equation
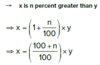
A bike was $50, and is now on sale for $32. What is the percent change in price?

Distribute:
-3(x-7)
= -3*x + -3*-7
= -3x + 27
Be careful with your SIGNS! Double negative turns into a positive
Factor out the Common Factor:
4x + 4y =7
Both terms have “4” as a factor.
So, we can factor it out (this is the inverse process to “distribution”)
4(x+y) = 7
Factor out the Common Factor:
3x + 6y + 15z = 7
Factor out the Common Factor:
The common factor between 3, 6, and 15 is 3.
(we can prove this by writing the prime factorization: 6=2*3, 15=5*3)
We factor out 3 from each “term”.
3(x + 2y + 5z)
Multiplying Exponents:
What is 23 * 24 ?
27
When we multiply exponents with the same bases, we add the powers
ab * ac = ab+c
What is 2 * x3 * y2 * 3 * y4 * x ?
We match up what can be simplified:
2*3 = 6
x3 * x = x4
y2 * y4 = y6
6x4y6
Distribute: -2x(-3x + 5)
- 2x * -3x = 6x2
- 2x * 5 = -10x
6x2 - 10x
Factor out the Common Factor:
15x2 - 10x
This time, we can factor out both a number and a variable:
The common prime factor of 15 and 10 is 5.
The common variable is x
So, we factor out 5x:
5x(3x-2)
Scientific Notation:
Write out as a number: 2.3 * 107 = ?
23,000,000
* 107 is like multiplying by 10, 7 times. This moves the decimal point 7 places to the right.
What is the units digit, tens digit, and hundreds digit of the number 5318?
units: 8
tens: 1
hundreds: 3
What is the units digit of 3219 ?
We need to find the pattern.
3219 will have the same units digit as 219
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
The pattern repeats for every 4 numbers in the pattern: {2, 4, 8, 6}
Every 4th power will have a units digit of 6: 24, 28, 212, 216
So, 217 ends in 2, 218 ends in 4, 219 ends in 8.
What is units digit of 714
71 =7
72 = 49
Only the units digit will affect the next power: so we can do 9*7 =63 –> 73 ends with 3
3*7 =21 –> 74 ends with 1
1*7 = 7 –>75 ends with 7.
So, the pattern repeats for every 4 numbers in the pattern: {7, 9, 3, 1}
So, the 4th, 8th, and 12th powers would have units digit of 1.
713 has units digit of 7
714 has units digit of 9
If x and y are integers, with y > 1, how do we determine whether the fraction x/y is a repeating decimal (for example, 1/3 = .33333333… repeating), versus a “Terminating Decimal” with a finite number of digits (example: 1/40 = 0.025)?
The numerator doesn’t matter.
If the denominator only includes the prime factors 2 and/or 5, it is not repeating.
Example: 1/200 = ?
200 = 2*2*2*5*5 —> so it will be a “Terminating Decimal”
1/200 = 0.005
1/60= 3*2*2*5 = .01666666…… —> “Repeating Decimal”


