Pure Flashcards
(174 cards)
1
Q
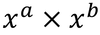
A
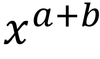
2
Q

A
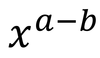
3
Q

A
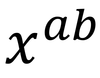
4
Q
∆
A
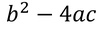
5
Q
∆ > 0
A
2 real distinct roots
6
Q
∆ = 0
A
1 repeated root
7
Q
∆ < 0
A
no real roots
8
Q
the natural numbers
A

9
Q
the integers
A

10
Q
the rationals
A

11
Q
the real numbers
A

12
Q
A is a subset of B
A
A ⊂ B
13
Q
0 < x ≤ 10 in interval notation
A
(0,10]
14
Q
The set of integers between 1 and 100 inclusive
A
{1,2,3,…,100}
15
Q
Is a member of
A
∈
16
Q
The number of members in set A is 5
A
n(A) = 5
17
Q
Universal set
A
ξ
18
Q
Complement of A
A
A’
19
Q
Union of A and B
A
A ∪ B
20
Q
Empty set
A
Ø
21
Q
A is not a subset of B
A
A ∉ B
22
Q
x is a real number and is less than 10
A
{x ∣ x∈N, x<10}
23
Q
Modulus function
A
∣x∣
24
Q
one-one
A
if every y value corresponds to only one x value
25
many-one
if there is at least one y value that comes from more than one x value
26
domain
the set of allowed input values to a function
27
range
the set of all possible outputs of a function
28
one-many
if there is at least one x value that gives more than one y value
29
a mapping is a function if...
every input value maps to a single output value
30
how can you test whether a mapping is a function?
use the vertical line test
31
mapping
takes numbers from a given set and assigns each of them one or more output values
32
image
the output of a given input
33
y = f(x) + c
translation c units up
34
y = f(x+d)
Translation d units to the left
35
y = af(x)
Vertical stretch by scale factor a
36
y = f(ax)
Horizatal stretch by 1/a
37
y = -f(x)
reflection in the x-axis
38
y = f(-x)
reflection in the y-axis
39
order of operation for vertical transformations (e.g. y = af(x) +c)
normal order of operations
40
order of operations for horizontal transformations (e.g. y = f(ax + c))
reverse of normal order of operations
41
order of operations for one horizontal and one vertical transformations (e.g. y = f(ax) + b)
doesn't matter
42
equation of a straight line
y = mx + c
43
gradient of normal
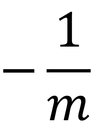
44
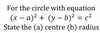
(a) (a,b)
(b) c
45
If the hypotenuse of a triangle within a circle is the diameter...
It is a right angled triangle
46
the radius of a circle at a given point on its circumference is...
perpendicular to the tangent to the circle at that point
47
increasing sequence
a sequence where each term is larger than the previous one
48
decreasing sequence
a sequence where each term is smaller than the previous one
49
periodic sequence
one where the terms start repeating after a while
50
finite sequence
has a finite number of terms
51
infinite sequence
continues forever (infinite number of terms)
52
term-to-term rule
e.g.
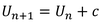
53
position-to-term rule
formula for the nth term
e.g.
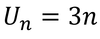
54
converge
tend to a certain value as n increases
55
diverge
increase/decrease without limit
56
series
the sum of a sequence up to a certain point (S(n))
57
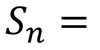
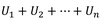
58
Write S(n) in sigma notation
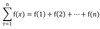
59
arithmetic sequences
sequences in which there is a common difference between each term (e.g. +4)
60
the nth term of an arithmetic sequence =
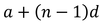
61
sum of the first n terms for an arithmetic sequence (a & d) =

62
geometric sequence
a sequence in which there is a common ration between each term (e.g. x2)
63
the nth term of a geometric sequence =
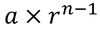
64
sequence notation - what does a mean?
the first term
65
sequence notation - what does d mean?
the common difference
66
sum of the first n terms for a geometric sequence =
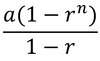
67
sequence notation - what does r mean?
common ratio
68
sum to infinity of a geometric series
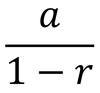
69
under what conditions does the sum to infinity condition apply?
|r| \< 1 (series converges)
70
if |r| \> 1 ...
the geometric series diverges
71
sequence notation - what does L mean?
the last term in a sequence
72
sum of the first n terms for an arithmetic sequence (a & L) =

73


74


75


76


77

0 (for any base a\>0)
78

1 (for any base a\>0)
79
Direction of a vector
The angle the vector makes with the horizontal
80
Displacement vector
The vector representing the translation from one point to another
81
Direct proportion
A relationship between two variables in which their quotient is constant
82
Congruent expressions
Expressions connected by an identity symbol (they are equal for all values of the variable)
83
Coefficient
A constant in front of a variable
84
Collinear
Points that lie along the same straight line
85
Chord
The line segment between two points on a curve
86
Exponential decay
A relationship of the form y=e-x
87
Exponential equation
An equation with the 'unknown' variable in the power
88
Exponential growth
A relationship of the form y=ex, where a\>1
89
Factorial
The product of integers from 1 to n, denoted by n!
90
Identity
A relation which is true for all values of the unknown
91
Interval notation
A form of notation to represent all numbers in a range - uses () if point is not included and [] if it is
92
Inverse proportion
A relationship between two variables in which their product is constant
93
Lead coefficient
The coefficient of the highest degree term in a polynomial
94

a \< x \< b
95

'P implies Q' or 'If P is true then Q is true'
96

'P is equivalent to Q' or 'Q is true is and only if P is true'
97
What is the degree of a polynomial?
The highest power of the unknown (x) occuring in the function
98
For a quadratic function how many...
(a) x-intercepts
(b) turning points
(a) 0-2
(b) 1
99
For a cubic function how many...
(a) x-intercepts
(b) turning points
(a) 1-3
(b) 0 or 2
100
For a quartic function how many...
(a) x-intercepts
(b) turning points
(a) 0-4
(b) 1 or 3
101


102


103
Direct proportion
Ratio of the two quantities is constant
104
What is the relationship between y and x2 if they are directly proportional?

105
What is the relationship between y and x2 if they are inversely proportional?

106
What are the 3 key circle angle rules?
1) The angle in a semi circle is a right angle
2) A tangeant to the circle is perprendicular to the radius at the point of contact
3) The radios perpendicular to the chord bisects the chord
107
What is the distance between the points (x1, y1) and (x2, y2)?

108
How can you tell whether two circles intersect, are disjoint ot tangeant to each other?
Compare the difference of the radii of the circles to the distancce betweeen their centres
109
What is *a=bc* in log form?
*c=logba*
110
Taking a logorithm of which numbers produce non-real numbers?
A negative number or zero
111
What is *log10x* written as?
*log x*
112
What is *logex* written as?
*ln x*
113
*loga(ax)*
*x*
114

x
115
What is true of all graphs of the form *y = ax* ?
1) The y-intercept is (0,1)
2) The graph of the function lies entirely above the x-axis
3) The x-axis is an asymptote
116
What is the gradient of *ex* ?
*ex*
117
What is the gradiant of *e*kx ?
*k ekx*
118
Graph of *y = ln(x)*

119
What is true of the graph *y = ln(x)* ?
1) Passes through the point (0,1)
2) The y-axis is a vertical asymptote
120
What is true of the function of the form *y = Aekt* ?
1) The initial value (when t=0) is A
2) The rate of change is ky
121
If *y = kbx* then...
*log y = log k + x log b*
122
For equation log y = log k + x log b, the graph of log y against x is a straight line with what
(a) gradient?
(b) y-intercept?
(a) log b
(b) log k
123
2 key angle identities
1) tan x = sin x / cos x
2) sin2 x + cos2 x = 1
124
Sine rule

125
Cosine rule

126
What do you have to look out for when using the sine rule?
There may be two possible answers (A and 180-A)
127
Area of a triangle

128
What is true if vectors **a** and **b** are parallel?
**b** = t**a**
129
Unit vector
A vector with magnitude 1
130
Position vector
Gives the vector from the origin to that point (its coordinates)
131
How can vectors be used to prove geometric shapes?
1) If a shape is a parallelogram then the vectors corresponding to the opposite sides are equal
2) If a shape is a rhombus then the vectors corresponding to all four sides have equal magnitudes
132
The midpoint of a line joining points with position vectors **a** and **b** had position vector...
1/2 (**a** + **b**)
133
How can the compisite function applying g to x and then f be written?

134
How is the inverse of a function written?

135
How do you write the derivative of a function?
f'(x)
136
How does the graph of y=f-1(x) relate to y=f(x)?
y=f-1(x) is a reflection of the graph y=f-(x) in the line y=x
137
What can you say about the range domain of f-1(x) and f(x)?
1) The domaine of f-1(x) is the same as the range of f(x)
2) The range of f-1(x) is the same as the domain of f(x)
138
What order are the transformations done for the function y = p f(x) + c ?
Stretch is performed before the translation
139
What order are the transformations done for the function y = f(qx + d) ?
The translation is performed before the stretch
140
Rational function
A fraction where both the denominator and numerator are polynomials
141
What is the relationship between degrees and radians?
180° = π radians
142
143
144
Converting from degrees to radians
Divide by 180º and multiply by π
145
Converting from radians to degrees
Divide by π and multiply by 180º
146
For the function y = a sin (bx) and y = a cos (bx) what is the
(a) period
(b) amplitude
in radians?
(a) 2π/|b|
(b) a
147
For the function y = a sin (b(x+c)) + d and y = a cos (b(x+c)) what is the
(a) period
(b) amplitude
(c) central value
(d) minimum value
(e) maximum value
in radians?
(a) 2π/|b|
(b) |a|
(c) d
(d) d - |a|
(e) d + |a|
148
Arc length in radians

149
Arc length in degrees

150
Area of a sector in degrees

151
Area of a sector in radians

152
Segment on a diagram

153
Sector on a diagram

154
Double angle identity for sin

155
Double angle identity for cos

156
Double angle identity for tan

157
Compound angle identity for sin

158
Compound angle identity for cos

159
Compound angle identity for tan

160
Harmonic form

161
sec x
1/cos x
162
cosec x
1/sin x
163
cot x
1/tan x
164
Identities for reciprocal trigonometric functions
Differentiation of sinx, cosx and tanx

165
Differentiation of ln x

166
Differentiation of trigonometric functions
What is the product rule?

167
Differentiate akx

168
Differentiate cos(kx)

169
Differentiate ekx

170
Differentiate sin(kx)

171
Differentiate tan(kx)

172
Implicit differentiation

173
Which two special cases of integration by substitution should be remembered?

174
Integration by parts



