Programming Problems: Advanced Algorithms Flashcards
(25 cards)
Setting the least significant bit to zero
unsigned clear_last_bit(unsigned x) {
return x & (x - 1);
}
Lowest bit set - retain only the lowest set bit
(10100 -> 00100)
unsigned lowest_set_bit(unsigned x) {
return x & ~(x-1);
}
Counting the number of bits in a number
While the number is not zero clear the least significant bit.
Clearing least significant bit: x & (x-1)
Folding over
(Setting all bits after the MSB to 1)
x |= (x >> 1);
x |= (x >> 2);
x |= (x >> 4);
x |= (x >> 8);
x |= (x >> 16);
Isolate the highest bit
x = foldOver(x); // makes all bits 1 after the highest bit
result = x & ~(x>>1)
Rounded log2 of an integer
x = x-1 // x must be unsigned int
x = foldOver(x)
x=x+1
result = 0;
while (x!=0) {
x>>=1; result++;
}
Next power of 2 that is larger than the input
result = foldOver(x) + 1
Reverse the bits in a 32bit integer
(using O(logn) time complexity)
x = ((x & 0xffff0000) >> 16) | ((x & 0x0000ffff) << 16);
x = ((x & 0xff00ff00) >> 8) | ((x & 0x00ff00ff) << 8);
x = ((x & 0xf0f0f0f0) >> 4) | ((x & 0x0f0f0f0f) << 4);
x = ((x & 0xcccccccc) >> 2) | ((x & 0x33333333) << 2);
x = ((x & 0xaaaaaaaa) >> 1) | ((x & 0x55555555) << 1);
return x;
Int multiplication using bitwise operators
int multiply(int x, int y) {
int product = 0;
while (y) {
product += x << log_x(lowest_set_bit(y));
y = clear_last_bit(y);
}
return product;
General fibonacci expression
F(0)=0; F(1)=1;
F(n)=F(n-1)+F(n-2);
Recursive fibonacci algorithm
if (n==0) return 0;
if (n==1) return 1;
return fib(n-1)+fib(n-2);
What is the runtime of the reecursive fibonacci algorithm?
Exponential function of the input.
Iterative fibonacci algorithm
if (n==0) return 0; if (n==1) return 1;
int cur = 0; int trailing = 1;
for (int i=0;i<n></n>
<p> int temp = cur;</p>
<p> cur = cur + trailing;</p>
<p> trailing = temp;}</p>
<p>return cur;</p>
</n>
Fibonacci with tail recursion
int fiboTail(int n, int fib1, int fib2) {
if (1==n) return fib1;
return fibTail(n-1,fib2,fib1+fib2);
}
int fibo(int n) {
if (0==n) return 0;
return fiboTail(n,0,1);
}
Closed formula for calculating the nth fibonacci element
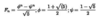
Optimized naive prime testing
- Check if the number is 0,1 or divisible by 2 –> return immediately
- Iterate from 3 to sqrt(n) by 2 and try to divide n
Eratosthene prime algorithm
- Make a boolean array of size sqrt(n)
- i = 2 to sqrt(n)
- If i is prime
- if i divides n –> return true
- j = 2*i to sqrt(n) by i: mark j not prime
- If i is prime
Add arithmetic operators to make the following expression true: 3 1 3 6 = 8. You can use any parentheses you’d like.
((3 + 1)/(3/6)=8
Write a function that swaps two numbers without using a temporary variable.
a = a^b;
b=a^b;
a=a^b;
Find the max of a and b without using comparision operators
int c = a - b;
int k = (c >> 31) & 0x1;
int max = a - k * c;
return max;
How do you know from the binary representation of a number that it is negative?
The MSB is set to 1 (if it is an int then the 32th bit is 0)
How do you multiply number by -1 using bitwise operators?
(in 2’s complement representation)
- Use binary NOT operator first (invert the bits)
- Add 1 to the result
For example: 5 = 0000 0101 –> -5 = 1111 1010 + 1 = 1111 1011
Algorithm to calculate the approximate square of an integer.
Use a binary search algorithm.
Check if the square of the middle of the current range is larger, equal or less than the original number. Alter the range accordingly or stop. Stop also when the upper range is not larger than the lower range.
SQRT for decimals is similar, but alter the stop condition, so that stop, when the range is smaller than a given delta.
How would you look for the nearest coordinate in a plane given a list of points?
Using a k-d tree with 2 dimensions.


