Problem Solving Practice

Question 1

Ratios & Proportions: The Basic Ratio Box

Answer 1

Ratios & Proportions: The Basic Ratio Box

Use the ratio box when there is a ratio and a real number in the problem.
The ratio box translates from ratios to real numbers.
Set up the ratio box like so: There are always three columns in the following order Ratio, Multiplier, Real. Rows are the parts of the ratio that appear in the problem, always followed by the Total row.

You need numbers at the Ratio column and at the Real column to figure out the multiplier.
The multiplier is applicable for all parts of the ratio box. Once you have it you can get any piece of information the question asks about.

Question 2

zA student committee that must consist of 5 members is to be formed from a pool of 8 candidates. How many different committees are possible?

5
8
40
56
336

Answer 2

To find the total number of possible committees, we need to determine the number of different five-person groups that can be formed from a pool of 8 candidates. We will use the anagram method to solve this combinations question. First, let’s create an anagram grid and assign 8 letters in the first row, with each letter representing one of the candidates. In the second row, 5 of the candidates get assigned a Y to signify that they were chosen for a committee; the remaining 3 candidates get an N, to signify that they were not chosen:

The total number of possible five-person committees that can be created from a group of 8 candidates will be equal to the number of possible anagrams that can be formed from the word YYYYYNNN = 8! / (5!3!) = 56. Therefore, there are a total of 56 possible committees.

The correct answer is D.

Question 3

Answer 3

Question 4

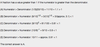
Joan, Kylie, Lillian, and Miriam all celebrate their birthdays today. Joan is 2 years younger than Kylie, Kylie is 3 years older than Lillian, and Miriam is one year older than Joan. Which of the following could be the combined age of all four women today?
51
52
53
54
55

Answer 4

It may be easiest to represent the ages of Joan, Kylie, Lillian and Miriam (J, K, L and M) on a number line. If we do so, we will see that the ages represent consecutive integers as shown in the diagram.

Since the ages are consecutive integers, they can all be expressed in terms of L: L, L + 1,
L + 2, L + 3. The sum of the four ages then would be 4L + 6. Since L must be an integer (it’s Lillian’s age), the expression 4L + 6 describes a number that is two more than a multiple of 4:

4L + 6 = (4L + 4) + 2
[4L + 4 describes a multiple of 4, since it can be factored into 4(L + 1) or 4 * an integer.]

54 is the only number in the answer choices that is two more than a multiple of 4 (namely, 52).

The correct answer is D.

Question 5

Of the films Empty Set Studios released last year, 60% were comedies and the rest were horror films. 75% of the comedies were profitable, but 75% of the horror moves were unprofitable. If the studio made a total of 40 films, and broke even on none of them, how many of their films were profitable?

18
19
20
21
22

Answer 5

Question 6

asdf

Answer 6

asdf

Question 7

Answer 7

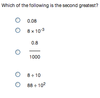
The largest number has the largest power of 10 (10-1) and the largest multiplier (8.8). The second largest number in this case has the same power of ten (10-1) and a smaller multiplier (8); this number is answer choice D.

Answer choice D is correct.

Question 8

Answer 8

Question 9

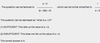
Which of the following would result in a remainder of 7 when divided by 12?

I. 151

II. 3,443

III. 5,995

I only
I and II
I and III
II and III
I, II and III

Answer 9

In order to determine whether the given dividend would result in a remainder of 7, the dividend minus 7 must equal a multiple of 12. Determining whether an integer is divisible by 12 can be determined by simple long division.

Alternatively, an integer must be divisible by 12 if it is divisible by both 3 and 4. An integer is divisible by 3 if the sum of its digits is a multiple of 3, and is divisible by 4 if the digits in its tens and ones place form a two-digit number that is divisible by 4.

I. TRUE: 151 - 7 = 144. 44 is divisible by 4, and the sum of the digits of 144 is 9, which is divisible by 3.

II. FALSE: 3,443 - 7 = 3,436. Because 36 is divisible by 4, the number 3,436 must also be divisible by 4. However, the sum of digits of 3,436 is 16, and 16 is not divisible by 3.

III. TRUE: 5,995 - 7 = 5,988. 88 is divisible by 4, and the sum of the digits of 5,988 is 30, which is divisible by 3.

The correct answer is C.

Question 10

Answer 10

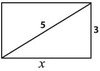
If the square has an area of 9 square inches, it must have sides of 3 inches each. Therefore, sides AD and BC have lengths of 3 inches each. These sides are lengthened to x inches, while the other two remain at 3 inches. This gives us a rectangle with two opposite sides of length x and two opposite sides of length 3. Then we are asked by how much the two lengthened sides were extended. In other words, what is the value of x – 3? In order to answer this, we need to find the value of x itself.

(1) SUFFICIENT: If the resulting rectangle has a diagonal of 5 inches, we end up with the following:

We can now see that we have a 3-4-5 right triangle, since we have a leg of 3 and a hypotenuse (the diagonal) of 5. The missing leg (in this case, x) must equal 4. Therefore, the two sides were each extended by 4 – 3 = 1 inch.

(2) INSUFFICIENT: It will be possible, no matter what the value of x, to divide the resulting rectangle into three smaller rectangles of equal size. For example, if x = 4, then the area of the rectangle is 12 and we can have three rectangles with an area of 4 each. If x = 5, then the area of the rectangle is 15 and we can have three rectangles with an area of 5 each. So it is not possible to know the value of x from this statement.

The correct answer is A.

Question 11

Set S includes elements {8, 2, 11, x, 3, y} and has a mean of 7 and a median of 5.5. If x < y, then which of the following is the maximum possible value of x?

0

1

2

3

4

Answer 11

To find the maximum possible value of x, we’ll first consider that the set’s mean is 7, and then that its median is 5.5.

For any set, the sum of the elements equals the mean times the number of elements. In this case, the mean is 7 and the number of elements is 6, so the sum of the elements equals 42.

42 = 8 + 2 + 11 + x + 3 + y
42 = 24 + x + y
18 = x + y

Now consider that the median is 5.5. Letting x = 1 and y = 17 such that they sum to 18, we can arrange the values in increasing order as follows:

x, 2, 3, 8, 11, y

Since 3 and 8 are the middle values, the median equals 5.5 as required. The question asks for the maximal value of x, so let’s increase x as far as possible without changing the median. As x increases to 3 (and y decreases to 15), the middle values of 3 and 8 don’t change, so the median remains at 5.5. However, as x increases beyond 3, the median also increases, so the maximal value of x that leaves the median at 5.5 is 3.

The correct answer is D.

Question 12

asdfasdf

Answer 12

asdfasdf

Question 13

Answer 13

Question 14

What is the distance between Harry’s home and his office?

(1) Harry’s average speed on his commute to work this Monday was 30 miles per hour.
(2) If Harry’s average speed on his commute to work this Monday had been twice as fast, his trip would have been 15 minutes shorter.

Answer 14

Distance = Rate × Time, or D = RT.

(1) INSUFFICIENT: This statement tells us Harry’s rate, 30 mph. This is not enough to calculate the distance from his home to his office, since we don’t know anything about the time required for his commute.
D = RT = (30 mph) (T)
D cannot be calculated because T is unknown.

(2) INSUFFICIENT: If Harry had traveled twice as fast, he would have gotten to work in half the time, which according to this statement would have saved him 15 minutes. Therefore, his actual commute took 30 minutes. So we learn his commute time from this statement, but don’t know anything about his actual speed.
D = RT = (R) (1/2 hour)
D cannot be calculated because R is unknown.

Question 15

Health insurance Plan A requires the insured to pay $1,000 or 50% of total cost, whichever is lower. Plan B requires the insured to pay the initial $300, but then pays 80% of the cost over $300. Which of the following is a cost level for which both insurance plans pay out the same amount?

$600
$1,000
$3,800
$5,300
$6,200

Answer 15

We can approach this problem in two ways. The first, and probably easier, method is to work backward from the answer choices and calculate how much Plans A and B pay out in each case. When the two calculated amounts are the same, we will have found our answer. For example, when the total cost is $600, Plan A requires the insured to pay $300, and the insurance plan pays the remaining $300. In contrast, Plan B requires the insured to pay the initial $300, and 20% of the excess of $600 – $300 = $300, which amounts to a total of $300 + (20%) × $300 = $360 out of the pocket of the insured. The plan pays for the remaining $240. We can see that the two amounts are not the same, so A is not our answer. We would then proceed to check the remaining answer choices in a similar manner.

An algebraic approach is the other possibility. First we need to determine how much Insurance Plan A pays. The question states that the insured pays either $1,000 or 50% of the total cost, whichever is lower. Let x be the total cost. If the insured pays $1,000, then the insurance plan pays x – 1000. If the insured pays 50% of the total cost, then the insurance plan also pays 50% of the cost, or 0.5x.

For Insurance Plan B, the insured pays the first $300, and the insurance plan pays 80% of everything over $300. So Insurance Plan B pays 0.8(x - 300).

Because there are two possible payment structures for Plan A, so we need to set up 2 equations. We are looking for the cost level for which both plans pay out the same amount, so we can set the two plans equal to each other. The two equations are:

0.8(x – 300) = x – 1,000 OR 0.8(x – 300) = .5x

Solving the first equation gives us x = 3,800, and solving the second equation gives us x = 800.

$800 isn’t one of our options, but $3,800 is.

The correct answer is C.

Question 16

Is x > y?

(1) > y
(2) x^3 > y

Answer 16

(1) AND (2) SUFFICIENT: Let’s start with statement 1 and add the constraints of statement 2. From statement 1, we see that x has to be positive since we are taking the square root of x. There is no point in testing negative values for y since a positive value for x against a negative y will always yield a yes to the question. Lastly, we should consider x values between 0 and 1 and greater than 1 because proper fractions behave different than integers with regard to exponents. When we try to come up with x and y values that fit both conditions, we must adjust the two variables so that x is always greater than y.

Logically it also makes sense that if the cube and the square root of a number are both greater than another number than the number itself must be greater than that other number.

The correct answer is C.

Question 17

If n = 10^10 and n^n = 10^d, what is the value of d?
10^3
10^10
10^11
10^20
10^100

Answer 17

Substitute the given value of n into the right-hand equation, to give

10^10*10^10

Careful with the next step! The two exponents on the left may be multiplied:

10^10*10^10

Drop the two bases and set the exponents equal to each other:
10×10^10 = d

Because the two bases are the same, you can add the two exponents:
10^11 = d

The correct answer is C.

Question 18

A scientist is studying bacteria whose cell population doubles at constant intervals, at which times each cell in the population divides simultaneously. Four hours from now, immediately after the population doubles, the scientist will destroy the entire sample. How many cells will the population contain when the bacteria is destroyed?

(1) The population just divided and, since the population divided two hours ago, the population has quadrupled, increasing by 3,750 cells.
(2) The population will double to 40,000 cells with one hour remaining until the scientist destroys the sample.

Answer 18

We need two additional pieces of information to solve this problem, which can be rephrased as “How frequently does the population double, and what is the population size at any given time immediately after it has doubled?”

(1) SUFFICIENT: If the population quadrupled during the last two hours, it doubled twice during that interval, meaning that the population doubled at 60 minute intervals. Since it has increased by 3,750 bacteria, we have:

Population (Now) – Population (2 hours ago) = 3,750
Population (Now) = 4·Population (2 hours ago)

Substituting, we get 4·Population (2 hours ago) – Population (2 hours ago) = 3,750
Population (2 hours ago) = 1,250.
The population will double 6 times from that point to 4 hours from now

Population (4 hours from now) = (26)(1,250) = 80,000.

(2) INSUFFICIENT: This statement does not give any information about how frequently the population is doubling.

The correct answer is A.

Question 19

Is x% of x% of y equal to x% less than y ?

(1) x(x + 100) = 10,000
(2) y(y + 1) = 1

Answer 19

x2y = 10,000y – 100xy [multiplying by the common denominator 10,000]

x2y + 100xy – 10,000y = 0 [everything to one side, because it’s quadratic]
y(x2 + 100x – 10,000) = 0 [factoring]
Therefore, the answer to the prompt question is affirmative if either x2 + 100x – 10,000 = 0 or y = 0.

(1) SUFFICIENT: This statement rearranges to give = 0.
(2) INSUFFICIENT: y cannot be 0, but no information is provided about x, making it impossible to determine whether x2 + 100x – 10,000 = 0.

The correct answer is A.

Question 20

What is the distance between Harry’s home and his office?

(1) Harry’s average speed on his commute to work this Monday was 30 miles per hour.
(2) If Harry’s average speed on his commute to work this Monday had been twice as fast, his trip would have been 15 minutes shorter.

Answer 20

Distance = Rate × Time, or D = RT.

(1) INSUFFICIENT: This statement tells us Harry’s rate, 30 mph. This is not enough to calculate the distance from his home to his office, since we don’t know anything about the time required for his commute.
D = RT = (30 mph) (T)
D cannot be calculated because T is unknown.

(2) INSUFFICIENT: If Harry had traveled twice as fast, he would have gotten to work in half the time, which according to this statement would have saved him 15 minutes. Therefore, his actual commute took 30 minutes. So we learn his commute time from this statement, but don’t know anything about his actual speed.
D = RT = (R) (1/2 hour)
D cannot be calculated because R is unknown.

Question 21

Health insurance Plan A requires the insured to pay $1,000 or 50% of total cost, whichever is lower. Plan B requires the insured to pay the initial $300, but then pays 80% of the cost over $300. Which of the following is a cost level for which both insurance plans pay out the same amount?

$600
$1,000
$3,800
$5,300
$6,200

Answer 21

We can approach this problem in two ways. The first, and probably easier, method is to work backward from the answer choices and calculate how much Plans A and B pay out in each case. When the two calculated amounts are the same, we will have found our answer. For example, when the total cost is $600, Plan A requires the insured to pay $300, and the insurance plan pays the remaining $300. In contrast, Plan B requires the insured to pay the initial $300, and 20% of the excess of $600 – $300 = $300, which amounts to a total of $300 + (20%) × $300 = $360 out of the pocket of the insured. The plan pays for the remaining $240. We can see that the two amounts are not the same, so A is not our answer. We would then proceed to check the remaining answer choices in a similar manner.

An algebraic approach is the other possibility. First we need to determine how much Insurance Plan A pays. The question states that the insured pays either $1,000 or 50% of the total cost, whichever is lower. Let x be the total cost. If the insured pays $1,000, then the insurance plan pays x – 1000. If the insured pays 50% of the total cost, then the insurance plan also pays 50% of the cost, or 0.5x.

For Insurance Plan B, the insured pays the first $300, and the insurance plan pays 80% of everything over $300. So Insurance Plan B pays 0.8(x - 300).

Because there are two possible payment structures for Plan A, so we need to set up 2 equations. We are looking for the cost level for which both plans pay out the same amount, so we can set the two plans equal to each other. The two equations are:

0.8(x – 300) = x – 1,000 OR 0.8(x – 300) = .5x

Solving the first equation gives us x = 3,800, and solving the second equation gives us x = 800.

$800 isn’t one of our options, but $3,800 is.

The correct answer is C.

Question 22

If a and b are negative integers, which of the following statements must be true?

I. (-a)b is positive.
II. (-a)-b is positive.
III. a-b is positive.
None
II only
I and II only
I and III only
I, II and III

Answer 22

Since a and b are negative, we know that -a and -b represent positive integers.

(I) Must be true. In this statement, -a represents a positive number and b represents a negative number. A number in the form (pos)neg is always positive because a negative exponent does not change the sign of the number. If you’re not sure, try some values: for instance, 4-2 = 1/16, 1-1 = 1, and 2-3 = 1/8.

(II) Must be true. In this statement, -a represents a positive number and -b represents a positive number. A number in the form (pos)pos is always positive. If you’re not sure, try some values: for instance, 42 = 16, 13 = 1, and 23 = 8.

(III) Does not have to be true. In this statement, a represents a negative number and -b represents a positive number. A number in the form (neg)pos can be either positive or negative, depending on whether the power is even or odd. For instance, if we plug in a = -2 and b = -2, we’ll get (-2)-(-2) = (-2)2 = 4, which is positive; however, a = -2 and b = -3 gives (-2)-(-3) = (-2)3 = -8, which is negative.

The correct answer is C.

Question 23

A certain salesman’s yearly income is determined by a base salary plus a commission on the sales he makes during the year. Was the salesman’s commission larger than his base salary last year?

(1) If the amount of the commission had been 30 percent higher, the salesman’s total income (salary plus commission) would have been 10 percent higher last year.
(2) The absolute difference between the amount of the salesman’s base salary and the amount of the commission was equal to 50 percent of the salesman’s base salary last year.

Answer 23

Let s be the salesman’s base salary, and let c be his total commission. From the question stem we can phrase the question as:

Is c > s?

(1) SUFFICIENT: The salesman’s total income is defined as s + c. This allows us to construct the following equation:
1. 1(s + c) = s + 1.3c

This gives us:
1.1s + 1.1c = s + 1.3c

0.1s = 0.2c

Therefore c is one half the size of the salesman’s base salary — and both numbers must be non-negative. This implies that the salary must account for two-thirds of the income. Thus we can answer definitively that the commission was not larger than his salary — indeed the opposite is true.

(2) INSUFFICIENT: Either s – c = .5s or c – s = .5s. We can say that one of the two is larger but we don’t know which.

The correct answer is A.

Question 24

Last year, the five employees of Company X took an average of 16 vacation days each. What was the average number of vacation days taken by the same employees this year?

(1) Three employees had a 50% increase in their number of vacation days, and two employees had a 50% decrease.
(2) Three employees had 10 more vacation days each, and two employees had 5 fewer vacation days each.

Answer 24

The average number of vacation days taken this year can be calculated by dividing the total number of vacation days by the number of employees. Since we know the total number of employees, we can rephrase the question as:

How many total vacation days did the employees of Company X take this year?

(1) INSUFFICIENT: Since we don’t know the specific details of how many vacation days each employee took the year before, we cannot determine the actual numbers that a 50% increase or a 50% decrease represent. For example, a 50% increase for someone who took 40 vacation days last year is going to affect the overall average more than the same percentage increase for someone who took only 4 days of vacation last year.
(2) SUFFICIENT: If three employees took 10 more vacation days each, and two employees took 5 fewer vacation days each, then we can calculate how the number of vacation days taken this year differs from the number taken last year:

(10 more days/employee)(3 employees) – (5 fewer days/employee)(2 employees) = 30 days – 10 days = 20 days
20 additional vacation days were taken this year.

In order to determine the total number of vacation days taken this year (i.e., in order to answer the rephrased question), we need to determine the number of vacation days taken last year. The 5 employees took an average of 16 vacation days each last year, so the total number of vacation days taken last year can be determine by taking the product of the two:

(5 employees)(16 days/employee) = 80 days
80 vacation days were taken last year.

Hence, the total number of vacation days taken this year was 100 days.

Note: It is not necessary to make the above calculations – it is simply enough to know that you have enough information in order to do so (i.e., the information given is sufficient)!

The correct answer is B.

Question 25

If #p# = ap^3+ bp – 1 where a and b are constants, and #-5# = 3, what is the value of #5#?

5
0
-2
-3
-5

Answer 25

Since we know the value of #-5# = 3, we can plug p = -5 into our formula:

(-5)3a + (-5)b – 1 = 3

  - 125a – 5b – 1 = 3
       - 125a – 5b = 4

We are asked to solve for #5#. If we plug 5 into our formula, we get:

(5)3a + (5)b – 1 = ?
125a + (5)b – 1 = ?

To figure this out, we would need to know the value of 125a + 5b.

From the first equation we know that -125a – 5b = 4. By multiplying both sides by negative one, we see that 125a + 5b = -4.

125a + 5b – 1 = ?
–4 – 1 = -5

The correct answer is E.

Question 26

Three business partners owned 100% of a certain company. When they sold the company, one partner received exactly 5/8 of the proceeds of the sale and the other partners shared the remainder of the proceeds. How much money did the partner who received the smallest amount of the proceeds receive from the sale?

(1) The partner who received the smallest amount from the sale received exactly 1/5 the amount received by the partner who received the second largest amount.
(2) The partner who received the second largest amount from the sale received half of the two million dollars received by the partner who received the largest amount.

Answer 26

We can rewrite the information in the question as an equation representing the T, the total dollar value of the sale:

L + M + S = T

L = the dollar amount received by the partner with the largest share
M = the dollar amount received by the partner with the middle (second largest) share
S = the dollar amount received by the partner with the smallest share

We are also told in the question that L = (5/8)T. Thus we can rewrite the equation as follows:

(5/8)T + M + S = T.

Since the question asks us the value of S, we can simplify the equation again as follows:

S = (3/8)T - M

Thus, in order to solve for S, we will need to determine the value of both M and T. The question can be rephrased as, what is the value of M + (3/8)T?

(1) NOT SUFFICIENT: The first statement tells us that S = (1/5)M. This gives us no information about T so statement one alone is not sufficient.
(2) SUFFICIENT: The second statement tells us that M = (1/2)L = $1 million. Additionally, since we know from the question that L = (5/8)T, then M must be equal to 1/2 of 5/8(T) or 5/16(T). We can therefore solve for T as follows:

M = $1,000,000 =
5

16
T

  $3,200,000 = T

We can now easily solve for S:

L + M + S = T
2 million + 1 million + S = $3.2 million
S = .2 million

The correct answer is B.

Question 27

What is the greatest prime factor of (36 - 1)?

2
7
11
13
17

Answer 27

We can use two methods to solve this problem. The most efficient is to factor using one of the Special Product quadratic equations. Alternatively, we can try the answer choices.

Factor
Notice that 36 is a perfect square and 1 is also a perfect square. We can use the Special Product x2 - y2 = (x + y)(x – y) to factor. 36 - 1 = (33 + 1)(33 – 1) = 26 × 28. Break these numbers down: the prime factors of 26 are 2 and 13, and the prime factors of 28 are 2 and 7. Therefore, the largest prime factor of the original quantity is 13.

Backsolve (use the answers)
We can also test for divisibility by first finding the numerical value of the quantity (36 - 1) and then performing long division using the answer choices. 36 = 3×3×3×3×3×3 = 729. 36 – 1 = 728. Once this number is obtained, divide by the numbers in the answer choices, starting with the largest choice (because the problem asks for the greatest prime factor). We’re looking for an answer that produces no remainder. Dividing 728 by 17, the largest choice, gives a quotient of 42 with 14 left over, so 17 is not the correct answer. Dividing 728 by 13, the next largest choice, gives a quotient of 56 with no remainder, so 13 is the largest prime factor of 728.

The correct answer is D.

Question 28

Is a > c?

(1) b > d
(2) ab^2 – b > b^2c – d

Answer 28

This is a multiple variable inequality problem, so you must solve it by doing algebraic manipulations on the inequalities.

(1) INSUFFICIENT: Statement (1) relates b to d, while giving us no knowledge about a and c. Therefore statement (1) is insufficient.
(2) INSUFFICIENT: Statement (2) does give a relationship between a and c, but it still depends on the values of b and d. One way to see this clearly is by realizing that only the right side of the equation contains the variable d. Perhaps ab2 – b is greater than b2c – d simply because of the magnitude of d. Therefore there is no way to draw any conclusions about the relationship between a and c.
(1) AND (2) SUFFICIENT: By adding the two inequalities from statements (1) and (2) together, we can come to the conclusion that a > c. Two inequalities can always be added together as long as the direction of the inequality signs is the same:

ab2 – b > b2c – d
(+) b > d
———————–
ab2 > b2c

Now divide both sides by b2. Since b2 is always positive, you don’t have to worry about reversing the direction of the inequality. The final result: a > c.

The correct answer is C.

Question 29

A certain store sells only black shoes and brown shoes. In a certain week, the store sold x black shoes and y brown shoes. If 2/3 of all shoes sold that week were black, which of the following expressions represents the value of y, in terms of x?

x/3
x/2
2x/3
3x/2
2x

Answer 29

We can solve this problem algebraically or we can assign values to x and y and use those numbers to determine the correct answer. Let’s try picking numbers first.

Since the question deals with thirds (2/3, to be precise), let’s choose a total number of shoes that is divisible by 3. Let’s say 6, for example. If 2/3 of the 6 shoes sold were black, this represents (2/3)(6) = 4 shoes. This leaves 2 brown shoes to make up the difference. The question asks which of the given expressions represents the value of y (the number of brown shoes sold). Since y = 2 in our example, all we have to do is plug 4 (the value of x) into all of the expressions and see which yields 2 as a result:

(A) 4/3 = 1.33 Incorrect
(B) 4/2 = 2 CORRECT
(C) 2(4)/3 = 8/3 = 2.33 Incorrect
(D) 3(4)/2 = 12/2 = 6 Incorrect
(E) 2(4) = 8 Incorrect

Alternatively, we can solve this algebraically:

Since x is 2/3 of the total number of shoes, we can express this as

x = (2/3)(x + y)
x = (2x + 2y)/3
3x = 2x + 2y
x = 2y
x/2 = y

The correct answer is B.

Question 30

Peter, Paul, and Mary each received a passing score on his/her history midterm. The average (arithmetic mean) of the three scores was 78. What was the median of the three scores?

(1) Peter scored a 73 on his exam.
(2) Mary scored a 78 on her exam.

Answer 30

This question is asking us to find the median of the three scores. It may seem that the only way to do this is to find the value of each of the three scores, with the middle value taken as the median. Using both statements, we would have two of the three scores, along with the mean given in the question, so we would be able to find the value of the third score. It would seem then that the answer is C. On GMAT data sufficiency, always be suspicious, however, of such an obvious C. In such cases, one or both of the statements is often sufficient.

(1) INSUFFICIENT: With an arithmetic mean of 78, the sum of the three scores is 3 × 78 = 234. If Peter scored 73, the other two scores must sum to 234 – 73 = 161. We could come up with hundreds of sets of scores that fit these conditions and that have different medians. An example of just two sets are:
73, 80, 81 median = 80
61, 73, 100 median = 73

(2) SUFFICIENT: On the surface, this statement seems parallel to statement (1) and should therefore also be insufficient. However, we aren’t just given one of the three scores in this statement. We are given a score with a value that is THE SAME AS THE MEAN.

Conceptually, the mean is the point where the deviations of all the data net zero. This means that the sum of the differences from the mean to each of the points of data must net to zero. For a simple example, consider 11, which is the mean of 7, 10 and 16.
7 – 11 = -4 (defined as negative because it is left of the mean on the number line)
10 – 11 = -1
16 – 11 = +5 (defined as positive because it is right of the mean on the number line)
The positive and negative deviations (differences from the mean) net to zero.

In the question, we are told that the mean score is 78 and that Mary scored a 78. Mary’s deviation then is 78 – 78 = 0. For the deviations to net to zero, Peter and Paul’s deviations must be -x and +x (not necessarily in that order).

Mary’s deviation = 78 – 78 = 0
Peter’s (or Paul’s) deviation = -x
Paul’s (or Peter’s) deviation = +x

We can then list the data in order: 78 – x, 78, 78 + x
This means that the median must be 78.
NOTE: x could be 0, which would simply mean that all three students scored a 78. However, the median would remain 78.

The correct answer is B.

Question 31

If the sum of the cubes of a and b is 8 and a6 – b6 = 14, what is the value of a3?

7/4
23/6
39/8
6
22/3

Answer 31

We know that the sum of the cubes of a and b is 8: a3 + b3 = 8. We also know that a6 – b6 = 14. Using our knowledge of the quadratic template for the difference of two squares,
x2 – y2 = (x + y)(x – y), we can rewrite a6 – b6 = 14 as follows:

(a3)2 – (b3)2 = 14
(a3 – b3)(a3 + b3) = 14

Substituting for a3 + b3 gives:

(a3 – b3)(8) = 14
(a3 – b3) = 14/8 = 7/4

Now that we have a value for a3 + b3 and a value for a3 – b3, we can solve for the value of a3 using elimination.

a3 + b3 = 8
a3 – b3 = 7/4

2a3 = 39/4
Divide both sides by 2, and a3 = 39/8.

The correct answer is C.

Question 32

John’s front lawn is 1/3 the size of his back lawn. If John mows 1/2 of his front lawn and 2/3 of his back lawn, what fraction of his lawn is left unmowed?

1/6

1/3

3/8

1/2

5/8

Answer 32

Front lawn: (1/2)(2) = 1 unit
Back lawn: (2/3)(6) = 4 unit

So, in total, 5 units of lawn have been mowed. This represents 5/8 of the total, meaning 3/8 of the lawn is left unmowed.

Alternatively, this problem can be solved using an algebraic approach. Let’s assume the size of the front lawn is x and size of the back lawn is y. So, John has mowed (1/2)x and (2/3)y, for a total of (1/2)x + (2/3)y. We also know that x = (1/3)y. Substituting for x gives:

(1/2)x + (2/3)y
(1/2)(1/3)y + (2/3)y
(1/6)y + (2/3)y
(5/6)y = lawn mowed

The total lawn is the sum of the front and back, x + y. Again, substituting for x gives (1/3)y + y = (4/3)y. So, the fraction of the total lawn mowed is:

lawn mowed

total lawn

(5/6)y

(4/3)y
=
(5/6)

(4/3)
= (5/6) × (3/4) = 15/24 = 5/8. This leaves 3/8 unmowed.

The correct answer is C.

Question 33

If 10y/(2^m) is an odd integer, then y may be which of the following?

2^m
2^m+1
2^m−1
(2^m)/5
5×(2^m)

Answer 33

Correct.

Plug in C: replace y with 2m-1 to get

10y / (2m) =

–> 10(2m-1) / (2m) =

Combine all the 2s under the same power. There’s another 2 hiding in the 10, so split the 10 into 5⋅2:

–> 5⋅2⋅(2m-1) / (2m)

Using the rules of multiplying powers with the same base, 2⋅2m-1becomes 2m-1+1 = 2m =

5(2m) / (2m)

= 5.

Since 5 is odd, this is the correct answer.

Question 35

Answer 35

C

Question 36

If m=√(m/6), which of the following could be the value of m?

1/6
6
36
63
64

Answer 36

Correct.

Square both sides of m=√(m/6)

i.e. m2= (√(m/6))2

Focus on the right side of the equation: Powers and roots of the same order cancel each other. Delete the power of 2 and the square root √, and (√(m/6))2 simply becomes m/6.

–> m2= (m/6)

Now divide both sides of the equation by m to get

–> m= (1/6)

The other solution for the above quadratic equation (m=0) is not one of the answer choices. Hence, this is the correct answer.