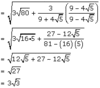
Fractions Flashcards
(7 cards)
Fractions: Reciprocal
The reciprocal or the inverse of a fraction is that fraction flipped over; top to bottom and bottom to top. i.e., the reciprocal of 2/5 is 5/2.
Remember that the reciprocal doesn’t change signs.
To find the reciprocal of an integer, write it in fraction form first, then flip. i.e. 5 can be written as 5/1, hence the reciprocal is 1/5.
Fractions: Multiplying
To multiply fractions, multiply straight across, tops with tops, bottoms with bottoms.
If possible reduce before you multiply.
When multiplying a fraction and an integer, first write the integer as a fraction, then multiply.
Fractions - Denominator Dynamics - increase the denominator
The greater the denominator, the smaller the fraction (under the same numerator).
e.g. 1/2 > 1/3 > 1/4
The reverse is also true:
The smaller the denominator, the greater the fraction (under the same numerator).
e.g. 1/10 < 1/5 < 1/2 < 1/(1/2) = 2/1
Which of the following fractions is at least twice greater than 11/50?
2/5
11/34
43/99
8/21
9/20
First, let us rephrase the question. Since we need to find the fraction that is at least twice greater than 11/50, we are looking for a fraction that is equal to or greater than 22/50. Further, to facilitate our analysis, note that we can come up with an easy benchmark value for this fraction by doubling both the numerator and the denominator and thus expressing it as a percent: 22/50 = 44/100 = 44%. Thus, we can rephrase the question: “Which of the following is greater than or equal to 44%?”
Now, let’s analyze each of the fractions in the answer choices using benchmark values:
2/5: This fraction can be represented as 40%, which is less than 44%.
11/34: This value is slightly less than 11/33 or 1/3. Therefore, it is smaller than 44%.
43/99: Note that the fraction 43/99 is smaller than 44/100, since fractions get smaller if the same number (in this case integer 1) is subtracted from both the numerator and the denominator.
8/21: We know that 8/21 is a little less than 8/20 or 2/5. Thus, 8/21 is less than 44%.
9/20: Finally, note that by multiplying the numerator and the denominator by 5, we can represent this fraction as 45/100, thus concluding that this fraction is greater than 44%.
The correct answer is E.
Lindsay can paint 1/x of a certain room in one hour. If Lindsay and Joseph, working together at their respective rates, can paint the room in one hour, what fraction of the room can Joseph paint in 20 minutes?
1/3x
x/x – 3
x – 1/3x
x/x – 1
x – 1/x
We can solve this problem as a VIC (Variable In the Answer Choices) and plug in values for the variable x. Let’s say x = 4. (Note that there is a logical restriction here in terms of the value of x. Lindsay has to have a rate of less than 1 room per hour if she needs Joseph’s help to finish in an hour). If Lindsay can paint 1/4 of the room in one hour, her rate is 1/4. This implies that Joseph can paint 3/4 of the room in one hour. At that rate, he could paint 1/4 of the room in 20 minutes.
Only C equals 1/4 when you plug in 4 as a value for x: (4 - 1) / (3 x 4) = 1/4.
The correct answer is C.
As an alternative, you could take a purely algebraic approach.
Together, they can paint the whole room in 1 hour (60 minutes), and so we’ll first solve for how much of the room Joseph can paint in one hour, then divide by three once we get that number.
The work Lindsay does + the work Joseph does = the total work done. Let’s say that the work Joseph does is 1/y.
Then we have this equation: 1/x + 1/y = 1
Solving for 1/y, we get 1/y = 1 - 1/x. The right-hand side of the equation simplifies to the following expression:
x – 1
x
Remember that we want to know how much work Joseph does in 20 minutes, which is 1/3 of that:
Again, the correct answer is C.