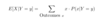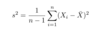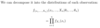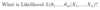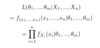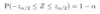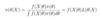Probability and Statistics Basics

Question 1

Prob: What are the two equivalent definitions of events A and B being independent?

Answer 1

P(A,B) = P(A)P(B)

OR

P(A) = P(A | B=b) for all values of b

(Pretty darn sure second is correct)

Question 2

Prob: What are the two equivalent definitions of random variables Y1 and Y2 independent?

Answer 2

F(y1,y2) = F1(y1)F2(y2) (The joint dist factors to the marginal dists)

OR

F1(y1) = F(y1 | Y2 = y2) for all values of y2 (The marginal distribution for either variable is the same as the conditional distribution given any value of the other variable)

(Pretty darn sure second is correct)

Question 3

Prob: Conceptually, what does it mean for A and B to be independent, either as variables or as events?

Answer 3

A and B are independent variables if the value of one variable gives you no information about the value of the other.

A and B are independent events if knowing whether one event happened or not gives you no information on whether the other happened.

Question 4

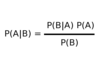
Prob: What is Bayes’ Theorem?

Answer 4

Question 5

Prob: What is a formula for P(A union B)?

Answer 5

P(A) + P(B) - P(A and B)

Question 6

Prob: What is linearity of expectation?

Answer 6

E[cX + kY] = cE[X] + kE[Y], even if X and Y are dependent

Question 7

Prob: What is one potentially convenient way to find P(A and B) when A and B are dependant?

Answer 7

P(A)*P(B|A), or P(B)*P(A|B)

Question 8

Stat: What proportion of points drawn from a normal distribution will fall within 1 standard deviation? 2? 3?

Answer 8

68% within 1, 95% within 2, 99.7% within 3

Question 9

Prob: What is the law of total probability?

Answer 9

If you can decompose the sample space S into n parts B1,…,Bn, then

P(A) = P(A|B1)P(B1) + … + P(A|Bn)P(Bn)

A common form is

P(A) = P(A|B)P(B) + P(A|B^c)P(B^c)

Question 10

Prob: What trick is often used in the denominator of a Bayes’ Rule problem?

Answer 10

Law of total probability

Question 11

Prob: What is a probability density function, or pdf f(), typically used for?

Answer 11

For a given probability distribution, you can integrate f() over an interval (or area, or n-d area) to find the probability that an experiment will fall in that interval/area.

Question 12

Prob: what is a cumulative density function F(), or cdf, typically used for? How is it related to the pdf f()?

Answer 12

For a given probability distribution of RV X, F(x) = P(X <= x)

If you integrate f() from -inf to a, you get F(a)

Question 13

Prob: What is the formula for the expected value of discrete RV X?

Answer 13

Question 14

Prob: What is the formula for E[g(X)], or the expected value of a function g of continuous RV X, with pdf f()?

Answer 14

Question 15

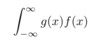
Prob: V[aX+b]?

Answer 15

a²V[X]

Question 16

Prob: Conceptually, what does it mean for a probability distribution Y to be memoryless?

Answer 16

For an experiment, past behavior has no bearing on future behavior. For example, if you’re waiting for a bus to come and it follows a memoryless distribution (such as an exponential one), if you wait 5 minutes and there’s still no bus, the probability distribution of when it will arrive starting now, after 5 minutes is the same as it was when the experiment began.

Question 17

Prob: what is the expected value of a geometric random variable (i.e. flip coin until a success) with probability p of success?

Answer 17

1/p

Question 18

Prob: If our binonial distribution (flip n times, see how many are succcesses) has events with probability p of success, and we conduct n events, what is the probability that y will be successes (assuming 0 <= y <= n)? And what is the intuition behind this result?

Answer 18

p^y(1-p)^n-y is the odds of a specific result with y successes (so y specific positions being successes, and the other n-y being failures). But we need the probability of any; these occurrences are disjoint, so we sum their probabilities by multiplying by the number of such potential outcomes, which is n choose y.

Question 19

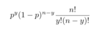
Prob: In words, what is the law of large numbers?

Answer 19

When sampling from a distribution, as the number of samples grows, the sampling mean will tend towards the expected value of the distribution.

Question 20

Normal: If Y follows N(µ,ð²), what is the formula for the z-score Z of Y=y?

Answer 20

Z = (y - µ)/ð

Question 21

Normal: If Y follows N(µ,ð²), what (in words) is the z-score of Y=y?

Answer 21

The number of standard deviations ð that y is above or below the mean µ.

Question 22

Stat: What does the standard normal distribution Z follow?

Answer 22

Z follows N(0,1)

Question 23

Prob: What is the law of total expectation?

Answer 23

We can find E[X] by taking the weighted sum of the conditional expectations of X given all values of a variable Y.

For example, if Y = Y₁ or Y₂, then

E[X] = E[X|Y₁]P(Y₁) + E[X|Y₂]P(Y₂)

Question 24

Prob: What is the formula for the conditional expectation of X given that Y=y?

Answer 24

Question 25

Answer 25

Question 26

Stat: What is our estimator Ø_h (theta-hat) a function of?

Answer 26

The data X1, X2, X3…! (This is important!)

Question 27

Stat: Given what our estimator Ø_h is a function of, what 2 important properties does it have?

Answer 27

It is a random variable

Which means it has its own probability distribution, with E[Ø_h], V[Ø_h], etc

Question 28

Stat: What, in these flashcards, is my notation for Theta and Thet-hat?

Answer 28

Ø and Ø_h respectively.

Question 29

Stat: At a high level (so like coloquially explaining the formula), how do you find the sample variance s² given data X1,…,Xn?

Answer 29

Question 30

Stat: What does it mean for an estimator Ø_h to be accurate?

Answer 30

It has a mean close to the true value Ø; in other words, its bias is low.

Question 31

Stat: What does it mean for an estimator Ø_h to be precise?

Answer 31

It tends to produce similar answers each time; in other words, its variance is low.

Question 32

Stat: What is the formula for MSE(Ø_h), or Mean Squared Error?

Answer 32

MSE(Ø_h) = E[(Ø_h - Ø)² ]

= V(Ø_h) + bias(Ø_h)²

but only really need that first part

Question 33

Stat: What is the formula for the bias of Ø_h? What does it mean for Ø_h to be unbiased?

Answer 33

Bias(Ø_h) = E[Ø_h - Ø]

Ø_h is unbiased iff Bias(Ø_h) = 0, or if the expected value of Ø_h is the correct value Ø.

Question 34

Stat: What is the standard error of Ø_h? And what in general does this quantity represent?

Answer 34

SE(Ø_h) = sqrt(V[Ø_h])

It is an idea of the typical error of the estimator, or the typical distance it will be from its mean.

Question 35

Answer 35

Question 36

Stat: What is probably the most common measure of the quality of estimator Ø_h?

Answer 36

Mean Squared Error, or MSE(Ø_h)

Question 37

Answer 37

It describes how likely those a distribution with those parameters was to make that dataset.

(I think it is often talked about in the context of a specific family of distributions. So we might say, what is the likelihood of a normal distribution with these paramaters, given this dataset?)

Question 38

Answer 38

Question 39

Stat: What does i.i.d. stand for?

Answer 39

Independent and Identically Distributed

Question 40

Stat: What is a MVUE?

Answer 40

It’s a Minimim-Variance Unbiased Estimator. So for some parameter Ø, it’s the unbiased estimator Ø_h with the lowest variance out of all the unbiased estimators.

Question 41

Stat: When we find a Maximum Likelihood Estimator, Min-Var Unbiased Estimator, Method of Moments Estimator, or something similar, do we typically find it in the context of some assumed distribution family (i.e. assume the distribution is normal, exponential, etc), or estimate parameters without a suspected distribution?

Answer 41

While sometimes we estimate parameters without a suspected distribution, such as distribution mean and variance, we generally more often use an assumed distribution family.

(This is mostly my opinion, and also me wanting to remember that when we for example “find the MLE”, it generally has quite a bit of structure due to an assumed distribution that we can differentiate/optimize.)

Question 42

Stat: What is a Maximum Likelihood Estimator?

Answer 42

It is the estimator Ø_hat of Ø that maximizes the likelihood of your data.

So, generally for some assumed distribution family such as Exponential Distributions, you try to find an estimator lambda_hat for parameter lambda that leads to the exponential distribution that was most likely to produce this data.

Question 43

Stat: At a high level, how do you find the MLE estimate for the parameters?

Answer 43

Differentiate the likelihood w.r.t. the parameters and set that equal to zero, then solve

Question 44

Stat: Given observations X₁,…,X_n, what is the maximum likelihood estimator for a population proportion: for example, the proportion of red balls if we’re drawing from red, green or blue?

Answer 44

reds/n

Question 45

Stat: Define a 95% confidence interval [L,U] for parameter Ø.

Answer 45

For L and U, which are random variables based on your observations X_i, P(L <= Ø <= U) = 95%.

Meaning, when you sample your X_i’s and calcuulate L and U, the odds that then end up so L <= Ø <= U is 95%.

Question 46

Stat: What is the correct way to interpret 95% confidence interval [L,U] for parameter Ø?

What is a common incorrect way of interpreting it, and why is this incorrect?

Answer 46

Correct: “I am 95% confident that my calculated confidence interval [L,U] contains Ø.”

Incorrect: “There is a 95% chance that Ø is in the interval [L,U].”

The latter is incorrect because the true population parameter Ø is not a random variable. It is a set value that just exists in the world, and it either is in the interval or it isn’t; there is no chance involved.

Question 47

Stat: What is the way of interpreting a 95% confidence interval that involves considering if you computed many 95% confidence intervals?

Answer 47

If I compute a high number of 95% confidence intervals, over time, about 95% of them will contain their respective parameters.

Question 48

Stat: Given observations X_i and an unknown parameter Ø, what is a pivot?

Answer 48

A pivot is and expression that is :

• A function of the observable R.V.’s (i.e. the observations X_i)
• And of the unknown parameter Ø,
• But no other unknowns.
• And who’s distribution does not depend on the unknown Ø.

This is an important one!

Question 49

Stat: What is the Central Limit Theorem?

Answer 49

Question 50

Stat: Why is the Central Limit Theorem so important and useful?

Answer 50

Given enough sample size, we can find an approximate distribution for the sample mean of the X_i’s, but we don’t need to know anything about the underlying distribution of X_i! It doesn’t need to be of a specific family, and it can be an insane looking distribution, but we can still find an approximate distribution of the sample mean.

Using this, we can also find a confidence interval for the sample mean, which is great.

Question 51

Stat: This varies from table to table, as some have different definitions. But in your stats class, what was the definition of z_a?

Answer 51

If Z is the standard normal N(0,1), z_a is such that

P(Z > z_a) = a

Graphically, or verbally: the probability a draw from Z appearing above z_a is a.

Question 52

Stat: Given our definition of z_a (and with similarly defined quantities like t_a,n-1 and chai-squared_a,n-1), what is the probability expression used in almost all confidence intervals we make?

Answer 52

The following, which can be similarly written for t dist, chai-squared dist, etc. But it’s especially common to use the normal version, due to the CLT and all the great info we have about normals.

Question 53

Stat: In hypothesis testing, what is a null hypothesis?

Answer 53

Null Hypothesis H_o is the “status quo” or “safe hypothesis”. It is the baseline, and we are looking for significant evidence that it is not true. For example, when testing whether two groups have different performance on a task, the null hypothesis is that their performance is the same.

Question 54

Stat: In hypothesis testing, what is an alternative hypothesis?

Answer 54

The alternative hypothesis an idea that breaks from the “status quo” or “baseline assumption”, for which we are looking to see if there is significant evidence. For example, when testing whether two groups have different performance on a task, the alternative hypothesis could be that group A performs better than group B, for example.

Question 55

Stat: In hypothesis testing, what is a test statistic?

Answer 55

The test statistic in a hypothesis test is a function of your observable data which you will use to quantitatively examine your null and alternative hypotheses. For example, when testing whether two groups have different performance on a task, the test statistic might be the difference in mean performances of the 2 groups.

Question 56

Stat: What are the 2 possible conclusions an experimenter can make from a hypothesis test?

Answer 56

“Reject the null hypothesis in favor of the alternative,” and “Fail to reject the null hypothesis.”

Question 57

Stat: In hypothesis testing, what is the rejection region?

Answer 57

It is the predecided range of (extreme) values of the test statistic in which we will “reject the null hypothesis in favor of the alternative.”

Question 58

Stat: In hypothesis testing, what is a Type 1 error?

Answer 58

It is when we reject the null hypothesis H_o even though it is true.

Question 59

Stat: In hypothesis testing, what is a Type 2 Error?

Answer 59

It is when we fail to reject the null H₀, but the alternative H₁ is true,

Question 60

Answer 60

Question 61

Stat: In hypothesis testing, what does a “level 0.05 test” mean?

Answer 61

Alpha = 0.05

Question 62

Stat: In hypothesis testing, what would a low value of alpha such as 0.001 mean? What about a high value like 0.20?

Answer 62

A low value of alpha like 0.001 means that we require very compelling evidence (or very extreme values of our test statistic) in order to reject the null hypothesis.

Conversely, a high value like 0.20 means that we have very relaxed and un-stringent requirements for rejecting our null hypothesis.

Question 63

Stat: In hypothesis testing, what is a p-value?

Answer 63

Once you conduct your experiment and calculate the test statistic, the p-value is the probability of getting results that are as extreme or more extreme than your test statistic, under the assumption that the null hypothesis is true.

Question 64

Stat: In hypothesis testing, what value do we use to determine whether or not we reject the null.

Answer 64

The p-value. (We need to calculate the p-value from the test statistic under the assumption of the null, in order to see how unlikely our result is under the null.)

Question 65

Stat: In hypothesis testing, what do we conclude if the p-value is larger than alpha?

Answer 65

If say, p-val = 0.10 and alpha = 0.05, then our results are not as extreme as our alpha requires, and so we fail to reject the null hypothesis.

Question 66

Stat: In hypothesis testing, what do we conclude if the p-value is smaller than alpha?

Answer 66

If say, p-val = 0.01 and alpha = 0.05, then our results are more extreme than our alpha requires, and so we reject the null hypothesis in favor of the alternative hypothesis.

Question 67

Stat: In hypothesis testing, what is a one-sided hypothesis?

Answer 67

We reject only if the test statistic is extreme in one of the two directions. For example, if the null is µ = 0, the alternative is µ > 0.

Question 68

Stat: In hypothesis testing, what is a two-sided hypothesis?

Answer 68

We reject if the test statistic is extreme in either directions. For example, if the null is µ = 0, the alternative is µ =/= 0, and we reject if the test statistic is extremely high or extremely low.

Question 69

Stat: What is the key feature of classical, or frequentist, statistics? And what are some types of analytical tools used in this statistical philosophy?

Answer 69

In classical/frequentist statistics, the parameter Ø is constant. We examine it using estimators Ø_h, we quantify our uncertainty of its value using confidence intervals, and we test theories using hypothesis tests and p-values.

Question 70

Stat: What is the key feature of bayesian statistics? And what are some types of analytical tools used in this statistical philosophy?

Answer 70

The parameter Ø is viewed as variable, and we quantify our opinions around its potential values using a prob dist π.

Question 71

Stats: In Bayesian statistics, how do we update π, our prior distribution of Ø, using data Xi?

Answer 71

You incorporate using a method looking very similar to Bayes’ law.

Specifically:

Question 72

Stats: In bayesian statistics, what happens to the prior distribution as we get more and more data?

Answer 72

With enough data, the impact of the prior distribution on the posterior distribution tends towards 0.