Deep Learning, xgb, BERT Flashcards
(122 cards)
1
Q
Intuitively, why should a NN/MLP with a bunch of successive layers of processing be good at finding patterns, like identifying images of digits?
A
The intuitive idea is that each subsequent layer is being trained to recognize higher-level patterns. So maybe layer 1 is edge detection, layer 2 is finding a shape like a circle, and layer 3 can identify full digits.
In a more complex image, maybe layer 1 is lines, layer 3 is texture, etc.
2
Q
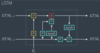
In a “vanilla NN”, or MLP, how does a given layer of processing work? How do we go from layer i of size N to layer i+1 of size M?
A
Each of the M neurons in the output layer is computed by taking a weighted sum of all the values of the input layer (plus a bias), then passing it through an activation function. Typically the weights are learned but the activation is not, it’s something like relu or sigmoid.
So in order to get one of the output neurons, you take the N inputs, plus an input of 1 that’ll be multiplied by the bias, as a column vector and multiply them by a length N+1 row vector of weights; then you take the that output and pass it through the activation.
So if you want a length M output, you need M row vectors, and thus you’re multiplying the length-N+1 input by an MxN+1 matrix to get the length M output (which goes through the activation).
3
Q
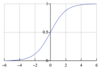
What is the sigmoid activation? What is its formula, and what does the graph look like? What does it functionally “do”?
A
It squishes all the real numbers between 0 and 1, like in logistic regression.
4
Q
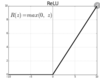
What does the relu activation function look like?
A
5
Q
What is the softmax function? How is it computed, and what is it used for?
A
The softmax is the go-to output layer if you’re predicting a categorical variable with more than 2 categories. All the layer outputs are between 0 and 1, and they sum to 1 – so they’re basically probabilities (they aren’t exactly but can often kinda be interpreted that way), and whichever outcome class is being predicted as having highest probability is chosen.
The formula is shown below, where there are K values you’re trying to predict, each has a corresponding value z that needs to be passed through the softmax.
It’s similar to sigmoid
6
Q
When learning an NN, what gradient are you calculating during optimization, and why? How does gradient descent work?
A
In order to optimize a neural network, you need to find the derivative of the loss function with respect to each of the weights in the network (maybe thousands or millions), and then you update the weights by taking a small step in that direction (I think technically the opposite direction but whatever).
If you want the partial derivative of a function with respect to each input variable, that’s the gradient: the gradient of the loss function is the vector of the function’s partial derivatives with respect to each parameter. So that’s what we calculate and optimize based on.
7
Q
Conceptually, how does backpropogation work?
A
Basically you use the chain rule to efficiently get the partial derivatives one layer at a time.
You start by setting up the formulas to get the partial derivatives of the loss function with respect to the weights in the last layer. **These formulas will depend on the activation of the previous layer**, but you just hold that value constant while simply calculating the partial derivatives of this layer.
Then, basically using the chain rule, you substitute in the formula for the activation from the previous layer, and now holding constant the stuff from the subsequent layer, you simply calculate your next round of partial derivatives.
Then repeat, because the now the formula is dependent on the activation of the previous layer, which you can again substitute in, etc! I’m not gonna get totally into the weeds memorizing the exact math.
New simple and valuable thing to remember: The chain rule is just dy/dx = dy/du*du/dx, so it makes sense that dLoss/dSecondLayer = dLoss/dFirstLayer * dFirstLayer/dSecondLayer. And that shows clearly how gradients are based on past ones, and are eventually long chains of multiplied gradients (which could lead to vanishing gradients)
8
Q
What is one-hot encoding? Why is it needed for neural networks?
A
Basically if you have a categorical variable with N>2 outputs, you’ll represent each row’s value of that variable wth N columns, each pertaining to one of the N categories. There’ll be a 1 for the category in that row, and 0s otherwise.
You need to one-hot encode because NNs need numerical inputs, so they can do computations by multiplying input vectors by weight matrices, and use derivatives of numerical formulas to optimize.
9
Q
Why is the activation function important?
A
Without a nonlinear activation, you would just be learning a bunch of complex weighted sums of the inputs; it would be all linear. Nonlinear activations let you learn nonlinear relationships, which is where the magic happens.
10
Q
How are log loss and cross entropy loss related? How do they work?
A
New:
Remember the specifics here: it’s the sum of the negatives of isCorrect*log(predictedProb) for each class.
So a term only has weight if it’s the prob for the correct label (I had misremembered it as all the other ones have weight, not that one.)
And log(1)=0, log(decimal) = big negative number. So if you predict low for the truth, you get a big negative log value, then take its negative to get a big positive loss, as desired.
I’m confident this is the case.
Original:
Log loss (also called binary cross entropy) is for a binary categorical and cross entropy is 3+ outcomes, but they’re basically the same thing; it’s like sigmoid vs softmax.
These loss functions are just using negative log likelihood. So we are trying to find the maximum likelihood estimation of the best parameters: we try to find the parameters such that “the likelihood that those parameters, and the associated probabilties they yield, would have resulted in this dataset” is maximized.
So like, when we’re predicting a categorical variable, our model’s output is a bunch of probabilities. We want to get those probabilties close to being 1 for the correct answer and 0 for everything else, because that is the maximum likelihood solution: those are the probabilties that are most likely to have yielded this label, and thus the parameters associated with that probability are most likely to yield that label.
11
Q
What’s the formula for log likelihood, aka binary cross entropy?
A
Hopefully this isn’t that important to memorize if you’ve got the concept
12
Q
What final activation is typically used, and what loss function is typically used, for predicting a binary categorical variable?
What about a categorical with 3+ options?
A
Activation is sigmoid, loss is BCE.
For 3+, activation is softmax, loss is cross entropy.
13
Q
Why is it important to normalize all of your input columns?
A
So all of the input columns have the same scale, making it easier to learn at approximately the same rate (and using the same learning rate parameter) for each input.
If one col had a really big scale and another had a really small scale, then a step that’s as large as the learning rate will be hard to get right for both columns: you might have a too-big step for the small-scale one, and vice versa.
14
Q
What is the learning rate?
When would you decrease the learning rate? When would you increase it?
A
The learning rate is a positive scalar that determines how large of a step you take in the opposite direction of the gradient each time you take a step.
You would increase it if you’re learning too slowly, and decrease it if you’re underfitting or if your learning is jagged.
15
Q
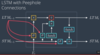
What is dropout regularization? Why does it work as a regularization tactic?
A
Dropout regularization is when we give nodes in the network a probability that they will be turned off on a training pass. So each time the model is run during training, we look at each node that might turn off, and if we pull the appropriate random number, set it to zero for this training run.
So for every training evaluation, we’re using a random subset of the nodes; the other nodes, and by extension their incoming and outgoing connections, are removed. (We don’t do dropout during validation or testing.)
My intuitive understanding of why it works for overfitting: first of all, it on average decreases the size of the model during training, and smaller/less complex models overfit less.
Also, because the model cannot consistently rely on having a specific node on a given run, it’s harder to, say, encode in one specific training point’s outcome variable in one specific node. Like if for example the model were trying to encode each training point’s individual outcome variable using one node each, that wouldn’t work super well with high dropout.
16
Q
What causes vanishing gradients in neural networks, especially deep neural networks?
A
Certain activation functions have areas where their derivatives are very near zero: for example, the extreme values of sigmoid. So if all or most of the neurons get to the extreme values of sigmoid, the gradients will have a lot of very-near-zero values, which causes very slow training.
This is exacerbated by the fact that derivatives in NNs are often basically the the product of several of these individual derivatives, chained together by the chain rule. So you’ve got a bunch of near-zero values multiplied together.
17
Q
Intuitively, why does using the relu activation function combat vanishing gradients, and exploding gradients?
A
A derivative in an NN is usually a bunch of individual derivatives of the activation function multiplied together, because of the use of the chain rule in backpropogation.
If the activation derivative tends to often be less than 1 (as with the extremes of sigmoid), these derivatives will tend to zero, and vanish. If they often to be greater than 1, they will tend to infinity and explode.
But the derivative of relu is always either zero or 1. So the product of a bunch of the derivatives will be either zero and 1, but some of them will typically be 1, because the network will need some info flowing through for each point. So there are usually always some gradients that aren’t vanishing and aren’t exploding
18
Q
How do you get the best of both worlds of normal gradient descent and stochastic gradient descent
A
Stochastic batch gradient descent: take a step every batch of k datapoints, rather than every 1, or just every epoch. Super common
19
Q
Why is learning rate decay useful?
A
Usually we want to take large steps at the beginning and slow steps at the end: at the end we’re near a local minimum and just want to slightly refine, where as at the beginning we probably have quite a ways to go.
20
Q
How does momentum work, and what purpose does it attempt to solve?
A
In momentum, rather than taking a step in the direction of the current gradient, you take a step in the direction of an exponentially decaying weighted sum of all past gradients.
The hope is that it helps you “power through” local minima to reach global minima. So for example, if you got to the bottom of this local minimum, the current gradient would be zero, but the previous ones are still pointing right and would carry you through.
Another benefit is that momentum helps decrease jagged training. If the objective function is pointing in a consistent direction in one dimension (long side of ovals below), but prone to jumping around on another one (short side of ovals below), momentum smoothes this out.
21
Q
What little optimization can often be made to the pairing of softmax output and cross entropy loss?
A
Rather than having softmax output probabilities, have it output the logs of the probabilties, and alter cross entropy to recieve them. As we know, optimizing based on the logs achieves the same optimization, and is often more computationally effective.
22
Q
What is a good default approach to randomly initializing the weights and baises of an NN?
A
Init biases to zero; this is just super common.
Weights: when choosing outgoing weights from a layer with n nodes, we sample weights from a normal distribution with mean zero and stddev 1/sqrt(n)
The general idea is to have the weights inversely proportional to the # of nodes in the previous layer, and thus inversely proportional to the number of weights.
Intuitively, we can say that by doing it proportionally to the number of nodes that are feeding into the next layer, the inputs to the next layer aren’t too big or small, and they aren’t really dependant on the # of weights. But this is super hand-wavey, so I feel fine basically just saying “experimentally, this works really well.”
23
Q
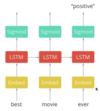
What are word embeddings?
A
A set of word embeddings is a mapping from each word in your vocabulary to a vector of a fixed length, say 768 (much shorter than your vocab size), where each word’s embedding contains meaningful information about the word’s meaning, its grammatical function, its relationship to other words, etc.
24
Q
What is one potential danger of word embeddings?
A
Retaining the biases of the training data. For example, the embedding for “homemaker” might be closer to “woman” than “man”. Debiasing strategies become important for this reason.
25
What are 2 big advantages of using word embeddings over just the one-hot encodings of the words?
1. It significantly reduces the dimensionality. Training is inefficient with one-hot because, if the input vector has one 1 and thousands of zeros, very few weights are lit up and thus are optimized per input.
2. They learn semantically meaningful information. They learn that "sandwich" and "hoagie" are similar, so the learning from one can immediately apply to another. That's better than having to relearn similar weights coming out of the node for sandwich and the node for hoagie.
26
*Generally* speaking, how are word embeddings learned?
In an unsupervised way, from a large and general text corpus like the set of all wikipedia articles.
27
What are 2 different ways word embeddings could be included in an NN, and how would each scenario work computationally and during training?
1: Each word is mapped to its pre-learned embedding using a key-value lookup table, and that is fed to the NN rather than the word itself. This key-value lookup is the first layer in the NN.
2: Custom word embeddings are learned as part of the NN you're training (maybe using an initialization via transfer learning or maybe not). So the start of your network would be a sub-architecture creating the word embeddings instead of just a lookup table.
28
What is the general heuristic of the word-2-vec algorithm for word embeddings? Which words does it want to have similar embeddings?
The algorithm assumes **words that often have similar contexts are similar, and thus should have similar embeddings.**
29
What is a super fun example of doing arithmatic in the vector space of word embeddings?
King - Man + Woman = Queen :D
30
I'm not gonna record the nuts and bolts of the algorithms that learn word-2-vec embeddings, but what is the super general idea of the two algorithms you can use?
One is to use a word to predict its context, and one is to use a word's context to predict that word.
31
What is the general idea of attention in an NN?
The computer pays attention to the relevant parts of the inputs at each step of learning or prediction. For example, in image classification, just looking at the pixels that contain the phenomena of interest, or in language translation, looking at the relevant words before writing the next word in your translation.
This method is big for seq-to-seq tasks like language translation.
32
Encoder/decoder architectures have been used to learn information from one source and translate it to another source. For example, an encoder CNN might understand an image, and the decoder RNN will write a text description of it.
But commonly, the encoder and decoder are both RNNs, for tasks like language translation. How does this traditional architecture work, and what is one big drawback?
The encoder RNN iterates over the input, updating its hidden state at every time step. Then the final hidden state of the encoder RNN is passed to the decoder RNN, which iteratively create the translated sentence one word at a time.
The big drawback is **the decoder only has access to the *final* hidden state of the encoder RNN**, so it only has access to what that final state was "thinking about". Even if it's an LSTM, maybe the long-term memory is only thinking about a certain portion of the input when we reach the end, and not thinking about the whole thing, for example. It's just gonna be difficult for the encoder to learn to communicate *all* the necessary information about the input to the decoder.
33
How does attention work, at a high level, for an encoder-decoder where both are RNNs?
The encoder passes *all* of its hidden states, from every time step, to the decoder, rather than just the last one. This is great: the decoder has access to a hidden state for each individual part of the input, so it can sort of understand all parts of the input equally well.
Then, at each time step in the decoder (i.e. at each word it's trying to produce), it focuses on the most important parts of the input. It learns parameters during training that figure out which parts of an input are important to focus on based on what part of the output it's trying to produce.
It does this basically by learning to, at a given time step, assign each of the encoder's hidden state a weight based on how important it is, and then it calculates a "context vector" which is just the weighted sum of all the encoder's hidden states.
I'm not gonna get more in the weeds than that.
34
What is an example of when the decoder would need to have attention on more than one word in the input/encoder? Say for example we're translating from English to Spanish?
Say we're translating the sentence "I throw the ball." In English, the conjugation "throw" can be used for the subject "I", "we", or "they".
But in Spanish, each of these has a unique conjugation. So when writing the word "throw" in Spanish, the decoder can't just look at the corresponding word "throw" in English; it also has to look at the subject of the sentence, so it knows how to conjugate in Spanish.
35
How might attention be used if the encoder is interpreting an image, and the decoder is writing a text description of that image?
The decoder figures out where in the image is relevant to the particular part of the description it's currently writing. *Awesome.*
36
Do you use dropout during evaluation, or just training?
Just training.
This makes some intuitive sense: if you had regularization as a part of your objective function rather than through dropout, you would want to penalize the model for complex weights during training, but when examining the validation set you really just wanna see how good your predictions are regardless of how complex the model parameters are. So I suppose the analog is also true for dropout.
37
Greyscale images are stored with pixels between 0 and 255. What preprocessing step is basically always done, and why is it helpful for learning?
Normalizing the input, as usual! Subtract mean, divide by std dev. (There are some tricks to quickly approximate this process that probably aren't important rn.)
This way, the network is recieving a standardized distribution of pixel values regardless of the input image, which helps training. Otherwise dim images vs bright images would be hard to treat similarly, for example.
38
What are 3 advantages to using a CNN for computer vision as opposed to a normal MLP?
1. Fewer parameters: the same set of parameters are applied again and again, making the network more simple and probably decreasing overfitting.
2. Because it's using the same weights in different places, learning from one place can be applied elsewhere. A bird will look the same in the top right vs bottom left; with an MLP the network would have to re-learn that in every location on the network, but the CNN can learn it once and apply elsewhere. In that way it's like an RNN: a word means the same thing at the beginning or end of a sentence.
3. Because we're using a square convolution, it uses spacial information more intuitively and much better than an MLP, which would recieve the input flattened into one long vector presented one row of pixels at a time.
39
How does a convolutional layer work in its most basic form? Say we have a square input greyscale image, and we're applying a single convolution to it with dimension 3x3. How would the next layer be calculated?
The convolutional layer is going to have a convolution, or 'filter', which is a 3x3 array of learned weights. To perform a convolution, you apply it to a part of the grid by multiplying the pixel values by the corresponding weight, then summing the results, and then passing the sum through an activation function.
You do that for all parts of the image (depending on stride and padding and such, but ignore that for now): you scan across the image continually applying the convolution to form the output of the layer, which is still square.
40
If you're trying to have an application of the convolution centered at every pixel in the input image, handling the edges gets weird: with a 3x3 convolution, if you're on an edge, there will be parts of the image with no input pixel to multiply?
What are three ways this can be handled? What is the most common?
I'm pretty sure the most common is padding. It feels common.
41
How are color images, or 'RGB' images, represented as numerical input to a CNN? How does this compare to a greyscale image?
Say a greyscale image is 28x28 pixels. It is represented by a 28x28 grid of scalar values between 0 and 255, denoting brightness at a given pixel.
RGB images need to keep track of not just one color (and not just one "brightness level"), but three: red, green and blue. So it is represented by *three* 28x28 grids of scalar values between 0 and 255, with one pertaining to the "red brightness", one to blue, and one to green.
So the greyscale image is represented as a (28,28) matrix. The RGB is a (28,28,3) matrix: **it has three**"**channels", and is referred to as having a "depth" of 3**: its width and height are 28, and its depth is 3.
42
What is a convolution's stride?
The amount of pixels it moves at a time. If it's one, it scans one pixel at a time. If it's 2, it skips every other pixel. And so on.
43
Suppose we're using a 3x3 kernel, a stride of 1, and we haven't padded or extended the image. If the input is NxN, what size will the output be?
What if it's instead a 5x5 kernel?
3x3: On every side of the image, there will be one row/column that we can't apply the kernel to, so each side decreases in size by 2. The output is (N-2)x(N-2)
5x5: now each size loses 3 rows, so it's (N-4)x(N-4)
44
Suppose we've padded an image such that, with a stride of 1, the output image will be the same size as the input.
If the stride is 2, what size will the output be?
If the input is NxN, it'll become (N/2)x(Nx2), because for every row and column, a pixel is only being formed in the output for every other pixel in the input.
45
How is a convolution applied to an RGB image? What shape would the filter be, and how would the resulting output be calculated?
An RGB image has 3 channels, so its shape is something like (28,28,3).
In a normal 28x28 image, we'd have a filter like a 5x5 array of weights, and we'd apply it at a point by multiplying the weights by the corresponding pixels, summing all the resulting numbers, and passing through an activation.
The RGB case is similar, except now the filter is 5x5x3. The height and width can be whatever, but **the depth of the kernel will equal the depth of the image, so we can learn about each of the input channels.** This way we basically have three 5x5 kernels being applied to the image: one to the red values, one to blue, and one to green. Then all 5x5x3=75 results are added together, across all 3 channels, and then passed through an activation function.
So conceptually, an edge detector could learn how to detect edges separately in each of the 3 colors, having one detector for each color. For example.
Below is a *great* image.
46
Suppose an input is of shape (28x28x3) (as with an RGB input image), and we want the output of our convolutional layer to be of size (28x28x4). Don't get bogged down with getting the output 28x28 part right, and focus on the 4.
How would this work? Describe what weights the convolutional layer has, and how it applies them to get the output with a depth of 4.
Say we use a 5x5x3 filter, and we pad the image such that with a stride of 1, the outcome will be 28x28x\_. What will the depth be?
Well we scan the width and height of the image, and at each point we apply our "three separate 5x5 filters" to the three channels, sum the 75 outputs across all 3 channels into one scalar, and pass through activation. So we’re getting one scalar at each point. That means the output is depth 1: 28x28x1.
So how do we get 28x28x4? **We learn 4 *different, separate* 5x5x3 filters**. Each will result in its own 28x28x1 output, yielding a 28x28x4 output.
47
Why would we want to have a convolutional layer whose output depth is higher than 1? Why would we wanna have, say, 5 different 5x5x3 filters to apply to a 28x28x3 RGB image, so the output dimension is 28x28x5?
Each filter can learn something different about the input! Maybe one detects edges, one records how bright it is, one checks if the dominant color is red, etc. Or maybe they just all detect *different* types of edges. One filter can only really learn one thing, but using multiple allows us to learn more complex and varied information during each layer.
48
We've learned that, to apply a convolution to an RGB input, we need a filter of a shape like (5x5x3): the depth then corresponds to the three color channels.
What if we're later in the CNN, and the input channel is like (128,128,25). How would we make a filter for that?
Something like (5x5x25)! Whether it's an input layer or not, all we need is for the depth in the kernel to match the depth of the input, so we can apply a 2d filter to each of the channels, and learn about all the channels.
49
Suppose an input of shape (N,N,32) enters a convolutional layer, and we want an output of (N,N,45). Without getting hung up on the first two dimensions, what filters does the conv layer need in order to make this happen.
It needs 45 different filters of a shape like 5x5x32. Each filter's depth needs to match the depth of the input so it can look at all the channels in the input, and each filter will produce one NxNx1 output, so we need as many filters as we want output channels.
50
What is the high-level purpose of a max pooling layer
Decrease the height and width dimensions of the tensor, so weights don't explode as we slowly increase channels.
51
How do max pooling layers work? How would a 2x2 max pooling layer be applied to, say, a 28x28x3 input, and what would the output size be?
How does the less common average pooling layer do this?
A 2x2 max pooling layer will decrease the height and width of an input by half, so the output will be 14x14x3.
It does this simply enough by, within each channel, looking at each 2x2 grid within the channel, and outputting the max of those 4 values.
An average pooling layer does the exact same thing, but instead of outputting the max of the 4 numbers, it outputs their mean.
52
Why would you want to use a max pooling layer? What is the benefit of decreasing the width and height of the channels at certain points in your network?
Often, we want to apply many filters to a given layer, meaning the outputs of our convolutional layers can be very large and require many parameters, which could lead to overfitting. For example, say we’re applying 1000 filters; that will add up fast.
If we decrease the height and width by 2 every so often, we can offset this growing of the parameters: as we increase depth, we can decrease height and width.
53
Can a CNN be trained on inputs of different sizes?
Generally no. You would think they could, because you just take the filter and continually slide it over the input regardless of size, but the issue the size of the activation matrix would continue to be different throughout the network, and eventually you'd typically flatten the matrix into a 1d vector that you pass to a normal dense layer; but dense layers can only take inputs matching their exact length. So you need the same sized images.
(I suppose you could get away with it if all you use is conv and pooling layers, and at the end your loss function can be applied to a variable-size output.)
(Future Drew here: I suppose this could be one thing global pooling layers are for?)
54
What would be a common construction for a CNN being used for a task like image classification. How would the layers be ordered, and what would happen to the input over time?
To start the network, there would be several blocks of one or more convolutional layers followed by a max pooling layer. Each blocks' convolutional layers will typically use padding so the height and width of the image don't change, and thus they only change when the max pooling layers decrease them by half.
We will continually learn more and more 'features', or 'channels', about the input as we go, so when combined with the max pooling layers decreasing width and height, we will go from a representation whose height and width is much larger than its depth, to the other way around: a very deep representation with small width and depth.
After we achieve this through several conv-pooling blocks, we'll flatten the resulting matrix out into a 1d vector, and pass it through a few simple dense layers before outputting our prediction.
The below image doesn't show the dense layers at the end.
55
What is reflected by the fact that our matrix is gaining more and more channels throughout the CNN?
We're learning more and more features/pieces of information about the input. And of course as we get deeper in the network, those features/insights become more complex, as they are supposed to with simple MLPs as well.
56
Generally, when instantiating a convolutional layer, what information do you need to tell pytorch about it?
The number of input channels, and the number of output channels
The height and width of one of the kernels (their depth will equal the number of input channels)
The stride and padding information
57
When instantiating a max pooling layer, what information do you need to tell pytorch about it?
Just the height/width and the stride
58
What is “groups” in a convolution? So if you have a normal Conv2d layer in pytorch and you set the flag groups=2 or 3, what does that mean, and what does it accomplish?
From pytorch docs: “At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels and producing half the output channels, and both subsequently concatenated.”
So yeah. Basically it's a way of decreasing the number of connections in a conv layer mapping in\_channels to out\_channels, by having each out channel only consider a subset of the input channels. The higher the groups, the fewer number of input channels being considered by a given output channel.
59
What are some good ways to augment your dataset of images? Why is this valuable?
You can apply a bunch of different rotations, zooms, crops, reflections, random noise, color distortion, etc to your input images, resulting in lots more slightly different images.
This just makes your CNN more robust to picking up the features of the image when those features are in different sizes, orientations, etc. If you're recognizing cats, this helps you identify big cats, small cats, cats on their sides, upside-down cats, etc.
60
When using a large pre-trained model for transfer learning, what two factors most impact the extent to which you'll want to retrain or structurally alter the existing model?
1. **The size of your dataset:** the smaller it is, the less capable you are of retraining a gigantic network.
2. **The quality of the match between their task and yours**: if your image classification task is super similar to theirs, you need less retraining or structural alteration than otherwise. It's easier to move from dogs to wolves than from dogs to cancer detection.
61
Why is transfer learning so prevalent in computer vision tasks like image classification?
There are already giant, well-trained networks that can classify wide arrays of images, like ImageNet. These can often be slightly reworked to transfer all that big-data learning to your small-data task, or the parameter initizations can serve as a great starting point before fine-tuning if you have enough data to do so.
(Ah how times change. NLP too now!)
62
Say you're doing transfer learning, using a big pretrained image classifier for some image classification task of your own. What might be a sensible way to handle it if:
1. You have little data, and it is similar to their task?
2. You have lots of data, and it is similar to their task?
3. You have little data, and the tasks are not similar?
4. You have lots of data, and the tasks are not similar?
**Little and similar**: you can use most of the layers and can't do much retraining, so maybe just replace a couple of the fully connected layers at the end, leaving all the layers before it fixed and not backpropogating through them
**Lots and similar:** because you have lots of data, you should still fine-tune the architecture, but the parameters learned from the similar task are a good initialization. You'll of course swap out a layer or two at the end (as with any of these cases) just so your # of output classes is correct
**Little and not similar:** Here, overfitting to our small dataset is still an issue, so we will hold the parameters from the original network as constant. But now because the datasets are different, task-specific features that the original network learns in later layers will not be useful. We can, however, still use the more abstract features from earlier layers, like textures and edge detection. So we remove most of the original layers, leaving only the beginning layers that extract more general image features. Then we add a few new layers and only backpropogate through the new ones.
**Lots and not similar**: you might fine-tune the parameters from the original, or you might just totally retrain it and just use the original network's hyperparameters, like number and size of layers, as a starting place.
63
How do autoencoders work? What task are they trying to accomplish, and what architecture do they use to accomplish it? What is the loss function?
Autoencoders are a compression algorithm, or a learned means of dimension-reducing an input, then scaling it back up to its original size with as little lost information as possible.
An autoencoder is basically a neural network made up of two sub-neural-networks: the encoder and the decoder. The encoder takes the input and maps it to a low-dimensional representation, and the decoder takes that low-dimensional representation and maps it back up to the original size of the image.
That low-dimensional representation in the middle there is the compressed form, and the goal of the network is to get that as good as possible. The loss function is simply to compare the input to the reconstructed input: if the input was an image, you just find the pixel-level MSE between the two, so the network aims to make the output as similar to the input as it can.
64
What are a few applications of autoencoders:
Compression obviously: one computer could store the trained encoder, and the other could store the trained decode, and then they can send the low-dimensional representations from one to another.
Denoising, which is so goddamn cool and shown below. By just storing the most "semantically meaningful" information about the input, you can drive away meaningless noise, which is good for denoising.
Similarly, image reconstruction: if a little sliver of an image is missing, an autoencoder can fill it in
65
Without getting into the weeds (I'm not concerned with the lowest-level math), how do transpose convolutional layers, or "deconvolutional layers", generally work, and what are two potential applications?
In autoencoders, the decoder needs to take a low-dimensional vector and **upsample it into an image**. Similarly, in a GAN generating images, then generator needs to take a small vector of noise and upsample it into an image.
These networks start to look like reverse CNNs: CNNs slowly go from large height/width and few channels to small height/width and many channels.
So these upsampling networks need to do the opposite, slowly increasing the height and width. This is what reverse convolutional layers do: they **basically apply a filter which is larger than the area it's being applied to, and doing so with a high stride like 2, so the output height and width are larger than the input's.**
66
What is a global average pooling layer? How does it work, where might you include it in a CNN, and what purpose does it serve.
A GAP layer, if included, would be included after all the blocks of conv/pooling layers, before the fully connected layers.
It is basically an extreme version of a pooling layer: it maps every channel to one scalar, which is the mean of all the values in the channel.
Often, the inputs to the dense layers are so large (so many channels of substantive height and width), that there are just too many parameters in the final dense layers, which can cause issues with overfitting. This is a way to combat that overfitting: it drastically decreases the size of the input to the dense layers, thus decreasing the number of parameters they need to have.
Because of the nature of conv layers vs dense layers, oftentimes most of a network's parameters can be in those final few dense layers, so this can be a very effective way to decrease the # of params and combat overfitting.
67
What are 2 big CNNs that can be used for transfer learning?
VGG19, ResNet (eh don't worry about memorizing this)
68
We've already covered that momentum can be used to "power through" local minima in order to hopefully reach other minima that are lower.
What is another potential advantage of using momentum during gradient descent? In what situations will this advantage be present, and how will momentum achieve this?
Because it takes an average of all previous gradients, with a focus on recent gradients, it can smooth out learning if it happens to be jagged. If the gradients keep jumping back and forth in one of the dimensions, those will average out to about zero, and the descent will stop taking big steps in those dimensions and focus on the dimensions with a consistent direction.
This is illustrated in the following picture. These are contour lines, and each line is at a constant level in the z direction with respect to itself. So this means the slopes are way more steep in the y direction than x, because height is changing over a much smaller horizontal distance. This may be easier to see if you envision it as maximizing over a hill rather than minimizing over a valley.
So in this context, you can see (in blue) how the baseline slopes will be much larger in the y direction than x, causing most of each step to be a jagged movement in the y direction rather than a productive movement in the more subtle x direction. Momentum (in red) smoothes this out. (The red drawing over-exaggerates the size of the steps in that direction, but it’s just meant to illustrate how the jagged y-direction movement is decreased.)
69
How are RMSProp and AdaGrad related?
They're basically the same thing, RMSProp is just an optimized version. They can be discussed and conceptualized very similary
Source: https://towardsdatascience.com/a-visual-explanation-of-gradient-descent-methods-momentum-adagrad-rmsprop-adam-f898b102325c
70
What is the goal of the RMSprop optimization algorithm, and how does it work *intuitively?*
The goal, similar to momentum, is to combat jagged and inefficient learning by smoothing out our steps in the direction of the gradient.
The general idea of RMSprop is it keeps track of which dimensions keep having large steps and which keep having small ones, and uses that information to smooth out training by decreasing the relative size of the large ones and increasing the relative size of the small ones.
It does this by dividing the size of the step in each direction by a weighted average of recent derivatives in that direction.
71
How does RMSprop work at a lower level?
Again, the goal, similar to momentum, is to combat jagged and inefficient learning by smoothing out our steps in the direction of the gradient.
In momentum, you keep a exponentially decaying weighted average of the gradients, and each iteration you take a step in the direction of that weighted average.
In RMSprop, you instead keep an exponentially weighted average of the squares of each of the partial derivatives, and then to construct the “gradient” which is the direction you want to move, for each dimension you take the current partial derivative, and divide it by the square root of the exponentially decaying sum of the derivatives.
That’s pretty complicated, but here’s the intuition: because we’re squaring the derivatives in the sum, they’re always positive; so **the bigger the past derivatives, the bigger the value by which we’re *dividing* the size of our current step.** Steep dimensions where learning is jagged will have large gradients, so we’ll be dividing by a large value and decreasing the size of the step; conversely, not-steep dimensions with slow learning will now have relatively larger steps, so we make proportionally more progress in that direction. This can be used to increase the learning rate, and overall learn faster.
The key parts of this picture are the **top**, showing the image where each fault line has a consistent height and thus the y axis is much steeper, and the **bottom**, showing how the update is the derivative, divided by sqrt(weighted sum of squares of derivatives).
72
As of a few years ago at least, what is the "best" optimization algorithm, in the sense that it's consistently very effective across a wide array of deep learning applications?
Adam
73
What is a quick, one-sentence summary of the adam optimization algorithm
It takes momentum and RMSprop and puts them together.
(These are both effective means of smoothing out training and making it more consistently move in the right direction in a non-jagged fashion, so this is a good idea!)
74
Expand a little more on how the adam optimizer works
Adam combines momentum and RMSprop.
So, ignoring an optimization or two that isn't that important for conceptual understanding, basically what you do is:
Keep track of an exponentially weighted sum of the past gradients (for momentum), as well as an exponentially weighted sum of the *squares* of the past gradients (for RMSprop)
Then your update at a given time step will be the current exponentially weighted sum of the gradients (as with momentum) *divided by* the square root of the weighted sum of the squares of the gradients (as with RMSprop).
75
What are the key hyperparameters of the adam optimizer?
Learning rate, the size of the step. Obviously important and need to be tuned.
Then there is Beta1, which determine the rate at which the exponentially weighted sum of the gradients drops off (i.e. how quickly old values disappear towards zero), and Beta2, which is the same thing for the weighted sum of the squares of gradients used in RMSprop.
Beta1 and Beta2 are more commonly not messed with and just left to the default values.
76
Off the top of your head: what are GANs, and how do they work?
A GAN, or generative adversarial network, is a model essentially composed of two separate neural networks: a generator and a discriminator.
The generator recieves as input a vector of random noise and transforms it into a generated fake member of a dataset; for example, maybe it turns it into a picture of a face. The discriminator recieves either a real member of a dataset, or a fake one made by the generator, and it predicts the probability that the input is real.
To train this joint network, the generator tries to maximize the discriminator's predictions on its fake inputs, and the discriminator tries to minimize those predictions and maximize predictions on the real inputs. Hence adversarial.
77
What are a few things GANs can be used for?
Creating new data, or new fake members of a dataset, such as images or videos
Transferring aspects of a dataset onto another: making a video of a horse look like a zebra, making a photo in the style of a certain artist, turning a rough sketch of an object into a much more detailed sketch, deep fakes, etc
78
What are the approximate 5 steps in the lifecycle of creating a deployed ML model
1. Get the data
2. Clean and explore it in preparation for modeling
3. Train/validate a model
4. Deploy it
5. *Monitor and update it*: check the input data doesn't drift too much, and that predictions remain good, etc
79
What is batch normalization in neural networks? What is the intuition behind why it's useful?
Applying batch normalization to a layer simply means normalizing the layer’s outputs to have mean 0 and std 1, by subtracting the batch mean and dividing by the batch variance. So we’re normalizing with respect to the current batch, not the whole dataset.
So similar to how we normalize the inputs to a model, we can also normalize the inputs to layer n+1 by applying batch normalization to layer n.
It’s helpful to normalize some layers within the NN, not just normalize the inputs, because in the same way that the consistency of inputs to a network helps it learn, consistent inputs to any given layer help it learn more easily, quickly, and consistently. Any layer can be thought of as “the input layer in the remaining sub-network”, and having consistent inputs to that sub-network will be helpful!
80
How is batch normalization implemented?
Basically how it's explained: subtract the batch's mean and divide by its variance.
The only deviation from this is that we actually add a small epsilon to the variance in practice. This is partially to avoid a variance of zero, and partially because we’re really trying to estimate overall population variance, which is typically a little higher than a batch’s variance.
81
What is the primary benefit of batch normalization, and what is a possible secondary benefit?
The primary purpose and benefit of batch norm is faster training (which could potentially allow for more complex models, or smaller learning rates, etc). A possible secondary benefit is thus that maybe we can get better accuracies.
There are lots of other potential small benefits (very light regularization, potentially allowing for a wider range of activations, weight initializations are less important, can help with vanishing gradients) that probably aren't as key.
82
What is the xgboost library at a very high level?
The xgboost library is an ML library for training models that are ensembles of decision trees using gradient boosting. The implementation in the library contains many optimizations, making it very fast and effective, hence it's popularity throughout the ML world.
Creating models with xgboost is simple: its interface is very similar to sklearn for example.
It was made by CMU professor Tianqi Chen!
83
How does the gradient boosting algorithm work for decision trees, as with xgboost?
Boosting is of course a technique for training an ensemble model where each model is trained sequentially, and models try specifically to correct the errors of past models.
As a first note on xgboost specifically: rather than each model predicting a probability if we're doing classification, or predicting the actual outcome if we're doing regression, each tree predicts an arbitrary scalar score. So whether we're doing classification or regression, the output of a single tree is an arbitrary scalar in (-inf,inf). Then for either, the prediction of the overall model is the ***sum*** of the scalars for all these trees, rather than the average. The rest of the solution builds on summing rather than averaging.
Then in gradient boosting specifically, **tree i tries to predict the negative of the residual of the model formed by trees 0 to i-1.**
An intuitive explanation of why this works is basically model i is trying to predict for itself the residual of the composite model formed by models 0 to n-1, and then model i outputs the negative of that residual to correct it and make the predicted residual zero. In other words, model i is, intuitively, trying to predict the shared error of all previous models so that it can correct it. **I don't know why the word 'gradient' is present.**
All that might not be 100% surgically accurate in all cases, but I do think it captures the big ideas of how the implementation works and the intuition behind it.
Anything beyond that is pretty complicated, and hopefully not necessary.
https: //machinelearningmastery.com/gentle-introduction-xgboost-applied-machine-learning/
https: //xgboost.readthedocs.io/en/latest/tutorials/model.html
84
What is the gamma parameter in xgboost?
The gamma parameter is a pseudo-regularization tool for xgboost. It represents the minimum amount of reduction in loss that is required for a node in a decision tree to do a certain split. So if a split doesn't help enough, it won't happen.
Normal regularization adds a penalty to the optimization function based on the model's complexity, whereas this parameter simply stops expanding the model if the expansion isn't helpful enough. They both achieve similar goals of limiting model complexity to hopefully combat overfitting.
There do exist actual regularization terms for the models, but they seem to be less commonly used, perhaps because gamma is intuitive whereas regularizing a weirdly-parameterized decision tree model is not.
85
What are two great reasons to choose xgboost?
It can handle NaNs, which is extremely useful and something NNs can't do
It has lots of explainability and feature-importance tooling you can quickly use to get a sense of what's going on
86
What is a transformer layer essentially?
A transformer layer is basically just a layer which applies self attention to an input sequence, plus some additional frills for performance.
So it receives some sort of embedding of every input in a sequence, and uses self attention to output new, better embeddings for that sequence.
87
At a high level, how does the transformers computation work? How are the input words (for example) transformed into contextual embeddings via self attention?
You'd typically operate on a batch of sequences, but say for simplicity you're just using one sequence X, and say for simplicity each entry in the time series has an embedding of just length 1. So X is just a row vector of length k. (These concepts of course expand to batches and multidimensional embeddings.)
You first alter X trivially to give K Q and V, which can all just be thought of conceptually as "the original input data."
You take K and Q and rework/multiply them (through a simple outer product I suppose) to get a kxk matrix, where k is the length of the sequence. Then you pass that through a row-wise softmax. This output kxk matrix gives **a normalized weighting of how important each other other word.**
Then you multiply that by v to get a weighted sum of all the words for each of the words.
88
Why is BERT important for the NLP community?
Of course because it achieves state-of-the-art results on many NLP tasks that use a language model, but also because it *makes transfer learning for NLP very easy*, similar to how it has been in the past for computer vision. BERT is a big, downloadable pre-trained model trained on gigantic sets of data (all of Wikipedia or something like that), and you can leverage that general understanding of the english language to make great task-specific word embeddings, sentence embeddings, or whatever, *without having tons of data yourself.*
89
What is BERT generally?
BERT is a language model that takes as input a phrase and returns context-dependent word embeddings for each of the words, as well as a context-dependent embedding for start and end tokens which are placed at the beginning and end of the word. ("Context dependant word embeddings" is how I think about it.) "Base" embeddings are size 768; "large" embeddings are size 1024.
"Context dependent" meaning, for example, the embedding for 'trump' will be different if it's in "Donald Trump" vs if it's in "I'll trump you."
BERT is a technology based on transformers and self-attention.
90
How in general might BERT use the concepts of attention, and specifically self-attention?
When trying to find a context-dependent embedding for a particular word in the input phrase, it will figure out what other words in the phrase it should have its attention on based on which are relevant to this word. It's self attention because it's referencing within the original input sequence, rather than in say machine translation where you're keeping attention on places in the input phrase while creating a word in the output phrase.
This is how it uses context. Say you're embedding the word "blue": in the phrase "the blue sky" you might your attention on 'sky', but in the phrase "I feel blue" you'll probably focus on the word feel, and get a very different embedding that reflects the different meaning of the word in the new context.
Another example is "coreference resolution": in the phrase "I saw James and threw the ball to him", when you're embedding the word 'him', the model will hopefully have attention on the word James because it's figuring out what 'him' refers to.
91
Suppose they asked me to explain BERT in a bit of depth: how would I go about responding?
Something like "I know that BERT essentially creates context-dependent word embeddings for each word in an input phrase, as well as for additional start and end tokens, and this is in part based on self attention...expand a bit on self attention...
but it's been well over a year since I really needed to think about BERT as something other than a black box that creates good sentence embeddings, so I haven't studied up on transformers and such much recently and can't speak much to them. I'll be taking advanced NLP coursework this year though, so I'm excited to refresh myself!
I'm also familiar with how BERT's outputs an be used to create sentence embeddings, useful for tasks like classification...
92
How does SBERT generally work? How does it relate to BERT, and how can it go from word embeddings to sentence embeddings?
SBERT is essentially a fine-tuned version of BERT that pools word embeddings to create good sentence embeddings.
For a given input phrase, BERT's output is an embedding for each word, and the start and end tokens. These can be "pooled" to make sentence embeddings: one common option is simply to output the embedding of the start token as your sentence embeddings, and another is to take the average of all the embeddings. SBERT automatically does one of these based on the version (so its output on a given phrase is a single sentence embedding vector), and it has been fine-tuned to be good at this specifically.
93
Different versions of SBERT can and have been trained using different methods, but what is one key method that has been used?
You have SBERT embed two sentences, then use something simple like cosine similarity to calculate the sentences' similarity based on the sentence embeddings, and then you compare this to a label you have between 0 and 1 showing how similar they are.
94
How could BERT be used to build a search engine?
Suppose we're using it for sentence/phrase/paragraph embeddings specifically, getting it from the embedding of the start token.
We can use this for search engines: get an embedding of the text from every page on the internet, and get an embedding for the phrase the user input to the search engine, and return pages whose embeddings are similar to the query's embeddings
95
How could BERT be used to make a classifier like a spam filter or a fact-checker?
Input your documents to BERT and get a sentence embedding for each, then train a few additional layers to predict your outcome variable based on those embeddings. If you have lots of data you could also fine-tune BERT itself.
96
What's the spirit of momentum learned in convex optimization?
We want to speed up training, and to increase learning rate to do so (maybe even beyond what we can theoretically guarantee will converge). But we can't just wantonly increase leraning rate, or learning becomes jagged and bad.
So we essentially **adaptively use a different learning rate based on the "terrain".** In jagged areas the **learning rate ends up being low, in effect** (because when we sum past gradients, they're not similar and cancel each other out, decreasing the effective learning rate).
In smooth ares, the summed gradients instead synergize, **effectively increasing the learning rate.**
So it's basically a form of adaptive learning rate tuning!
97
How do normalization and batch normalization work? Do they find an average for each particular neuron, or a certain dimension, or the whole tensor?
For both, I think the general answer is that there are different ways of doing it.
The general idea of normalization is you want all of the outputs from a particular layer to follow the same (unit normal) distribution, so that the same learning rate can be effectively applied to all outputs. Out of this comes the fact that the most theoretically correct way to do normalization is to find the mean and stdev for every neuron, and normalize them all the same, so they're all output with the same distribution. (See DeepLearningAI's normalization youtube video.)
That said, this is not always what people do in practice. Empirically, dumber/less theoretically sensible things can work fine. For example, at Aurora, we normalized our images using just a single mean and stdev calculated across the whole tensor and the whole dataset, because that was simple and sufficient. Some people even go simpler and just divide an mnist image by 255, for example.
There are also intermediate solutions, where you pick a particular dimension and calculate a mean and stdev for each of those dimensions, then use the same summary stats for every neuron that's part of the same entry in that particular dimension.
So for example, take the BatchNorm2d layer in pytorch, which normalizes a batch of CxHxW image representations (so input is NxCxHxW). Based on this layer's description, I'm pretty sure for a given batch, it computes summary statistics for each channel, then uses the same stats for each entry in a given channel.
98
What is the spirit of how adagrad works, as learned in convex optimization?
Maybe your objective function is way steeper in one dimension than in others. In this case (as well as in similar cases where some dimensions are out of whack), it'd be great to scale your gradient on an entry-by-entry basis, where take the big gradients and chill them out a bit, or take the tiny gradients and amp them up a bit.
This is what adagrad does: it stores historical gradient info, looks at which entries are recently usually really big or small, and uses that to
**You'll notice that this is very similar to what momentum does!** They're two different ways of accomplishing a similar conceptual goal, it seems.
99
Name an application that would use a many-to-many, many-to-one, and one-to-many RNN architecture
many-to-many: language translation
many-to-one: sentiment analysis
one-to-many: text generation with a starting word as a seed
100
There are 2 big reasons you wouldn't want to use a normal NN for text inputs, and RNNs solve them. What are they?
The input text is variable length, but normal NNs have an input layer of fixed length
A normal NN would learn different weights for the beginning and end of the sentence, even though there can be shared info (similar to a CNN): the phrase "Harry Potter" is a name whether it's at the start or end of a sentence.
101
How does a basic one-layer RNN work? What 3 sets of weights are learned, and how are they applied to an input?
An RNN has a **common "structure" or "hidden layer"** that is applied sequentially to each time step in the input structure; for example, words in a sentence.
At each application, there are basically 2 things that determine the activations 's' of the hidden layer: the input, and the weight matrix Wx that connects the input to the hidden layer; and **the activations of the previous application of the hidden layer**, and the weight matrix Ws that connects the previous activations to the hidden layer. The two matrix-vector products are calculated, summed, and passed through the activation function.
Then, a third matrix is learned which connects the activations of the hidden layer to the output layer. (Then maybe there's an activation like sigmoid.) Depending on the architecture, this might be evaluated at every step, or at just the last step, etc.
Here are 3 different ways of showing the same basic network; the first shows the key formulas.
102
In what sense does an RNN have "memory", and why is it useful?
RNNs use the activations of the previous layer to figure out the activations of the current layer. This is useful for using context: if the last two words were "throw the", the next word might be "ball"; if yesterday's stock price was high, odds are it'll be high today too.
103
What can we learn from the Elman Network representation of an RNN to better understand how information flows through the network? In what sense can Wx and Ws be thought of as one matrix? I just love this representation, it's so intuitive and actually explains the architecture: remember it!
In an RNN, both the input vector x and the previous activation vector s are multiplied by their own respective weight matrices to get new vectors of the same length, which are summed to get the final value. This is where the formula activation([Wx]\*x + [Ws]s\_t-1) comes from.
But this is not actually that weird, because it can just be thought of as x and s\_t-1 being lined up into one vector and multiplied by one weight matrix!
104
How would an RNN have "multiple layers", such as if it had 3 layers?
If you're confused, think about it in the Elman diagram way again.
It's pretty intuitive: the first layer recieves the input and the first-layer activation from the previous iteration. Similarly, the nth layer at time step *t* recieves the activation of the n-1st layer at time *t*, and the activation of the nth layer at time *t-1*.
Sometimes each layer has the same weight matrix, except specific ones for the first input and last output. Other times it's different and there's fewer shared matrices.
105
What is the algorithm called to optimize an RNN?
Backpropogation through time
106
What is an intuitive explanation of backpropogation through time?
We need to update 3 weight matrices: Wy, Ws, and Wx. So we need to find the derivative of the loss function with respect to each matrix (or the derivative w.r.t ecah of the parameters within each matrix).
Because some matrices are called more than once in the **chain of dependencies**, we need to go back in time and encorporate all of those calls.
The key is the chain of dependencies. So if we're looking at the loss function at time step 3, the y matrix Wy (which connects the hidden layer to the output) only has one invocation in this particular dependency chain for this time step, so the computation is easy. But if we're looking at Ws or Wx, each of those was used at 3 separate times in the past, so we need to find the derivative factoring in each of those invocations using the chain rule.
107
How is an RNN optimized using backpropogation through time?
Specifically, say an RNN with length-n input has a length-n output. For a single input x, how is each weight matrix updated based on that output and its parts?
How is this different if there's just one output at the end, as with sentiment analysis?
(I'm *pretty sure* the following is true)
If a single input has n outputs, that's basically n instances where the loss function can be calculated and backpropogation can occur.
So if there's 3 outputs, the first output will be used to update Ws based on one invocation; the second output will again be used to update Ws based on 2 invocations; and the 3rd uses 3 invocations. And similarly for Wx; Wy always only has 1 relevant invocation in the chain of dependencies.
This makes sense: if we have n outputs, such as if we're labeling POS for the words in a sentence, we basically have n unique predictions, so even if it's just one input in a sense, we have n opportunities to learn and improve our predictions.
Now I'm sure that, rather than updating the weights after each of these, you could instead accumulate the gradients, average them, and then make an "aggregate update", similar to how with batch gradient descent you store a few individual-point gradients, average them, and take a step.
108
What is a big problem with normal RNNs? How does it happen, why is it bad, and how can it be combatted?
Vanishing gradients lead to "bad long-term memory". Basically, when we're trying to update Wx or Ws based on the output at a very late time step, we find the derivative of the contribution of that matrix W from all previous time steps.
But the derivative for early time steps is a *lot* of derivatives chained together, leading to vanishing gradients. So when we're updating based on a late outcome, the contribution of an earlier part of the input vanishes. This can be bad: words at the beginning of a sentence can have a big impact on the meaning of the end of the sentence, for example.
It's intuitive that vanishing gradients are especially bad for RNNs: they're bad when a bunch of layers are applied in a row, because all of the potentially small gradients are getting multiplied together. Well, an RNN has a layer that can easily be applied 50 or 100+ times if the input x has 100+ time steps.
The solution is LSTMs
109
RNNs also suffer from exploding gradients. What is a simple and effective way of combatting this?
"Gradient clipping": just penalize the network for creating gradients above a certain threshold
110
At a high level, what new functionality do LSTMs add on top of normal RNNs?
Long term memory! RNNs have a mechanism for using short term memory, but due to the vanishing gradients problem, they can't really effectively retain info from very long ago. LSTMs add a path to pass along and retain long term memory in addition to the short term memory pathway.
I'm not gonna get into memorizing gates and architecture and stuff; as Dr. Kolter said, a lot of that is hand waving. There are 4 "gates" for bringing in and interpreting old and new information, and reforming it into new long and short term memories.
111
Where does the output/prediction of an LSTM cell come from, if applicable
It is based only on the newly updated short term memory vector, which is multiplied by another matrix to generate that output value just like in normal RNNs.
112
What is the general idea of LSTM cells that use peephole connections?
The peephole connections basically allow the cell to make more heavy use of the previous LTM by inserting it into more locations.
113
What is an example of a sentence where long term memory would be important for understanding a later part of the sentence?
Perhaps, for example, there is a verb late in the sentence, and the subject of that verb came way earlier in the sentence.
“**The cat**, which already ate at about 4pm and quite enjoyed their wet food, **was full.**”
114
GRUs are kind of a variant of LSTMs. How do they work at a high level?
GRUs only have one memory vector flowing through, rather two for a separate LTM and STM, as with LSTMs. In this way, they look much more similar to normal NNs.
But unlike normal RNNs (which basically only have one simple gate that passes the concatenated input-and-previous-activation through 1 layer of an NN), GRUs have 2 gates. These gates work to decide which "memory cells" in the previous cell's activation should be overridden with new information, and which should be retained as a sort of long term memory. This allows the system to learn to maintain certain pieces of information for an arbitrary period of time.
If you think GRUs are gonna be important to understand, you could rewatch the coursera video on them to better understand how they work and make updates at a low level.
115
What are two potential uses of an RNN which, at every step t, tries to predict the next value in the sequence, X\_t+1?
Writing new text, either one word at a time or one letter
Time series prediction: predicting stock prices or something
116
If you're training an RNN whose prediction at time step t is "what's the value of the input at time t+1", how do you construct the outcome variable? Why does this construction avoid letting the RNN use the outcome variable when predicting the outcome variable?
You construct the outcome variable as you would intuitively: you just shift the input over by one and have that be the outcome variable
The reason this isn't "cheating" is **for this type of RNN task, we're just using a feed-forward RNN rather than a bidirectional RNN**. So at any given time step t, the only information available to the RNN to make predictions is the inputs at time steps t and earlier. So there's no cheating
The RNN is evaluated sequentially. So it makes the t=1 prediction, then a gradient is found; then it does t=2, and gets another gradient; and so on
117
Can you use dropout in RNNs?
Yep! It works for any of the relevant weight matrices.
118
If you're making an RNN over a sequence of letters to predict the next letter in the sequence, what *exactly* is the prediction output?
What about if you're predicting at the word level?
A probability distribution showing the odds it's a given letter, or a given word in your vocabulary. Depending on your application, you could then grab the highest probability word/letter, or sample from the distribution output by your network.
119
How are word embeddings included in an RNN?
You put the word embedding layer(s) between the input and the "main RNN cell", so from the perspective of the cell, the embedding *is* the input. If you're learning a custom embedding scheme while training the RNN, you can have backprop-through-time go through the embedding layer.
(In this picture sigmoid just refers to an FC layer with a sigmoid activation)
120
In feed-forward RNNs, when making the hidden state and prediction for a given time step, we only have access to the input at that time step and earlier time steps.
What is an example of a case where we would also want information on the following part of the sentence? Say in named entity recognition (identifying which words in a sentence are names)?
In "I got you a movie about Teddy bears," Teddy isn't a name
But in "I got you a movie about Teddy Roosevelt," Teddy is a name
121
What type of RNN allows us to look at later parts of the input when calculating the hidden state and prediction at an earlier timestep?
Bidirectional RNNs
122
How does a bidirectional RNN (or LSTM or whatever) work for an example task like named entity recognition?
It's pretty simple: there are basically "2 RNNs", one that iterates over the input from front to back, and another that goes from back to front. So 2 hidden states are learned for each input: one that uses that input and all the earlier context, and another that uses that input and all the later context. Then both of those hidden states are concatenated and passed through a single dense layer to get the prediction, which in this case is the probability that a word is a name.
